改进布谷鸟算法在结构可靠性分析中的应用
秦 强,冯蕴雯,薛小锋
(西北工业大学航空学院,陕西西安710072)
改进布谷鸟算法在结构可靠性分析中的应用
秦 强,冯蕴雯,薛小锋
(西北工业大学航空学院,陕西西安710072)
在计算过程中,标准布谷鸟算法(cuckoo search algorithm,CS)中的参数是保持不变的,这影响了该算法的收敛性和计算精度。为了克服这一缺陷,首先探讨了标准CS中飞行步长和淘汰概率两个关键参数的变化规律对该算法全局搜索与局部搜索能力的影响,然后对这两个参数进行了自适应改进,同时,提出了一个具有全局最优导向的搜索方程以进一步提高CS的局部搜索能力和收敛速度。利用改进后的CS与人工神经网络响应面法相结合进行结构可靠性分析。算例分析说明,与标准CS以及粒子群算法和遗传算法相比,所提出的改进CS在进行结构可靠性分析中,能够有效地减少计算时间并提高解的精度。
改进布谷鸟算法;人工神经网络;响应面法;结构可靠性
0 引 言
在结构可靠性分析中,常采用Monte-Carlo法、一次二阶矩法、二次二阶矩法等方法计算结构失效概率。其中,Monte-Carlo法需要足够多的模拟次数才能得到结构的失效概率,因此该方法效率较低;而一次二阶矩法和二次二阶矩法都需要求解结构极限状态方程对随机变量的偏导数,且对于非线性程度较高或有多个局部最小值的极限状态方程,这两种方法可能导致错误的结果[1]。由于智能优化算法,如遗传算法(genetic algorithm,GA)和粒子群优化算法(particle swarm optimization,PSO)等在求解结构可靠度指标时,不需要求解结构极限状态方程对输入变量的偏导数,并且有全局寻优的特点而被应用到结构可靠性分析中[1-3]。
文献[4]根据布谷鸟特殊的寄宿式产蛋行为抽象得出的布谷鸟(cuckoo search algorithm,CS)算法具有全局寻优性能强、路径搜索方式特殊、控制参数较少等优点,使得该算法的计算效率与求解精度优于GA与PSO等智能优化算法[5-6]。文献[7- 8]将CS算法成功地应用到许多工程和结构优化问题中。文献[9- 10]对标准CS算法进行改进,将最优解之间的信息交换加入到CS中,并对Lévy飞行中的随机步长的大小提出了改进以加强局部搜索能力,该改进算法能够在多数测试函数中比标准CS算法、PSO算法、差分进化算法得到更优的解。文献[11- 12]通过改进的CS算法解决了系统可靠性冗余分配问题,其中文献[11]对CS算法中的Lévy飞行步长和鸟窝被发现概率pa引入自适应机制,文献[12]使用GA算法优化CS算法中的参数,以提高标准CS算法的全局及局部搜索能力。另外,对于复杂结构来说,其极限状态方程一般为隐式函数,此时,响应面法常被用来将隐式功能函数显式化。其中,应用较为广泛的是多项式函数响应面法,但随着输入变量增加,该方法的计算量大大增加[1314]。文献[15]的对比分析结果表明,在结构可靠性分析中,神经网络响应面法的效率和精度都要高于多项式响应面法。
为了提高结构可靠性分析的效率和精度,本文将影响标准CS算法收敛性和计算精度的两个参数进行改进,同时又提出了一个改进的搜索方程以进一步提高CS算法的收敛速度。本文将改进后的CS算法具有计算精度高、收敛性快以及神经网络能够非常好的逼近结构极限状态方程的优点相结合,提出了一种新的结构可靠性分析方法。该方法不仅提高了标准CS算法在结构可靠性分析迭代过程中的计算速度,并克服了迭代过程后期计算精度较差的缺点。本文对于改进CS算法中参数变化规律的原理分析及算例分析充分说明了所提方法在计算结构可靠度时的优越性。
1 改进的CS算法
1.1 标准CS算法及缺陷
与一般鸟类繁殖方式不同,布谷鸟采用寄生产卵的方式繁衍其下一代,它们将自己的蛋存放到其他鸟类的鸟窝中,让其他鸟类为其孵化。当其他的鸟类发现其窝里有外来的蛋,则会将外来的蛋丢弃或放弃自己的窝,然后另选它处搭建新的鸟窝。文献[6]根据布谷鸟这种寄宿式繁殖策略抽象出CS算法,并规定了3个理想假设:
假设1 每只布谷鸟一次只产一个鸟蛋,且随机选择一个鸟窝来存放该鸟蛋。
假设2 含有高质量鸟蛋的最好鸟窝将会保留至下一代。
假设3 可用的鸟窝数量n是不变的,外来鸟蛋以概率pa∈[0,1]被寄主鸟窝的主人发现。

在上述3个理想假设的基础上,CS算法中布谷鸟寻找最优鸟窝的更新公式为式中,x(g)i表示在第g代中的第i个解;α是步长控制量;L(λ)为服从Lévy概率分布的随机搜索路径;⊕为点对点乘法。每次迭代产生新的鸟窝后,将布谷鸟所产鸟蛋被寄主发现的概率pa与随机产生的[0,1]区间的随机数r进行比对,若pa<r,则对x(g+1)i进行随机改变,反之不变,公式为式中与表示第g代的两个随机解,更新后的鸟窝位置仍记为

在标准CS算法中,外来鸟蛋被寄主发现的概率pa与步长控制量α是两个非常重要的参数,一般是固定值,在迭代过程中保持数值不变,在文献[6]中,取pa=0.25,α=1。在迭代寻优过程中,如果pa一直较大,α较小,会加快标准CS算法收敛速度,但付出的代价是可能无法得到高精度全局最优解;而如果α较大,pa较小,会导致寻优的迭代次数明显增加[11]。标准CS算法根据Lévy飞行进行搜索的方向和距离都具有高度的随机性,能轻易地从当前搜索区域跳出而对另一区域进行搜索,使得标准CS算法具有非常强大的全局寻优能力[17]。然而利用Lévy飞行机制进行寻优不能充分地发掘和利用更多局部区域的信息,致使标准CS算法在每个鸟窝周围无法进行完全和认真仔细的寻优,这主要是该算法所表现出来的高度随机跳跃性,导致其局部搜索能力较差。
1.2 改进的布谷鸟算法
针对标准CS算法局部搜索能力较弱这一缺陷,本节提出改进的布谷鸟(improved cuckoo search,ICS)算法首先将对标准CS算法中的重要参数:鸟蛋被发现概率pa与步长控制量α进行自适应改变。优化前期,为了搜索更多的区域以提高算法的全局寻优性能,pa与α应取较大值。随着寻优计算的进行,算法会收敛到全局最优解附近,此时α与pa应逐渐减小,使算法在该区域附近进行寻优以得到高精度的解且加快收敛速度[17]。然而在迭代过程中,pa与α的下降速率却不相同,在迭代的早期,应在足够多的迭代步骤中保持pa有一个较大值,这样可以增加算法中解的多样性,但在迭代后期,各鸟窝会聚集在全局最优解附近,此时pa应取较小的数值以保证算法的收敛;而对于飞行步长α,其变化趋势应与pa有所不同,这主要是因为在迭代计算早期,α取较大值有利于跳出局部最优解,但在迭代后期,α保持在一个较小值,有利于对局部区域进行仔细搜索,以增强求解的精度。由上述思想归纳出的pa与α随迭代次数g变化的计算公式为

式中,N表示最大迭代次数;发现概率pa的最大值与最小值分别以pa,max、pa,mim表示;步长控制量α的最大与最小值分别以αmax、αmin表示,且都在CS算法中pa与α默认值的附近取值,取pa,max=0.5,pa,min=0.1,αmax=1.5,αmin=0.5;m1、m2为非线性因子,取值大于0,用来控制pa与α的下降速率。由式(3)可以得知,当m1和m2均为1时,表示pa与α这两个参数呈线性下降趋势,然而为了使pa在迭代的早期保持较大值,且α在迭代早期下降较快但在后期保持一个较小值,m1应小于1,相反,m2应大于1,m1越小,pa就会在越多的迭代步骤中取较大的值,直接导致计算用时的增加,而m2越大,α则只能在越小的前期迭代步骤中取得较大值,在更多的迭代后期步骤中保持较小值,可能会导致计算陷入局部最优解,这就削弱了算法在全局搜索能力与局部搜索能力之间的平衡关系。所以,在选取非线性因子时,m1不宜太小,且m2不应过大,本文取m1=0.5,m2=3。假定总的迭代次数N=1 000,pa与α随迭代次数变化曲线如图1所示。

图1 pa与α随迭代次数变化曲线
从图1可以看出,pa在迭代的早期下降较慢,在迭代次数达到800步时,pa仍大于标准CS算法中的默认值0.25,但在迭代后期,迅速降至最小值;而α在迭代早期有一个随着迭代次数增加而明显减小的趋势,当迭代次数超过200后,α已经小于1,且在迭代后期其值基本保持在最小值αmin。
另外,为了进一步提高算法的局部搜索能力和收敛速度,受PSO算法的启发,在ICS算法中对式(2)进行了修改,得
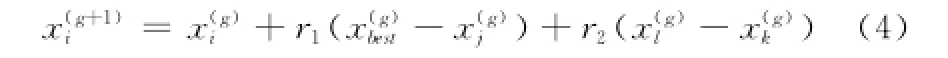
式中,r1和r2为[0,1]区间的随机数为第g代中所有鸟窝中的最优解和分别表示第g代的3个随机解,且j≠k≠l。当r1或r2大于pa时,对进行改变。与式(2)相比,式(4)增加了最优鸟窝引导布谷鸟算法寻优的搜索项,从而大大提高算法的收敛速度。如果说式(2)是基于随机策略的搜索方程,那么式(4)是基于精英策略的搜索方程,在生成新解时用到了当前解中的最优信息。
2 利用神经网络生成极限状态方程
当对复杂结构进行可靠性分析时,需要通过复杂的数学方法(如有限元法)计算结构的响应,这个过程相当耗时。为了提高可靠性分析的效率,许多学者利用神经网络响应面法将结构极限状态方程显式化[23,1214]。
在用神经网络响应面法近似结构极限状态方程的过程中,首先应经过尽量少的确定性试验得到结构的响应,然后将结构的受载、结构形状等参数作为神经网络的输入数据,将确定性试验得到的结构响应作为输出数据,组成训练样本集,同时,为了避免因各数据量级之间的差距过大而导致得不到精确的神经网络的情况出现,应将训练样本进行归一化处理。然后构建神经网络结构,包括神经网层数、各层中的神经元数量以及各层之间的传递函数。最后,通过训练样本对神经网络进行训练,当网络误差满足精度要求后,便得到训练好的神经网络。通过各连接层之间的传递函数就可得到结构的响应与输入变量之间的函数关系,即得到结构的显式极限状态方程。
本文算例中所用的神经网络模型都只含有3层网络,即一个输入层,一个隐含层和一个输出层。其中输入层中的神经元数量和随机变量的个数相同,输出层都只有1个神经元,隐含层均有10个神经元,输入层到隐含层的传递函数为正切函数,隐含层到输出层的传递函数为线性函数。在生成训练样本集方面,通过在设计空间中对各变量随机生成200个样本作为输入数据,然后得到对应的结构响应作为输出数据,进而得到训练样本集。
3 利用本文所提方法进行结构可靠性分析
标准正态空间中,坐标原点到极限状态方程的最短距离称为可靠性指标β,所以在进行可靠性分析时,应将结构中的随机变量标准正态化并构造具有等式约束条件的极小值问题以求解结构可靠性指标β。
目标函数为

约束条件为

式中,x*
i(i=1,2,…,n)表示标准正态随机变量;xi(i=1,2,…,n)表示结构可靠度分析中的n个独立随机变量;μxi与σxi分别对应各随机变量的均值和标准差;g(X)=0表示结构的极限状态方程,在本文中该方程是通过神经网络响应面法计算得到。
求解式(5)和式(6)所表示的有约束的优化问题等同于采用罚函数法计算如式(7)所示的无约束优化问题[1]。

式中,λ为惩罚因子,是一个很大的正数,本文取λ=1010。得到式(7)后,将其作为适应度函数,通过ICS算法计算求得的该函数最小值就是结构可靠度指标β,进而得到结构的失效概率。在用ICS算法与神经网络对结构进行可靠性分析时,主要有以下几个步骤:
步骤1 建立神经网络的训练样本集和测试样本集,根据神经网络响应面法得到结构的显式极限状态方程g(X)=0。
步骤2 通过罚函数法得到结构可靠性指标β关于随机变量的目标函数,如式(7)所示。
步骤3 设置CS算法的参数,并对鸟窝进行初始化,即得到设计空间中随机变量的初始值。
步骤4 根据式(1)和式(4)对鸟窝位置进行更新,并对新的鸟窝和当前鸟窝进行适应度函数评价。如果新的鸟窝适应度要好于当前鸟窝适应度,则将新的鸟窝替换掉当前鸟窝,否则按照一定的概率pa抛弃部分鸟窝,然后按照Lévy飞行产生新的鸟窝。
步骤5 重复步骤4,直到迭代次数达到最大迭代数N时,寻优结束。
值得注意的是,在对以上步骤进行结构可靠性分析的过程中,pa与α的值按照式(3)不断变化。利用ICS算法与神经网络响应面进行结构可靠性分析的流程图如图2所示。

图2 利用本文所提方法进行结构可靠性分析流程图
4 算例分析
为了验证本文所提方法在解决结构可靠性问题中的计算效率和计算精度,通过采用GA算法、PSO算法、CS算法和ICS算法对两个经典结构可靠性分析算例和一个工程算例分别进行对比分析。在计算过程中,各种算法均独立运行20次,每次运行中的最大迭代次数N为1 000次,且GA算法、PSO算法和CS算法中的参数都选取其默认值,种群数量均为25。在计算结果中,β表示可靠性指标,βmin、βmax和βavg分别表示β的最小值、最大值和平均值,Pf为失效概率。
算例1 极限状态方程

式中,x1与x2为相互独立的正态变量,x1~N(1 000,2002),x2~N(250,37.52)。利用重要抽样法求得此极限状态方程失效概率的精确解为0.009 607[3]。该算例计算结果表1所示。
由表1可以看出,4种计算方法均能得到该极限状态方程失效概率较为精确的计算结果。在计算误差方面,GA算法的误差最大,而PSO的计算结果要优于GA得到的计算结果,但是PSO需要更长的计算时间来得到计算结果,其计算时间基本是GA的两倍;CS与ICS在计算用时与计算误差两个方面都要优于前两种方法,尤其是在计算用时方面有了显著提高,不仅ICS的计算时间略小于CS的计算用时,而且ICS的计算误差要小于CS的计算误差。在对可靠性指标β进行求解的20次独立的寻优迭代过程中,虽然CS在收敛精度方面虽优于前两种算法,但要比ICS差,而ICS每次都会收敛到最小值。通过该算例说明了ICS算法具有良好的寻优能力。

表1 算例1计算结果
算例2 考虑多变量极限状态方程g(X)=x1+x2-x3-x4+6,随机变量均服从标准正态分布。利用一次二阶矩法求得该极限状态方程可靠性指标的精确解为3.0[16],对应的失效概率约为1.350×10-3。该算例计算结果如表2所示。
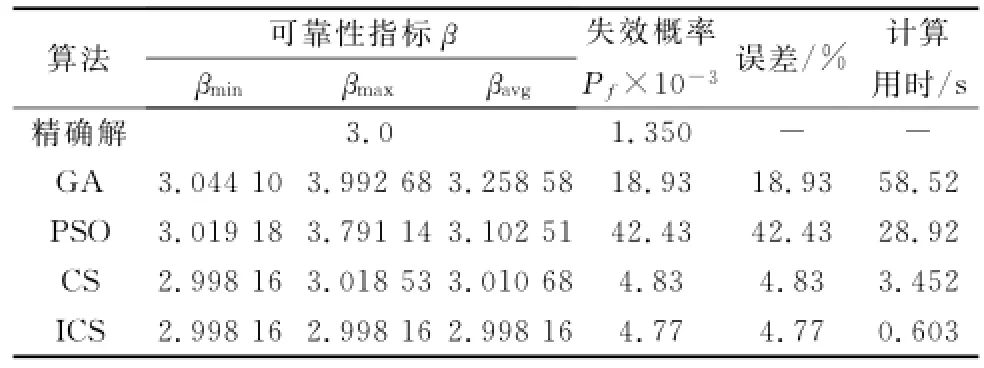
表2 算例2计算结果
从表2的计算结果可以看出,对于多变量极限状态方程,CS算法和ICS算法可以得到非常精确的解,而GA与PSO虽然计算得到的可靠性指标的平均值βavg与精确解之间的相对误差分别为8.620%和3.417%,但其对应的失效概率的误差分别是58.527%和28.926%,可见该误差是相当大的。另外,在计算用时方面,4种计算方法得到的结果与算例1中各方法计算用时的规律一致,其中PSO的用时最长,ICS用时最短。同样,在每次的迭代过程中,ICS均可得到非常精确的解。此算例说明,在进行具有多变量的结构可靠性分析中,ICS算法依然表现出非常出色的计算能力。
算例3 本文所提方法的工程应用取某型飞机货舱门锁钩为例,所研究的锁钩结构的有限元模型如图3所示。在飞机飞行过程中,该锁钩承受飞机机舱内的增压载荷,锁钩受力F,锁钩材料的弹性模量E、锁钩的宽度L以及锁钩的内圈半径R为基本随机变量。锁钩静强度可靠性分析的极限状态方程为g(X)=σb-σmax(X)=0,式中,σb为材料的拉伸强度极限;σmax(X)为锁钩承受的最大应力,其是F、E、L和R等随机变量的函数。以ANSYS workbench作为锁钩接头最大应力的分析工具,且各随机变量的取值和分布形式如表3所示。

图3 锁钩有限元网格模型

表3 算例3中随机变量参数
本例中采用108个样本对训练好的神经网络进行Monte-Carlo抽样计算,并将该方法计算得到的结果作为精确解,但Monte-Carlo法耗时太大,且与文中提到的4种智能算法不具有可比性,所以不考虑该方法的计算用时。用不同方法计算得到的结果如表4所示。
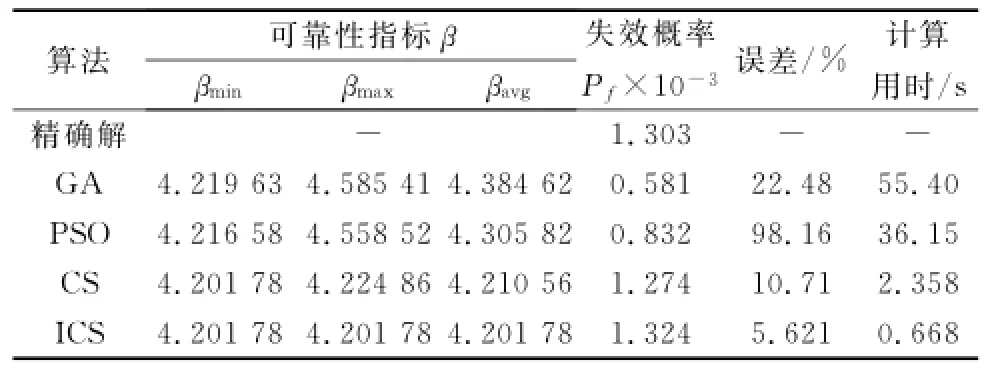
表4 算例3计算结果
通过表4的结果可知,通过Monte-Carlo法得到的某型飞机舱门锁钩的静强度失效概率为1.302 8×10-5,对应的可靠性指标β=4.205 45。虽然由GA算法与PSO算法计算得到的可靠性指标的平均值βavg与精确解之间的相对误差分别为4.260%和2.387%,说明这两种算法在求解该问题时也可以得到较为精确的解,但其对应的失效概率的误差分别达到了55.408%和36.151%,这是因为可靠性指标β在此范围的较小变化都会导致对应的失效概率有非常大的差别,较大的失效概率误差是不可接受的。而ICS算法的计算精度与计算时间要明显优于CS算法,失效概率的误差仅为0.668%,再次充分说明本文所提ICS算法在解决工程结构可靠性问题中能够得到相当精确的可靠性指标值,且在计算时间上具有明显的优势。
5 结 论
(1)针对标准CS算法中两个重要参数在迭代计算过程中保持不变会导致该算法具有较低的计算效率和计算精度这一缺陷,提出了一种针对参数随迭代次数变化的改进策略,然后将一种改进的搜索方程引入到标准CS算法中,减少了算法的计算时间。
(2)ICS算法分别将鸟窝发现概率和飞行步长作了不同的变化策略,进而能够更加合理地平衡标准CS算法的全局和局部搜索能力,提高算法的计算精度和收敛速度。
(3)文中对CS算法参数的解析分析以及算例对比结果均表明,本文所提出的ICS算法对结构可靠度的计算更为准确,且计算效率更高。
[1]Charles E.Structural reliability assessment based on particles swarm optimization[J].Structural Safety,2005,27(10):171- 186.
[2]Cheng J.Hybrid genetic algorithms for structural reliability analysis[J].Computers and Structures,2007,85(19/20):1524 -1533.
[3]Cheng J,Li Q S.Reliability analysis of structures using artificial neural network based genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering.2008,197(45/48):3742- 3750.
[4]Yang X S,Deb S.Cuckoo search via lévy flights[C]∥Proc.of the World Congress on Nature&Biologically Inspired Computing,2009:210- 214.
[5]Rajabioun R.Cuckoo optimization algorithm[J].Applied Soft Computing,2011,11(8):5508- 5518.
[6]Yang X S,Deb S.Engineering optimisation by cuckoo search[J].International Journal of Mathematical Modeling and Numerical Optimisation,2010,1(4):330- 343.
[7]Yang X S,Deb S.Multi-objective cuckoo search for design optimization[J].Computers and Operations Research,2013,40(6):1616- 1624.
[8]Gandomi A H,Yang X S,Alavi A H.Cuckoo search algorithm:a metaheuristic approach to solve structural optimization problems[J].Engineering with Computers,2013,29(2):17- 25.
[9]Walton S,Hassan O,Morgan K,et al.Modified cuckoo search:a new gradient free optimisation algorithm[J].Chaos,Solitons and Fractals,2011,44(9):710- 718.
[10]Zhang Y W,Wang L,Wu Q D.Modified adaptive cuckoo search algorithm and formal description for global optimization[J].International Journal of Computer Applications in Technology,2012,44(2):73- 79.
[11]Valian E,Tavakoli S,Mohanna S,et al.Improved cuckoo search for reliability optimization problems[J].Computers and Industrial Engineering,2013,64(1):459- 468.
[12]Kanagaraj G,Ponnambalam S G,Jawahar N.A hybrid cuckoo search and genetic algorithm for reliability redundancy allocation problems[J].Computers and Industrial Engineering,2013,66(4):1115- 1124.
[13]Deng J,Gu D S,Li X B,et al.Structural reliability analysis for implicit performance functions using artificial neural network[J].Structural Safety,2005,27(1):25- 48.
[14]Elhewy A H,Mesbahi E,Pu Y.Reliability analysis of struc-tures using neural network method[J].Probabilistic Engineering Mechanics,2006,21(1):44- 53.
[15]Cheng J,Li Q S,Xiao R C.A new artificial neural networkbased response surface method for structural reliability analysis[J].Probabilistic Engineering Mechanics,2008,23(1):51- 63.
[16]Tan X H,Bi W H,Hou X L,et al.Reliability analysis using radial basis function networks and support vector machines[J].Computers and Geotechnics,2011,38(2):178- 186.
[17]Qin Q,Feng Y W,Ye C.Reliability analysis of door locking based on improved cuckoo algorithm[J].Aeronautical Computing Technique,2014,44(1):23- 26.(秦强,冯蕴雯,叶忱,等.基于改进布谷鸟算法的舱门锁定可靠性分析[J].航空计算技术,2014,44(1):23- 26.)
Improved cuckoo search algorithm for structural reliability analysis
QIN Qiang,FENG Yun-wen,XUE Xiao-feng
(School ofAeronautics,Northwestern Polytechnical University,Xi’an 710072,China)
In the iterations,the parameters of standard cuckoo search algorithm(CS)are constant,which may affect the convergence and accuracy of the algorithm.To overcome this defection,the variations of the two main parameters which affect the global search and local search capabilities are investigated,and then improvements are made to the parameters.In addition,a modified search equation which aims to further improve the CS local search ability and convergence speed is proposed.The improved CScombined with artificial neural network respond surface method is proposed to solve the structural reliability problem.Comparison with the standard CS,particle swarm algorithm and genetic algorithm,the proposed improved CS reduces the computation and improves the accuracy of the solutions effectively in the process of structural reliability analysis.
improved cuckoo search algorithm(ICS);artificial neural network;respond surface;structural reliability
TH 115;TB 114.3
A
10.3969/j.issn.1001-506X.2015.04.40
秦 强(1986-),男,博士研究生,主要研究方向为飞行器结构机构可靠性与优化设计。E-mail:johnnystyle@126.com
1001-506X(2015)04-0979-06
2014- 07- 07;
2014- 09- 25;网络优先出版日期:2014- 11- 19。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141119.2225.010.html
国家自然科学基金(10577015);航空科学基金(2006ZD53050,2008ZA53006)资助课题
冯蕴雯(1968-),女,教授,博士,主要研究方向为飞行器结构机构可靠性与安全性分析。E-mail:fengyunwen@nwpu.edu.cn
薛小锋(1982-),男,讲师,博士,主要研究方向为航空航天可靠性工程。E-mail:xuexiaofeng@mail.nwpu.edu.cn

