基于参数估计与记分函数联合的直觉梯形模糊随机前景决策方法

陈振颂，熊升华，李延来，钱桂生

（1．西南交通大学交通运输与物流学院，四川成都610031；2．西南交通大学综合交通运输智能化国家地方联合工程实验室，四川成都610031；3．香港城市大学科学与工程学院系统工程与工程管理系，香港999077）

基于参数估计与记分函数联合的直觉梯形模糊随机前景决策方法

陈振颂1，2，熊升华1，2，李延来1，2，钱桂生3

（1．西南交通大学交通运输与物流学院，四川成都610031；2．西南交通大学综合交通运输智能化国家地方联合工程实验室，四川成都610031；3．香港城市大学科学与工程学院系统工程与工程管理系，香港999077）

完善直觉梯形模糊数的算术运算，在直觉梯形模糊数及梯形模糊随机变量的基础上，定义直觉梯形模糊随机变量（instuitionistic trapezoidal fuzzy random variable，ITr FRV），探讨并证明ITr FRV的相关性质。针对具有ITr FRV且属性权重未知的模糊随机多属性决策问题，考虑决策者心理行为特征，提出基于参数估计与记分函数联合的直觉梯形模糊随机多属性决策前景决策方法。该方法首先获取决策子周期内的直觉梯形模糊样本信息，估计分布类型已知的直觉梯形模糊总体的未知参数，以获取直觉梯形模糊随机决策矩阵；其次，构造带有方差的期望直觉模糊数矩阵，定义模糊随机记分函数，将规范化的期望直觉模糊数矩阵转化为记分函数矩阵；最后，利用前景理论计算前景记分函数，进而基于灰色系统理论求解属性权重，获取综合前景记分值，由此进行方案比选。案例表明本文方法的可行性及有效性。

多属性决策；直觉梯形模糊随机变量；参数估计；记分函数；前景理论

0 引 言

复杂决策系统的不确定性通常分为模糊性和随机性两类，模糊性反映了决策者对于复杂系统往往缺乏充分的信息而无法给予精确性描述所造成的认知不确定，而随机性则源于事物本质的不确定及因果关系的不确切所导致的结果不确定［14］。随着决策系统（尤其是精密仪器、尖端设备等）的复杂性日益呈现几何级数增长的趋势，更为直观地考量是寻求能够同时刻画决策问题模糊性与随机性的决策方法，即模糊随机多属性决策方法（fuzzy random multi-attribute decision making，FRMADM）。结合对既有研究成果的分析［5-8］，可以发现针对模糊性与随机性并存的系统分析方法主要具有两类处理思想：①分别利用模糊变量及随机变量表征决策系统的模糊性与随机性，进而处理相应于模糊变量及相应于随机变量的决策信息，基于鲁棒性决策条件将模糊和随机不确定性传递至统一响应结构，进而集结决策结论；②考虑模糊性与随机性在同一多维整体内的合成表示，运用区别于灰色随机变量、二型模糊集、广义区间值二型模糊数等复杂信息特征数的模糊随机变量（fuzzy random variable，FRV）构建模糊性及随机性一体化的处理模式，根据FRV的相关性质衍生出众多决策方法。值得注意的是，上述两类处理方式各有所长，方式一将三维决策体系分割为模糊性及随机性相互独立的二维决策系统，鉴于现有模糊随机特征数的相关理论尚未完善，采用基于模糊数学和概率论与数理统计等相关学科成熟的理论基础，有利于避免模糊性信息与随机性信息集成处理过程中的信息丢失；方式二则融合了决策模糊性与随机性的特点，采用FRV直观表示模糊随机信息，虽然基于可信性理论的模糊随机变量理论体系尚待深入研究，但多数文献［9-11］的通行处理方式是将模糊随机信息转化为期望、方差及标准差等统计特征信息，进而依据前景理论、随机占优理论、期望—方差准则等定义判别准则或应用可能度、支持度、贴近度等概念获取决策结论，有效弱化了具有各类形式的模糊随机变量的处理复杂度。

事实上，目前针对属性值为FRV的多属性决策方法（multiple attribute decision making，MADM）研究较为少见，文献［12］较早提出FRMADM的概念，针对属性值具有区间数与随机变量等不同形式的情形，运用模糊随机模拟技术构造区间模糊随机变量，并利用简单加性加权（simple additive weight，SAW）算子集结相应于各方案的综合评估值，通过计算区间模糊随机变量的期望值获取方案排序。文献［13］考虑模糊随机环境下模糊随机期望值模型的求解问题，提出基于并行扰动随机逼近（simultaneous perturbation stochastic approximation，SPSA）算法的模糊随机模拟技术，利用模糊随机模糊技术估计FRV的期望值函数，并通过SPSA算法寻求最优解。文献［14］定义模糊随机有序加权平均（ordered weighted averaging operator，OWA）算子，通过计算各复合优度下的期望与方差，利用模糊随机模拟技术构建鲁棒模糊随机多属性决策模型。文献［15- 16］定义了区间概率模糊随机变量及其期望值与混合熵，提出基于区间概率模糊随机变量的期望值——混合熵的决策方法。并在后续研究中，针对属性值为区间直觉模糊数的随机多准则决策问题，定义离散型区间直觉随机变量，给出基于直觉模糊交叉熵的记分函数及记分期望值、记分标准差等概念，在获取方案的联合直觉随机变量分布及综合记分标准期望区间值的基础上，利用可能度方法确定方案排序。文献［17］针对属性权重未知、属性值为直觉模糊数的随机直觉MADM问题，定义离散直觉模糊随机变量，依据前景理论修正属性权重信息，采用简单概率加权方法获取综合集对记分函数值进行方案比选。从应用的角度来看，FRV作为不确定性环境下决策模型架构的基本工具，已广泛应用于模糊随机规划问题，文献［18］提出基于模糊算法的模糊随机线性规划模型，为测度两个FRV之间的线性相关程度，以模糊算法为基础构建模糊随机回归模型，定义响应FRV的决定系数为模糊随机相关系数，着重论证了其相关性质。文献［19］考虑库存管理决策问题，设定顾客年需要量为具有精确概率信息的离散模糊随机变量，以总库存成本最小化为目标建立模糊随机定期再购系统模型，确定了最优盘存时间、最优目标库存水平及最优交货期。此外，FRV在可靠性分析［20-21］、股票投资组合选择［22］、模糊随机更新过程［23-24］、模糊随机回归分析［25］等领域均得到了大量应用，无论是从方法上还是思想上均对FRMADM问题的解决具有重要的借鉴意义。

综上所述，国内外现有针对FRMADM的研究相对匮乏，但其应用前景却十分广阔，因此对其进一步深入探究极为必要。具体表现在以下几个方面：①有鉴于决策系统的复杂性，应利用刻画模糊性更强的模糊数构造FRV，以更为细腻地表达繁冗的决策信息；②针对属性值连续型FRV的MADM问题处理较为复杂的问题，绝大多数研究所考虑的均为属性值为离散型FRV的情况，因而需探索基于连续型FRV的简便、可行、有效的决策方法；③具有各类型模糊数的FRV的期望值计算通常可依据基于可信性理论的期望定义，然而对于含有直觉模糊数［26］的FRV期望值的获取必须在此基础上寻求新的方式；④一般而言，利用模糊随机模拟技术可以获取模糊随机总体分布的未知参数，但是该方法并不适用于解决具有直觉模糊信息的FRV的参数确定；⑤由于决策环境的不确定性，决策者往往无法获取决策所需的完备信息，加之自身的认知能力、逻辑推理能力有限，其决策行为往往表现为有限理性，因而决策结果往往偏离预期效用理论中的完全理性设想，达到“满意”而非“最优”。

为此，本文针对属性权重未知的直觉梯形模糊随机多属性决策问题，融合前述现有研究处理模糊性与随机性并存的两类决策思想，提出基于参数估计与记分函数联合的直觉梯形模糊随机前景决策方法。该方法针对丰富决策信息表达的需求，在直觉梯形模糊数和梯形模糊随机变量的基础上，定义直觉梯形模糊随机变量，更为细腻地刻画决策者认知不确定性；针对直觉梯形模糊随机变量的期望值计算公式，重新定义梯形模糊随机变量的期望与方差，在此基础上进一步定义标准直觉梯形模糊期望；针对模糊随机模拟技术的不适用性，基于直觉梯形模糊样本信息进行统计推断，获取参数的最大似然估计，以确定直觉梯形模糊总体信息；针对现有记分函数对于直觉梯形模糊随机变量不适用性，引入标准期望值对基于集对分析理论的记分函数进行适应性修正，定义模糊随机记分函数；针对决策者有限理性行为特征，引入前景理论描述决策者面对风险收益及损失的态度及敏感性差异。最后，案例分析结果表明本文方法的可行性和合理性。

1 直觉梯形模糊数及梯形模糊随机变量

1.1 直觉梯形模糊数及其运算规则

定义1［27-28］设X是一个非空集合，称为X上的一个直觉梯形模糊数，如果其隶属函数为

其非隶属函数为

针对直觉梯形模糊数的运算法则，文献［29］分析现有定义的缺陷及不足，给出一类新的算术运算，着重探讨新规则中基于期望加权的隶属度及非隶属度的合理性。在其研究基础上，文献［30］给出更加完善的直觉梯形模糊数的算术运算规则，本文将基于该运算规则展开讨论，其具体内容可参见此文献。

1.2 模糊变量及模糊随机变量

文献［31］为克服可能性测度［32］不具备自对偶性的缺陷而提出可信性理论（credibility theory，CT）以来，CT已然成为研究模糊现象的一个重要数学分支，广泛存在于不确定理论及其应用研究的各个领域。为此，首先给出可信性空间的定义，而后续模糊变量及模糊随机变量的相关定义正是以此为基石泛化衍生。

定义2［33］假设Θ为一个非空集合，P（Θ）代表Θ的幂集，Cr是可信性测度，则称三元组（Θ，P（Θ），Cr）为可信性空间。

定义3［33］设ξ为一个从可信性空间（Θ，P（Θ），Cr）到实数集的函数，则称ξ为一个模糊变量。

定义4［33］假定ξ是可信性空间（Θ，P（Θ），Cr）上的模糊变量，那么称

为模糊变量ξ的期望值，且式中两个积分至少一个有限（避免出现∞－∞的情形）。

定义5［33］假定（Ω，Σ，Pr）是一个概率空间，设ξ是一个从（Ω，Σ，Pr）到模糊变量集合的函数，并且对于R上的任何Borel集B，Pos｛ξ（ω）∈B｝是ω的可测函数，则称ξ为一个模糊随机变量。

定义6［33］假定ξ是概率空间（Ω，Σ，Pr）上一个模糊随机变量，则称

为模糊随机变量ξ的期望值。

1.3 梯形模糊随机变量

定义7［33］如果对于任意的ω，ξ（ω）＝［X（ω）－l1－l2，X（ω）－l2，X（ω），X（ω）＋l3］为一个梯形模糊变量，且该梯形模糊变量的隶属度函数满足

那么称ξ为一个梯形模糊随机变量。其中，l1＞0，l2＞0，l3＞0，X为一个实值随机变量。

针对梯形模糊变量ξ（ω），依据定义4可知，其期望为E［ξ（ω）］＝（4X（ω）－l1－2l2＋l3）／4，进而依据定义6，对于梯形模糊随机变量ξ，其期望为E［ξ］＝（4X－l1－2l2＋l3）／4。文献［33］进一步给出了梯形模糊随机变量ξ的方差定义。

定义8 设ξ为定义在概率空间（Ω，Σ，Pr）上的一个梯形模糊随机变量，且其期望E［ξ］有限，称

为梯形模糊随机变量ξ的方差。

定义8借鉴了经典概率论中关于方差的定义，然而，式（4）中的（ξ－E［ξ］）依旧是一个梯形模糊随机变量，因此不可避免地需要继续依据相应的梯形模糊数的运算规则进行计算，虽然确保了方差定义依然在模糊性框架之中，却无法有效利用统计学原理处理梯形模糊随机变量ξ中的随机性信息［34-35］。一般而言，对于一个梯形模糊随机变量而言，期望不仅代表了其模糊性信息的最可能性取值，也反馈了其随机性信息的最重要特征。因此，为避免应用梯形模糊数运算法则导致模糊随机统计信息的不一致性，利用其期望将模糊随机信息转化为含有方差的精确信息，进而探讨其相关统计特征与性质便可实现应用成熟的统计学方法协同处理。

在实际决策环境中，决策方法的可行性极为关键，通过处理决策者所提供的模糊随机信息获取相关特征数，能较大程度上降低算法复杂度及决策成本，并有效提升决策结论的精确性。因此，本文在梯形模糊随机变量的期望与方差的定义7及定义8的基础上，参考文献［36］，重新定义了梯形模糊随机变量期望，并进一步得到方差的适应性修正。

定理1［36］假定ξ是概率空间（Ω，Σ，Pr）上一个梯形模糊随机变量，则E［ξ］＝E（E［ξ（ω）］）。

定义9 设ξ为概率空间（Ω，Σ，Pr）上的梯形模糊随机变量，称

为梯形模糊随机变量ξ的期望。

定义10 设ξ为概率空间（Ω，Σ，Pr）上的梯形模糊随机变量，且其期望值E［ξ］有限，称

为梯形模糊随机变量ξ的方差。

2 直觉梯形模糊随机变量及其统计特征与性质

为了满足有效解决复杂决策问题的需要，本文在直觉梯形模糊数及梯形模糊随机变量的基础上，定义直觉梯形模糊随机变量，给出其几何直观并分析其部分统计特征及性质，为二维特征的繁冗决策信息的简洁表达提供一类新的途径。

定义11 如果对于任意的ω，ξ（ωi）＝［X（ωi）－l1－l2，X（ωi）－l2，X（ωi），X（ωi）＋l3；μξ（ωi），υξ（ωi）］为一个直觉梯形模糊变量，且该直觉梯形模糊变量的隶属度函数为

其非隶属度函数为

那么称ξ为一个直觉梯形模糊随机变量。

其中，μξ（ω），υξ（ω）分别为ξ（ω）的隶属度与非隶属度，πξ（ω）＝1－μξ（ω）－υξ（ω）为ξ（ω）的犹豫度，μξ（ω），υξ（ω），πξ（ω）∈［0，1］，c＞0、d＞0，X为一个实值随机变量。

事实上，若忽略对隶属度及非隶属度的限制，则直觉梯形模糊随机变量即退化为梯形模糊随机变量；对于确定的一个ω，直觉梯形模糊随机变量即退化为直觉梯形模糊数。针对直觉梯形模糊随机变量，图1和图2分别给出了连续型及离散型直觉梯形模糊随机变量的几何直观表示。

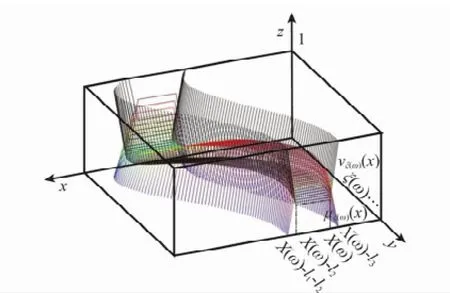
图1 连续型直觉梯形模糊随机变量

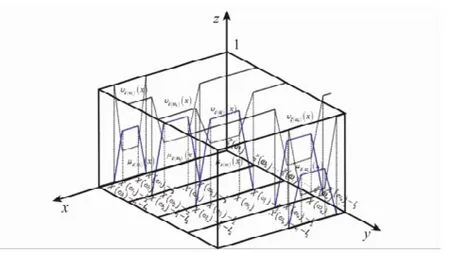
图2 离散型直觉梯形模糊随机变量

对于属性值为直觉梯形模糊随机变量形式的FRMADM问题，通常无法直接获取决策者针对各方案下不同属性的模糊随机变量信息，在具有一定周期的决策过程中，受时间限制及人力成本等因素的影响，仅能要求决策者提供数次以直觉梯形模糊数表征的决策评估样本信息。考虑样本的二重性，利用ξ（ω1），ξ（ω2），…，ξ（ωn）表示一组样本观测值，并将决策信息的获取过程假定为简单随机抽样［37］。类似数理统计中统计量的定义，下面给出部分直觉梯形模糊随机统计量的定义，并探讨其相关性质。

定义12 设一组取自某直觉梯形模糊总体的样本ξ（ωi），其中ξ（ωi）＝［X（ωi）－l1－l2，X（ωi）－l2，X（ωi），X（ωi）＋l3；μξ（ωi），υξ（ωi）］，ωi∈Θ（i＝1，2，…，n），Θ为参数空间，且各X（ωi）相互独立，则样本均值为

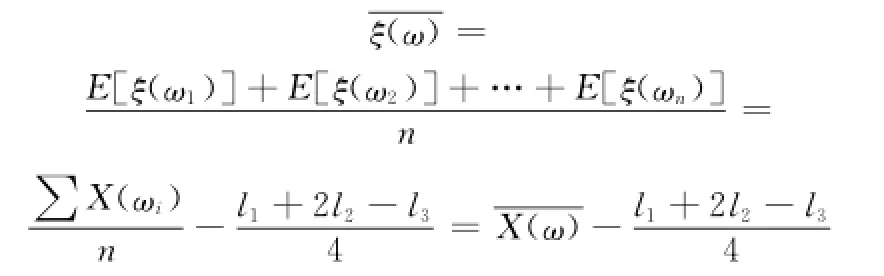
其隶属度均值为

非隶属度均值为

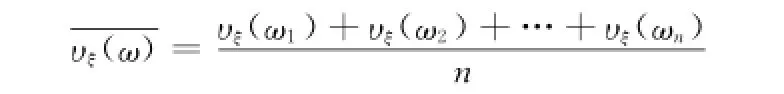
定义13 设一组取自某直觉梯形模糊总体的样本ξ（ωi），其中ξ（ωi）＝［X（ωi）－l1－l2，X（ωi）－l2，X（ωi），X（ωi）＋l3；μξ（ωi），υξ（ωi）］，ωi∈Θ（i＝1，2，…，n），Θ为参数空间，其样本均值为称

为直觉梯形模糊偏差，并分别定义

为隶属度偏差、非隶属度偏差以及犹豫度偏差。

其中

事实上，直觉梯形模糊随机变量的隶属度、非隶属度以及犹豫度即为一般实值随机变量，其相关性质在此不予以赘述。以下主要针对直觉梯形模糊随机变量的样本均值及样本方差的定义，探讨并证明其部分性质。

定理2 设D［ξ（ωi）］（i＝1，2，…，n）为相应于一组取自某直觉梯形模糊总体的样本ξ（ωi）（i＝1，2，…，n）的直觉梯形模糊偏差，则

证明

定理3 设一组取自某直觉梯形模糊总体的样本ξ（ωi），其中ξ（ωi）＝［X（ωi）－l1－l2，X（ωi）－l2，X（ωi），X（ωi）＋l3；μξ（ωi），υξ（ωi）］，ωi∈Θ（i＝1，2，…，n），Θ为参数空间，其样本均值为ξ（ω），则在形如∑（E［ξ（ωi）］－K）2的函数中最小，其中K为任意给定常数。

证明 对于任意给定常数K

定义14 设一组取自某直觉梯形模糊总体的样本ξ（ωi），其中ξ（ωi）＝［X（ωi）－l1－l2，X（ωi）－l2，X（ωi），X（ωi）＋l3；μξ（ωi），υξ（ωi）］，ωi∈Θ（i＝1，2，…，n），Θ为参数空间，且各X（ωi）（i＝1，2，…，n）相互独立，则称

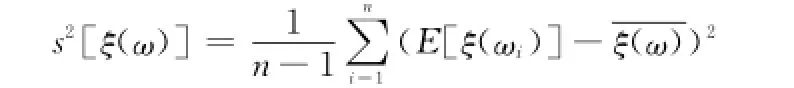
为无偏方差。

定理4 设模糊随机总体ξ具有二阶矩，即E［ξ］＝μ，V［ξ］＝σ2＜＋∞，直觉梯形模糊数ξ（ωi）（i＝1，2，…，n）为一组取自某直觉梯形模糊总体的样本，其中ξ（ωi）＝［X（ωi）－l1－l2，X（ωi）－l2，X（ωi），X（ωi）＋l3；μξ（ωi），υξ（ωi）］，ωi∈Θ（i＝1，2，…，n），Θ为参数空间，其样本均值为样本方差为无偏方差s2［ξ（ω）］，则

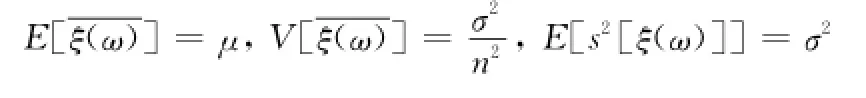
证明 由定义12、定义13可知

注意到

而

因此

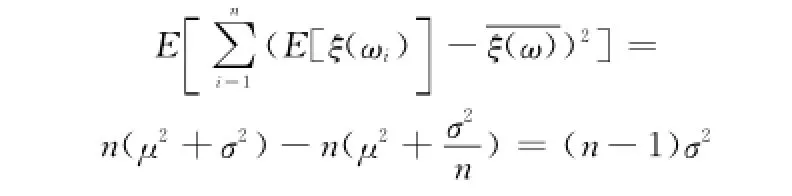
所以

定理5 设直觉梯形模糊数ξ（ωi）（i＝1，2，…，n）为一组取自某指数直觉梯形模糊总体Exp（λ）的样本，E［ξ（ωi）］≥0， λ∈Θ且Θ为参数空间，则λ的最大似然估计为

证明 取自该指数直觉梯形模糊总体的样本的似然函数为

进而可获得其对数似然函数

根据似然函数的含义，需使得上式取得最大值。因此，关于λ求偏导并令其为0，即可得到似然方程如下

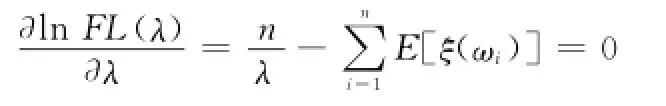
由此可得λ的最大似然估计为

定理6 设直觉梯形模糊数ξ（ωi）（i＝1，2，…，n）为一组取自某正态直觉梯形模糊总体N（μ，σ2）的样本，E［ξ］＝μ，V［ξ］＝σ2，（μ，σ2）∈Θ且Θ为二维参数空间，则μ的最大似然估计为的最大似然估计为

证明 取自该正态直觉梯形模糊总体的样本的似然函数为

进而可获得其对数似然函数

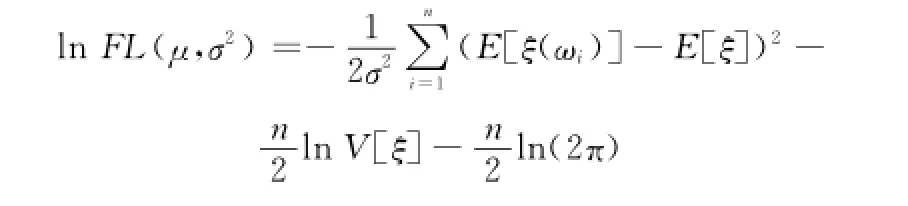
分别关于μ、σ2求偏导并令其为0，即可得到似然方程组如下

因此有μ、σ2的最大似然估计分别为

进而可得

在处理决策者初始输入的样本信息时，定理4～定理6是极为有用的。依据定理4，可通过计算样本均值与方差估计直觉梯形模糊总体的期望与方差，而依据定理5及定理6，可以在假定直觉梯形模糊总体服从指数分布及正态分布的不同情形下，对相应的参数进行统计推断，进而获取总体的分布信息。显然，上述思想为解决具有模糊随机变量的评估信息的合理获取提供了理论依据。

3 基于集对分析理论的直觉梯形模糊随机记分函数

传统记分函数仅适用于直觉模糊数，对于直觉梯形模糊随机变量不具有适用性。事实上，由于直觉梯形模糊随机变量具有随机性，因此对于所有直觉梯形模糊随机样本而言，仅能获取基于直觉梯形模糊数的记分函数序列，而无法确定相应于某一直觉梯形模糊随机变量的记分函数。为此，在获取直觉梯形模糊随机总体的均值与方差之后，依据直觉梯形模糊随机变量的相关性质，将直觉梯形模糊随机变量转化为期望直觉模糊数，并鉴于消除直觉梯形模糊随机变量量纲差异的需要，借鉴随机变量中刻画波动性大小的变异系数概念，定义规范化直觉梯形模糊期望值，在文献［17］的研究基础上，给出基于集对分析理论思想的直觉梯形模糊随机记分函数。

定义15 设ξ为一个直觉梯形模糊随机变量，期望值为E［ξ］，方差为V［ξ］，且其隶属度期望值E［μξ］∈［0，1］、非隶属度期望值为E［υξ］∈［0，1］，则称N［ξ］＝E［ξ］／为其规范化直觉梯形模糊期望值，并规定：当V［ξ］＝0时，N［ξ］＝E［ξ］。

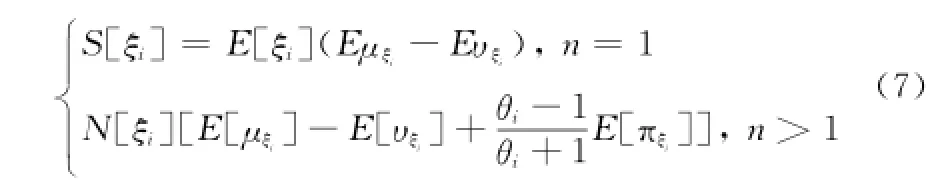
式中

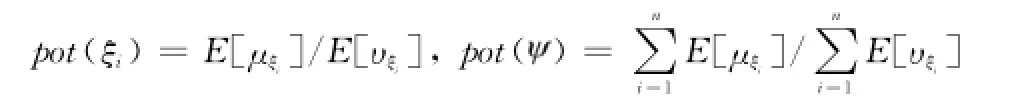
4 基于参数估计与记分函数联合的直觉梯形模糊随机前景决策方法

考虑决策者面临决策问题时存在风险态度及敏感性差异的直觉梯形模糊随机前景决策问题，为便于叙述，首先设下标集合M＝｛1，2，…，m｝，N＝｛1，2，…，n｝，T＝｛1，2，…，t｝。假定有m个备选方案A＝｛A1，A2，…，Am｝，其中Ai为第i个备选方案，i∈M；n个属性C＝｛C1，C2，…，Cn｝，其中Cj为第j个属性，j∈N，各属性之间加性独立；l个决策子周期P＝｛P1，P2，…，Pt｝，其中Pk为第k个属性，k∈T；ω＝（ω1，ω2，…，ωn）代表属性权重向量，其中ωj为第j个属性权重，满足ωj≥0且一般地，效益型及成本型属性较为常见，为规范表述，分别利用NΔ和代表效益型属性和成本型属性的下标集合，满足且假设决策者利用直觉梯形模糊数ξij（ωijk）（i∈M，j∈N，k∈T）表征各决策子周期Pk∈P（k∈T）内针对各备选方案Ai∈A（i∈M）下的属性Cj∈C（j∈N）的评估值，获取直觉梯形模糊时间序列决策矩阵ITr FNijk（k∈T）。在利用直觉梯形模糊样本信息估计总体的未知参数时，对于已知分布类型（本文考虑及两类情形）的直觉梯形模糊总体，不失一般性，分别令CExp和CNorm代表各属性直觉梯形模糊总体服从指数分布及正态分布的属性子集合，其中CExp＝｛C1，C2，…，Cj｝、CNorm＝｛Cj＋1，Cj＋2，…，Cn｝；相应地，利用NExp和NNorm表示属性子集合CExp和CNorm的下标集合，且NExp＝｛1，2，…，j｝、NNorm＝｛j＋1，j＋2，…，n｝，NExp∪NNorm＝N。根据上述资料，对m个备选方案进行排序并择优。

本文将基于参数估计与记分函数联合的前景决策方法解决上述问题，其具体实现步骤如下：

步骤1 在决策周期内，以一定时间间隔为决策子周期，多次获取决策者评估信息样本，构建初始直觉梯形模糊时间序列决策矩

式中，直觉梯形模糊数ξij（ωijk）为取自直觉梯形模糊总体ξij的样本，代表决策者针对第i方案的第j个属性在第k个子周期下的评估值，且i∈M，j∈N，k∈T。

步骤2 首先计算步骤1中直觉梯形模糊时间序列中各直觉梯形模糊数的期望值E［ξij（ωijk）］，进而依据定义12及定义14，分别计算决策者针对各方案各属性的直觉梯形模糊时间序列评估信息的样本均值及样本方差

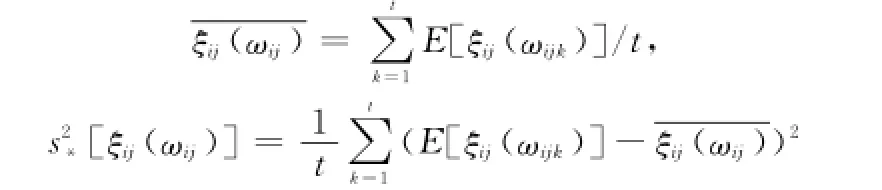
依据定理4及定理5可分别确定相应于各属性评估信息的直觉梯形模糊总体服从指数分布及正态分布情形下的参数估计。对于属性子集合NExp，直觉梯形模糊总体均服从指数分布，则参数λij的极大似然估计为进而可得到ξij～Exp（λij），i∈M，j∈NExp；对于属性子集合NNorm，直觉梯形模糊总体均服从正态分布，则参数μij及的极大似然估计分别为进而可得到同理，设定直觉梯形模糊总体的隶属度及非隶属度均服从正态分布，即μij则参数

通过统计推断获取参数估计值，可进一步构建直觉梯形模糊随机决策矩阵ξ＝［ξij］m×n，其中，对于直觉梯形模糊总体ξij，

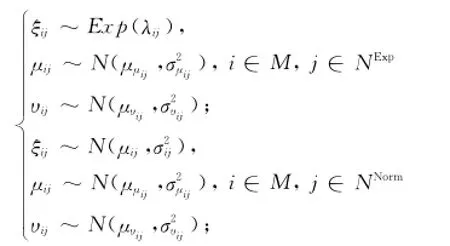
依据定义9及定义10，可将直觉梯形模糊随机决策矩阵转化为带有方差的期望直觉模糊数矩阵，即

为消除属性间量纲差异带来的影响，根据定义15，可进一步将带有方差的期望直觉模糊数矩阵E转化为规范化的期望直觉模糊数矩阵

最后，依据定义16，可计算相应于各直觉模糊数

〈N［ξij］；E［μij］，E［υij］〉ij的记分函数S［ξij］。其中

由此，将规范化的期望直觉模糊数矩阵转化为记分函数矩阵

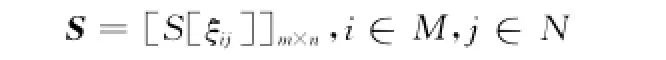
步骤3 目前，针对属性权重的确定方法众多，文献［17］指出灰色系统理论在处理小样本、贫信息方面的优势，故而选用灰色关联方法求解属性权重。其主要思想为：若某个指标信息相对于其他指标而言越匹配于指标体系的平均信息，则说明该指标包含的信息越利于决策，相应的权重也应越大［17，38］。

式中，灰色均值关联度

为灰色关联度矩阵R中的相应于第i个方案下第j个属性的元素。

一般地，取分辨系数χ＝0.5，欧氏距离系数q＝2。由此即可确定属性权重向量ω＝（ω1，ω2，…，ωn）。

步骤4 依据前景理论［39-41］，确定各属性的记分参考点r＝（r1，r2，…，rn），则计算相应于各属性值的面临收益情形下的前景记分价值函数，即前景记分收益价值函数为

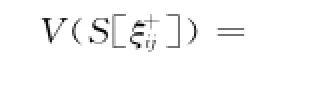
损失情形下的前景记分价值函数，即前景记分损失价值函数为

式中，参数α和β分别为收益和损失区域价值幂函数曲线的凹凸程度，α，β∈［0，1］意味着决策者敏感性呈递减趋势；δ刻画风险厌恶程度，由于决策者对损失敏感性要强于收益，因此需满足δ＞1。依据文献［41- 43］可知，上述参数的确定需要在大量基于决策者心理行为的实验测试结论上给出，不失一般性，本文在具体的案例分析中采用文献［41- 43］所给出的参数取值。

由此，可将记分函数矩阵S＝［S［ξij］］m×n转化为相应的前景价值函数决策矩阵

其中

步骤5 依据步骤3所确定的属性权重向量ω＝（ω1，ω2，…，ωn），可以获取针对各方案的综合前景决策向量

5 案例分析

某机械企业计划采购一批半自动超声波焊接机，目前共有4家该类型产品的供应商（A1，A2，A3，A4）备选，为便于分析，初期主要考虑的4个评价属性分别为：采购总成本（C1）、作业工作效率（C2）、操作便利性（C3）、焊接质量（C4）。其中C1为越小越好的成本型属性，C2、C3、C4为越大越好的效益型属性。决策者在各决策子周期（P1，P2，P3，P4，P5，P6）内以具有不同比例标度的直觉梯形模糊数表征决策信息。并且设定针对各方案下的属性C1、C2的直觉梯形模糊总体服从指数分布，相应地，各方案下的属性C3、C4的直觉梯形模糊总体服从正态分布，而相应的隶属度、非隶属度及犹豫度亦假定服从正态分布。基于本文方法的具体实现步骤如下：

步骤1 获取决策子周期P1、P2、P3、P4、P5和P6内决策者评估信息样本，构建初始直觉梯形模糊时间序列决策矩阵

步骤2 通过统计推断获取参数估计值，可进一步构建直觉梯形模糊随机决策矩阵

其中

依据定义9及定义10，将直觉梯形模糊随机决策矩阵转化为带有方差的期望直觉模糊数矩阵

进而，根据定义15，可进一步将带有方差的期望直觉 模糊数矩阵E 转化为规范化的期望直觉模糊数矩阵

将规范化的期望直觉模糊数矩阵转化为记分函数矩阵

依据式（8）即可确定属性权重向量ω＝（0.260，0.242，0.250，0.248）。

步骤4 依据前景理论，确定各属性的记分参考点r＝（9.081，8.059，11.478，12.032），同时，各参数取值情况分别为α＝0.85，β＝0.92，δ＝2.25［41］。考虑属性C1为成本型属性，而C2，C3，C4为效益型属性，因而可分别计算相应于各属性值的面临收益及损失不同情形下的前景记分价值函数，将记分函数矩阵S转化为相应的前景价值函数决策矩阵

步骤5 依据步骤3所确定的属性权重向量ω＝（0.260，0.242，0.250，0.248），可以获取针对各方案的综合前景决策向量

根据方案的综合前景值，可确定各个方案的排序为

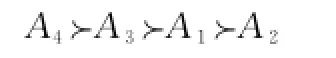
因此，该机械企业应选择备选供应商A4。显然，利用本文所提出的评估值表达方式以及决策方法，该机械企业计划在采购半自动超声波焊接机的过程中可充分将市场调研部门以及采购部门综合以获取更为准确的决策结论。一方面，本文利用直觉梯形模糊随机变量，可以充分反馈决策者评估信息的模糊性与随机性，更为符合实际情形。另一方面，以直觉梯形模糊变量为基础，本文提出了基于直觉梯形模糊样本的参数估计方式，便于后续将其处理为期望、方差等统计特征数，以利于决策方法的实施。此外，基于前景理论而将决策者在应对风险过程中存在的有限理性行为特征纳入考虑，进一步提升了决策方法在实际应用过程中的合理性与有效性。

需要指出的是，针对本文所提出的属性值为直觉梯形模糊随机变量的决策方法的合理性与有效性验证，可将本文方法予以适应性修正以适应直觉梯形模糊多属性群决策，通过对各个决策子周期中所获取的直觉梯形模糊信息单独实施该决策方法，进而将获取相应于各决策子周期的决策结论。作为本文下一阶段的工作，我们将对本文决策方法所获取的决策结论与各不同决策子周期的决策结论予以对比，进而分析决策结论之间的异同及其相关诱因，由此即可验证本文决策方法是合理有效的。

6 结 论

大规模复杂项目通常涉及决策信息的多重不确定性，而本文所定义的直觉梯形模糊随机变量更为细腻地刻画了决策者因学识、经验、能力所限而存在的认知不确定性，对于提升复杂系统决策结论的合理性及准确性具有重要的理论意义及现实价值。由此，文中着重探讨一类具有直觉梯形模糊随机变量的属性权重未知的多属性决策问题，分析并论证了分布类型已知的直觉梯形模糊总体的未知参数估计方法，并通过定义基于集对分析理论思想的模糊随机记分函数判定模糊随机性信息的序关系，进而综合考虑决策者在应对风险过程中存在的有限理性行为特征，提出基于参数估计与记分函数联合的直觉梯形模糊随机前景决策方法。该方法充分结合了模糊数学和概率论与数理统计两个学科的理论思想，将基于模糊数学获取的直觉梯形模糊随机变量的期望值与方差转化为经典统计学中未知参数的极大似然估计，有效规避了基于可信性理论的直觉梯形模糊随机理论体系的不完善所引致的决策结论失真，实现了混合型模糊随机信息的精确化处理，对于处理属性值为混合型、多重型的模糊随机变量的FRMADM问题具有一定参考价值。在后续研究中，将主要考虑直觉梯形模糊总体分布类型未知情形下的非参数估计方法，并重点研究属性权重信息不完全、专家偏好关联的群体直觉梯形模糊随机决策方法。

［1］Bellman R E，Zadeh L A．Decision-making in a fuzzy environment［J］．Management Sciences，1970，17（4）：141- 164．

［2］Liu Y K，Liu B．On minimum-risk problems in fuzzy random decision systems［J］．Computers and Operations Research，2005，32（2）：257- 283．

［3］Nguyen V H．Solving linear programming problems under fuzziness and randomness environment using attainment values［J］．Information Sciences，2007，177（14）：2971- 2984．

［4］Li L Y，Lu Z Z，Song S F．Saddlepoint approximation based line sampling method for uncertainty propagation in fuzzy and random reliability analysis［J］．Scientia Sinica（Technologica），2010，40（10）：1227- 1234．（李璐祎，吕震宙，宋述芳．模糊随机可靠性分析中不确定性传递的鞍点线抽样方法［J］．中国科学（技术科学），2010，40（10）：1227- 1234．）

［5］Sakawa M，Matsui T．Interactive fuzzy random cooperative twolevel linear programming through level sets based probability maximization［J］．Ex pert Systems with Applications，2013，40（4）：1400- 1406．

［6］Andrés-Sáncheza J，Puchades L G-V．Using fuzzy random variables in life annuities pricing［J］．Fuzzy Sets and Systems，2012，188（1）：27- 44．

［7］Xiao X Y．Failure probability analysis of sensitive equipment due to voltage sags using fuzzy-random assessment method［J］．IEEE Trans.on Power Delivery，2010，25（4）：2970- 2975．

［8］Xu J P，Liu Y G．Multi-objective decision making model under fuzzy random environment and its application to inventory problems［J］．Information Sciences，2008，178（14）：2899- 2914．

［9］Liu Y K．The approximation method for two-stage fuzzy random programming with recourse［J］．IEEE Trans.on Fuzzy Systems，2007，15（6）：1197- 1208．

［10］Liu Y K，Liu B．Fuzzy random variables：a scalar expected value operator［J］．Fuzzy Optimization and Decision Making，2003，2（2）：143- 160．

［11］Liu Y K，Liu B．A class of fuzzy random optimization：expected value models［J］．Information Sciences，2003，115（1／2）：89- 102．

［12］Wang M．Fuzzy random multi-attribute decision making method［C］∥Proc.of the 5th IEEE International Conference on Fuzzy Systems and Knowledge Discovery，2008．

［13］Zhang Y Q，Zhao R Q，Ning Y F．A SPSA algorithm for solving fuzzy random expected value models［C］∥Proc.of the 14th IEEE International Conference on Fuzzy Systems，2005．

［14］Zarghami M，Szidarovszky F，Ardakanian R．A fuzzy-stochastic OWA model for robust multi-criteria decision making［J］．Fuzzy Optimization and Decision Making，2008，7（1）：1- 15．

［15］Wang J Q，Gong L．Interval probability fuzzy random multicriteria decision-making approach based on expectation-hybrid entropy［J］．Control and Decision，2009，24（7）：1065- 1069．（王坚强，龚岚．基于期望值 混合熵的区间概率模糊随机多准则决策方法［J］．控制与决策，2009，24（7）：1065- 1069．）

［16］Wang J Q，Li J J．Intuitionistic random multi-criteria decisionmaking approach based on score functions［J］．Control and Decision，2010，25（9）：1297- 1306．（王坚强，李婧婧．基于记分函数的直觉随机多准则决策方法［J］．控制与决策，2010，25（9）：1297- 1306．）

［17］Li P，Liu S F，Zhu J J．Intuitionistic fuzzy stochastic multi-criteria decision-making methods based on prospect theory［J］．Control and Decision，2012，27（11）：1601- 1606．（李鹏，刘思峰，朱建军．基于前景理论的随机直觉模糊决策方法［J］．控制与决策，2012，27（11）：1601- 1606．）

［18］Colubi A，Corral N，Gonzailez-Rodriguez G，et al．A determination coefficient for fuzzy random variables in a fuzzy arithmetic-based linear model［C］∥Proc.of the IEEE International Conference on Fuzzy Systems，2007．

［19］Dey O，Chakraborty D．A fuzzy random continuous review inventory system［J］．International Journal of Production Economics，2011，132（1）：101- 106．

［20］KoçM L，Balasb C E．Reliability analysis of a rubble mound breakwater using the theory of fuzzy random variables［J］．Applied Ocean Research，2013，39（1）：83- 88．

［21］Liu Y，Tang W S，Zhao R Q．Reliability and mean time to failure of unrepairable systems with fuzzy random lifetimes［J］．IEEE Trans.on Fuzzy Systems，2007，15（5）：1009- 1026．

［22］Zhang Z，Xu J P．A mean-semivariance model for stock portfolio selection in fuzzy random environment［C］∥Proc.of the IEEE International Conference on Industrial Engineering and Engineering Management，2008．

［23］Zhao R Q，Tang W S，Yun H L．Random fuzzy renewal process［J］．European Journal of Operational Research，2006，169（1）：189- 201．

［24］Zhao R Q．Some properties of fuzzy random renewal processes［J］．IEEE Trans.on Fuzzy Systems，2006，14（2）：173- 179．

［25］González-Rodrígueza G，Blancobá，Colubib A．Estimation of a simple linear regression model for fuzzy random variables［J］．Fuzzy Sets and Systems，2009，160（3）：357- 370．

［26］Atanassov K．Intuitionistic fuzzy sets［J］．Fuzzy Sets and Systems，1986，20（1）：87- 96．

［27］Wang J Q．Overview on fuzzy multi-criteria decision-making approach［J］．Control and Decision，2008，23（6）：601- 607．（王坚强．模糊多准则决策方法研究综述［J］．控制与决策，2008，23（6）：601- 607．）

［28］Wan S P．Survey on intuitionistic fuzzy multi-attribute decision making approach［J］．Control and Decision，2010，25（11）：1601- 1606．（万树平．直觉模糊多属性决策方法综述［J］．控制与决策，2010，25（11）：1601- 1606．）

［29］Wang J Q，Nie R R．Multi-criteria group decision-making method based on intuitionistic trapezoidal fuzzy information［J］．Systems Engineering-Theory&Practice，2012，32（8）：1747-1753．（王坚强，聂荣荣．基于直觉梯形模糊信息的多准则群决策方法［J］．系统工程理论与实践，2012，32（8）：1747 -1753．）

［30］Chen Z S，Li Y L．An approach for group multi-attribute decision making based upon prospect intuitionistic trapezoidal fuzzy number Choquet integral operator［J］．Control and Decision，2014，29（6）：1053- 1063．（陈振颂，李延来．基于前景ITFNCI算子的群体MULTIMOORA决策方法［J］．控制与决策，2014，29（6）：1053- 1063．）

［31］Liu B，Liu Y-K．Expected value of fuzzy variable and fuzzy expected value models［J］．IEEE Trans.on Fuzzy Systems，2002，10（4）：445- 450．

［32］Zadeh L A．Fuzy sets as a basis for a theory of possibility［J］．Fuzzy Sets and Systems，1978，1（1）：3- 28．

［33］Liu B D，Peng J．A course in uncertainty theory［M］．Beijing：Tsinghua University Press，2005．（刘宝碇，彭锦．不确定理论教程［M］．北京：清华大学出版社，2005．）

［34］Hao F F，Liu Y K，Wang S．The variance formulas for triangular fuzzy random variables［C］∥Proc.of the 7th International Conference on Machine Learning and Cybernetics，2008．

［35］Wang S M，Liu Y K，Watada J．Fuzzy random renewal process with queuing applications［J］．Computers&Mathematics with Applications，2009，57（7）：1232- 1248．

［36］Yang L X，Ji X Y．Some properties of expected value operators of fuzzy variables and fuzzy random variables［C］∥Proc.of the 6th International Conference on Fuzzy Systems and Knowledge Discovery，2009．

［37］Chen X R．Probability and statistics［M］．Beijing：Science Press，2000．（陈希孺．概率论与数理统计［M］．北京：科学出版社，2000．）

［38］Liu S F，Dang Y G，Fang Z G．Theory and application of grey system［M］．Beijing：Science Press，2004．（刘思峰，党耀国，方志耕．灰色系统理论及其应用［M］．北京：科学出版社，2004．）

［39］Kahneman D，Tversky A．Prospect theory：an analysis of decision under risk［J］．Econometrica，1979，47（2）：263- 292．

［40］Tversky A，Kahneman D．Advances in prospect theory：cumulative representation of uncertainty［J］．Journal of Risk and Uncertainty，1992，5（4）：297- 323．

［41］Bleichrodt H，Schmidt U，Zank H．Additive utility in prospect theory［J］．Management Science，2009，55（5）：863- 873．

［42］Fan Z P，Liu Y，Shen R J．Risk decision analysis method for emergency response based on prospect theory［J］．Systems Engineering-Theory&Practice，2012，32（5）：977- 984．（樊治平，刘洋，沈荣鉴．基于前景理论的突发事件应急响应的风险决策方法［J］．系统工程理论与实践，2012，32（5）：977- 984．）

［43］Zhang X，Fan Z P．Method for risky hybrid multiple attribute decision making based on prospect theory［J］．Journal of Systems Engineering，2012，27（6）：772- 781．（张晓，樊治平．基于前景理论的风险型混合多属性决策方法［J］．系统工程学报，2012，27（6）：772- 781．）

Approach for intuitionistic trapezoidal fuzzy random prospect decision making based on the combination of parameter estimation and score functions

CHEN Zhen-song1，2，XIONG Sheng-hua1，2，LI Yan-lai1，2，QIAN Gui-sheng3
（1.School of Transportation and Logistics，Southwest Jiaotong University，Chengdu 610031，China；2.Nation and Region Combined Engineering Lab of Intelligentizing Integrated Transportation，Southwest Jiaotong University，Chengdu 610031，China；3.Department of Systems Engineering and Engineering Management，City University of Hong Kong，999077，Hong Kong）

The operational laws of the intuitionistic trapezoidal fuzzy number are improved，a concept of instuitionistic trapezoidal fuzzy random variable（ITr FRV）is introduced based on the intuitionistic trapezoidal fuzzy number and the trapezoidal fuzzy random variable，and the related properties of an ITrFRV are also proposed and proved．With respect to a problem of multiple attribute decision making（MADM），in which attribute weights are unknown and attribute values are given in terms of intuitionistic trapezoidal fuzzy random variables，considering the decision-maker’s psychological behavior，an approach for intuitionistic trapezoidal fuzzy random prospect decision making is proposed based on the combination of parameter estimation and score functions．Firstly，by acquiring intuitionistic trapezoidal fuzzy sample information in different periods of the decision making process，the unknown parameters of entire intuitionistic trapezoidal fuzzy populations with a known distribution pattern are estimated，and an intuitionistic trapezoidal fuzzy random matrix is obtained．Secondly，an expectation-variance intuitionistic fuzzy number matrix is constructed，and then the concept of a fuzzy random ___score function is defined to transform a normalized expectation intuitionistic fuzzy number matrix into a scorefunction matrix．Finally，the prospect theory is utilized to calculate a prospect score function，attribute weights are determined by constructing a grey system theory model，and then a ranking of alternatives are obtained according to comprehensive prospect score values．A practical example is introduced to show the feasibility and effectiveness of the proposed approach．

multi-attribute decision making；intuitionistic trapezoidal fuzzy random variable（ITr FRV）；parameter estimation；score function；prospect theory

C 934

A

10．3969／j．issn．1001-506X．2015．04．20

陈振颂（1988-），男，博士研究生，主要研究方向为决策理论与方法、系统建模与优化。E-mail：czs7328026＠126．com

熊升华（1988-），男，博士研究生，主要研究方向为智能控制与应用、系统建模与优化。E-mail：xsh1841＠163．com

李延来（1971 ），通信作者，男，教授，博士，主要研究方向为决策理论与方法、系统建模与优化。E-mail：lyl_2001＠163．com

钱桂生（1958-），男，副教授，博士，主要研究方向为质量体系与管理、新产品设计与开发、决策支持系统。E-mail：mekschin＠cityu．edu．hk

1001-506X（2015）04-0851-12

2014- 03- 07；

2014- 09- 10；网络优先出版日期：2014- 09- 28。

网络优先出版地址：http：∥w ww．cnki．net／kcms／detail／11．2422．TN．20140928．1719．020．html

国家自然科学基金（71371156，70971017）；西南交通大学优秀博士学位论文培育项目资助课题