基于先验信息的多假设模型中断航迹关联算法

齐 林，王海鹏，熊 伟，董 凯

（1．海军航空工程学院信息融合研究所，山东烟台264001；2．飞行器测控与通信教育部重点实验室，重庆400044）

基于先验信息的多假设模型中断航迹关联算法

齐 林1，2，王海鹏1，2，熊 伟1，董 凯1

（1．海军航空工程学院信息融合研究所，山东烟台264001；2．飞行器测控与通信教育部重点实验室，重庆400044）

针对经典的中断航迹关联算法在机动目标环境下航迹预测准确性差、关联效果恶化严重的问题，提出基于先验信息的多假设运动模型中断航迹关联算法。所提算法充分利用目标属性、目标运动特征、使用场景等先验信息，基于多假设思想，建立多种可能的目标运动模型并实施航迹预测，基于位置和速度信息的模糊相关函数描述预测航迹与新起始航迹的模糊匹配关系，最后基于多项式拟合原理连接满足关联关系的新、老航迹。经仿真验证，在中断区间目标发生机动运动的条件下，所提算法的关联效果相对于经典的中断航迹关联算法有显著提升。所提算法对于复杂环境具有较强的适应能力，经50次蒙特卡罗仿真，在中断时间小于18个滤波周期条件下，机动目标的平均正确关联率达到90%以上，机动环境的全局关联正确率达到85%以上。

中断航迹关联；先验信息；多假设；模糊相关函数；航迹拟合

0 引 言

由于目标机动、多普勒雷达照射盲区、长采样间隔和低探测率等原因，雷达对目标的跟踪常常发生航迹中断。航迹中断对信息融合会造成严重的干扰，因而中断航迹的配对关联是雷达数据处理领域亟需解决的关键问题之一。中断航迹的配对关联及连接问题早在20世纪80年代就被提出［1］，最近几年已成为国内外学者的关注热点。文献［2］提出了基于统计加权的中断航迹关联（track segment association，TSA）算法，为后续TSA方法的研究发展奠定了基础。该算法利用交互多模型［3-5］实施目标跟踪，将新航迹逆向预测至老航迹最后一个状态更新点，由新、老航迹对该点作状态估计的统计距离判断是否满足关联条件，并用二维分配方法处理多义性问题；文献［6- 7］基于上述方法及其改进算法解决了因目标停走机动造成的地面目标TSA问题；文献［8］将上述方法应用于解决弹道目标的TSA。TSA及其改进算法对于运动状态相对稳定的TSA问题具有很好的关联效果，但当中断区间目标发生机动运动时，基于中断前后的量测信息预测中断区间目标运动状态的准确性很差，造成中断航迹关联失准，另一方面，长时间航迹中断造成的误差积累加重了预测航迹与真实航迹的偏差，TSA效果恶化严重。文献［9］提出的多普勒盲区条件下的多假设运动模型目标跟踪方法为TSA问题的研究提供了新思路。该算法基于多普勒盲区条件下目标在中断区间多种可能的角速度取值预测目标航迹，对于中断区间目标可能发生的小幅机动具有一定的适应性。但该算法仅适用于多普勒盲区条件下弱机动单目标航迹中断，应用范围比较局限。

针对现有算法的上述缺陷，为解决多机动［10］目标中断航迹关联问题，本文提出基于先验信息的多假设运动模型TSA算法。该算法充分考虑目标属性、目标运动特征、使用场景等先验信息实施航迹段粗关联判断，对于满足粗关联关系的新、老航迹，基于多假设思想设置多种可能的目标运动模型并进行航迹预测，基于目标运动特征的模糊相关函数［11-15］描述多条预测航迹与新起始航迹的模糊匹配关系，选出其中最大的模糊相似度作为新、老航迹的匹配关系，并使用二维分配原理确定目标间的关联关系，最后使用多项式拟合［1617］方法连接满足关联关系的新、老航迹。

1 中断航迹预处理及粗关联

1.1 目标运动状态提取

雷达自动跟踪战场环境中的多个运动目标，生成环境中的目标运动态势。目标机动等原因造成的航迹中断使环境中形成多条零散的航迹段，提取每条航迹段的第一个和最后一个状态更新点，对满足时间先后顺序的多对新、老航迹段实施配对关联。某对新、老航迹表示为

老航迹

新航迹

1.2 基于先验信息的中断航迹粗关联

在战场环境或其他具体应用背景下，目标的部分属性信息可以先验获得，如飞行器飞行速度区间、加速度区间、转弯角速度范围等；基于目标飞行高度，飞行负载等附加信息可进一步限定上述运动特征的范围，作为中断航迹粗关联的先验条件。基于先验信息的中断航迹目标运动特征匹配可简单有效地排除大部分无关联可能的中断航迹段，简化航迹匹配关联的运算量。

本文基于目标运动特征信息设置粗关联判断。

（1）速度匹配：目标在中断区间位移与时间的比值满足目标速度门限，即

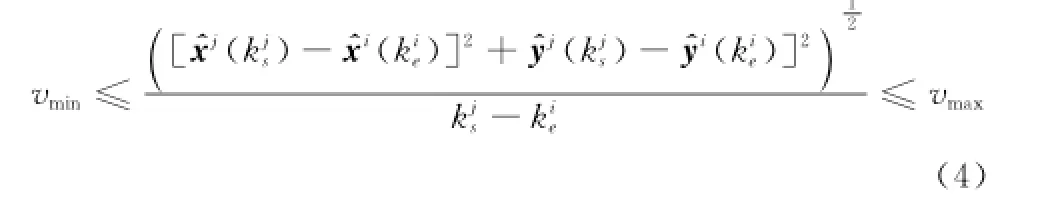
（2）加速度匹配：目标在中断区间的速度变化率小于目标加速度门限，即

（3）角速度匹配：目标在单位时间的转弯角度小于目标角速度门限，即

式中

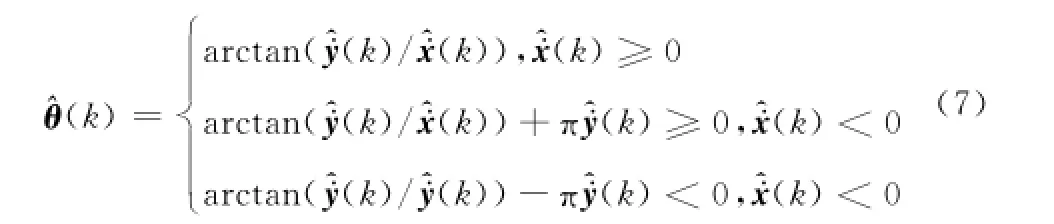
2 基于多假设运动模型的TSA

2.1 基于多假设运动模型的航迹预测

目标在中断区间的运动状态未知，但目标的基本运动形式包括匀速运动、匀加速运动和匀速转弯运动，其他复杂的运动形式大多由上述3种基本运动形式时空叠加组合而成。为描述中断区间目标的运动状态，本文假定目标在每个滤波周期内做各坐标轴加速度恒定的匀加速运动或角速度恒定的匀速转弯运动（匀速直线运动可看作上述两种运动形式的特例），并基于上述假设的多种可能的运动参数预测目标的运动状态。

根据先验信息推算出目标加速度取值范围为［0，amax］，将最大加速度amax进行Na－1等分，得到每个坐标轴上Na种可能的加速度取值，则空间nx维加速度取值的总模型数为基于老航迹最后一个状态更新点进行中断区间航迹多假设预测，利用种加速度模型递推得到下一时刻目标的种状态预测，假设第n种运动模型横、纵坐标加速度取值分别为，将其赋值给时刻老航迹运动状态矢量

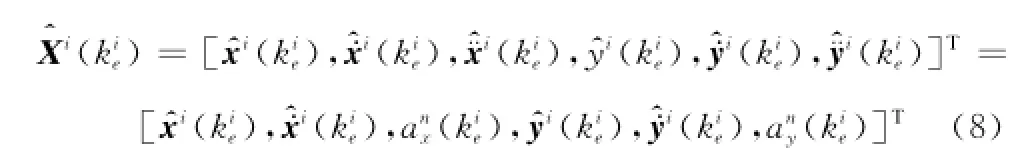
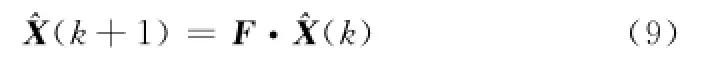
式中

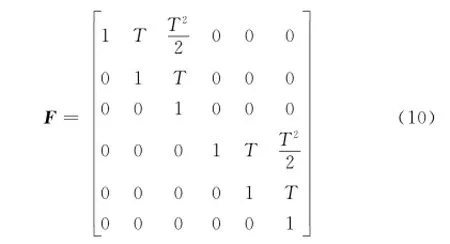
同理推算出目标匀速转弯运动的角速度取值范围为［0，ωmax］，将最大角速度ωmax进行Nω－1等分，得到Nω种可能的角速度取值，假设第n种匀速转弯模型角速度取值为ωn，其中）时，ωn取正值，时，ωn取负值，状态转移矩阵［18］为

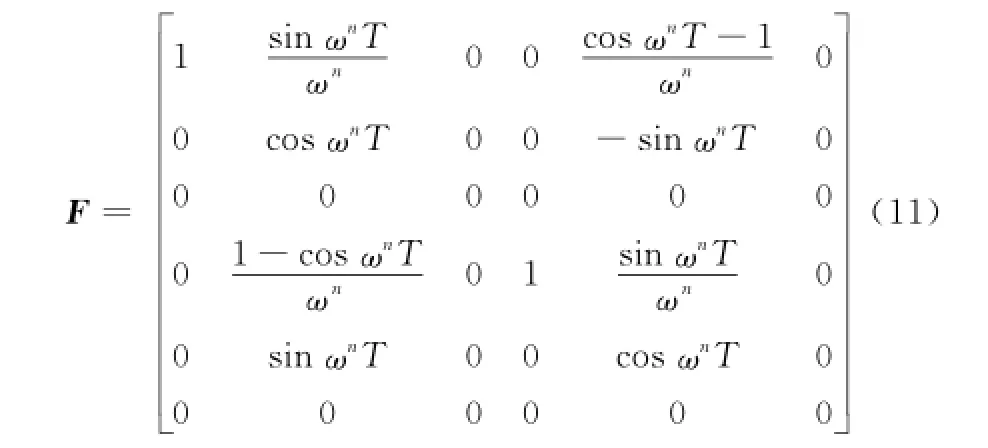
2.2 基于目标运动特征的航迹模糊相似度

针对单目标TSA问题，当新航迹起始时刻状态估计矢量

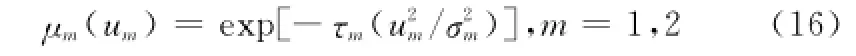
式中，um是第m个模糊因素；σm是第m个模糊因素的展度；τm是调整度。

u1是位置模糊因素；u2是速度模糊因素。老航迹Ti和新航迹Tj基于多假设运动模型的模糊相似度表示为

2.3 中断航迹拟合

本文使用多项式拟合方法连接满足关联关系的中断航迹，拟合数据使用老航迹最后L个状态更新点的位置矢量

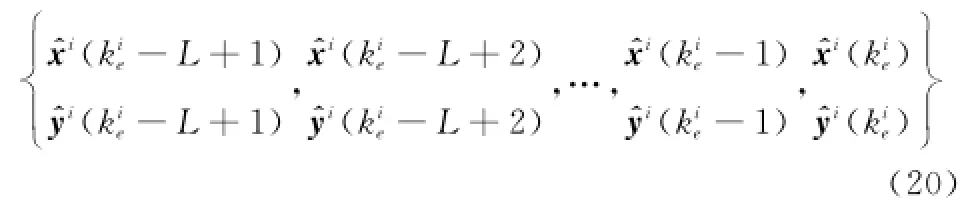
和新航迹起始的L个状态更新点的位置矢量

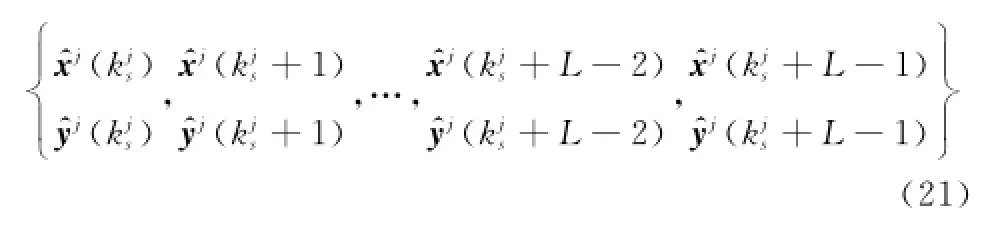
假设目标在X轴上进行匀速运动，则X轴上目标位置和时间近似满足线性关系；目标进行匀加速运动时，位置和时间的关系近似满足二维曲线；目标进行匀速转弯运动时，位置和时间近似满足更高维的曲线关系。由于中断区间目标运动状态未知，考虑随机误差对目标位置的影响，凭借经验使用4阶多项式拟合各坐标轴上中断的航迹数据，将老航迹和新航迹连接起来。

综上所述，基于先验信息的多假设运动模型TSA算法流程如图1所示。

图1 算法流程图

3 仿真验证

3.1 单目标TSA流程仿真

空域中有某飞行器进行等高巡逻飞行，起始位置（0，7 000 m），起始速度（0，－150 m／s）。0～400 s时间段，目标以起始速度进行匀速飞行；400～500 s，目标进行各坐标轴加速度恒定的匀加速曲线飞行，加速度取值（1．5 m／s2，1．5 m／s2）；500 s后，目标恢复匀速飞行。雷达采样间隔T＝5 s，跟踪时间700 s，400～500 s时间段内目标量测数据丢失造成目标航迹中断。忽略系统误差的影响，雷达量测引入均值为0、距离标准差80 m、方位角标准差存在0．3°的随机误差，采用匀速直线运动卡尔曼滤波算法实施目标跟踪，目标真实轨迹、雷达量测点迹、滤波点迹如图2和图3所示。由于航迹起始阶段滤波精度较差，本文对新航迹实施T为负值的逆向滤波，提取新航迹起始时刻目标运动状态。

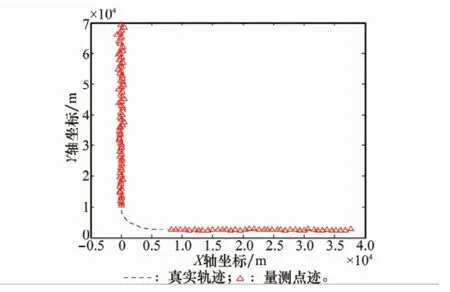
图2 目标真实轨迹与观测点迹

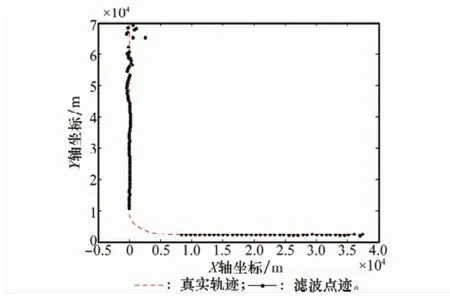
图3 目标真实轨迹与滤波点迹

由先验信息限定目标速度取值范围［100 m／s，500 m／s］，目标加速度取值范围［0，5 m／s2］，飞行器平飞（无侧滑）转弯的最大角速度3（°）／s，经验证，中断前后的新、老航迹满足粗关联条件。基于多假设运动模型的航迹预测，单轴匀加速多假设模型个数取值Na＝11，匀速转弯多假设模型个数Nω＝31，按图1所示流程对老航迹进行中断区间目标运动状态预测至新航迹起始时刻，预测航迹如图4和图5所示。基于模糊相关函数求出预测状态与新航迹起始状态的模糊相似度，τ1＝τ2＝0.001，a1＝a2＝0.5，求得的匀加速多假设模型下新航迹起始时刻估计状态与老航迹预测状态最大相似度为0.633 7，匀速转弯多假设模型下最大相似度为0.373 4。基于不同阶数的多项式拟合中断区间目标航迹，老、新航迹拟合数据长度L＝5，各阶拟合航迹如图6所示，拟合航迹与真实航迹的均方误差如图7所示，图中N表示拟合阶数，如图7所示4阶、5阶拟合航迹与目标真实航迹均方偏差最小，拟合匹配性最好。N＜4时，因多项式阶数较低，拟合曲线难以准确描述航迹走势；N＞5时，拟合曲线波动较大，与目标实际运动状态不符。

图4 匀加速模型目标预测状态

图5 匀速转弯模型目标预测状态

3.2 多机动目标环境下算法性能比较

为验证本文算法相对于经典的TSA算法的优越性能，特别是目标在中断区间发生机动运动条件下的关联效果，设置如图8所示的飞行目标仿真环境。环境中的目标个数为5，中断前后目标均保持匀速直线飞行状态，中断区间目标可能转变为匀加速曲线飞行或匀速转弯飞行等机动运动，雷达量测更新周期T＝5 s，中断时间为T的整数倍K，定义K为中断间隔。各目标运动状态如下：目标1起始位置（－27 000 m，0），起始速度（250 m／s，0），中断区间仍保持匀速直线飞行；目标2起始位置（－30 000 m，1 000 m），起始速度（300 m／s，0），中断区间转变成匀加速飞行状态，加速度（－0．5 m／s2，－1．7 m／s2），目标3起始位置（－25 000 m，－1 000 m），起始速度（200 m／s，0），中断区间转变成加速度（－0．8 m／s2，1．4 m／s2）的匀加速飞行状态；目标4起始位置（－30 000 m，－2 000 m），起始速度（300 m／s，0），中断区间匀速转弯飞行，角速度ω＝π／200（rad／s）；目标5起始位置（－27 500 m，2 000 m），起始速度（250 m／s，0），中断区间匀速转弯飞行，角速度ω＝－π／150（rad／s）。雷达量测引入测距标准差80 m，测方位角标准差存在0．3°的高斯随机误差。

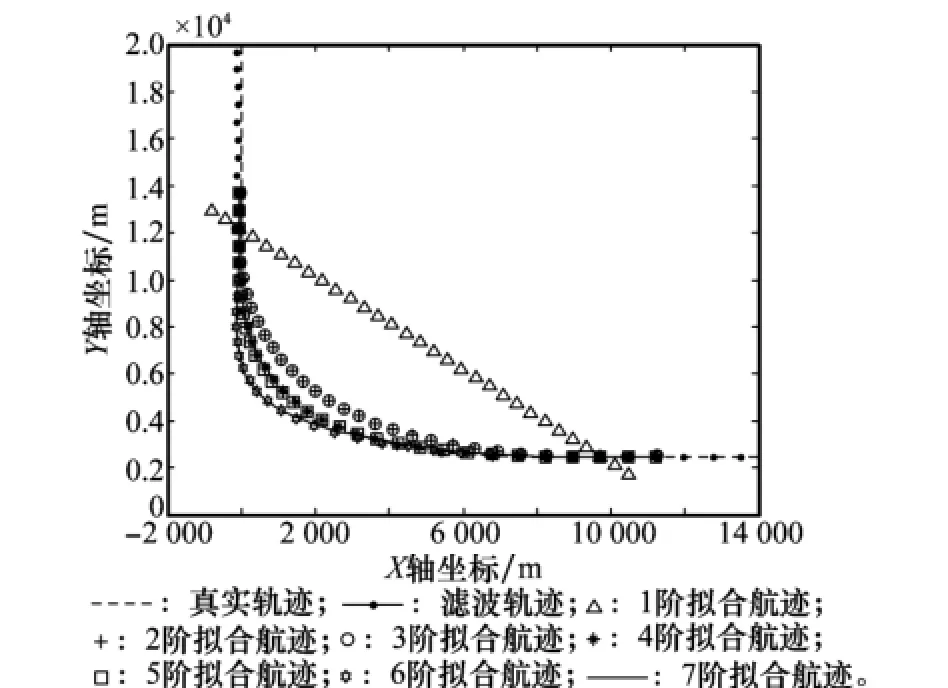
图6 各阶拟合航迹

图7 各阶拟合航迹的均方误差

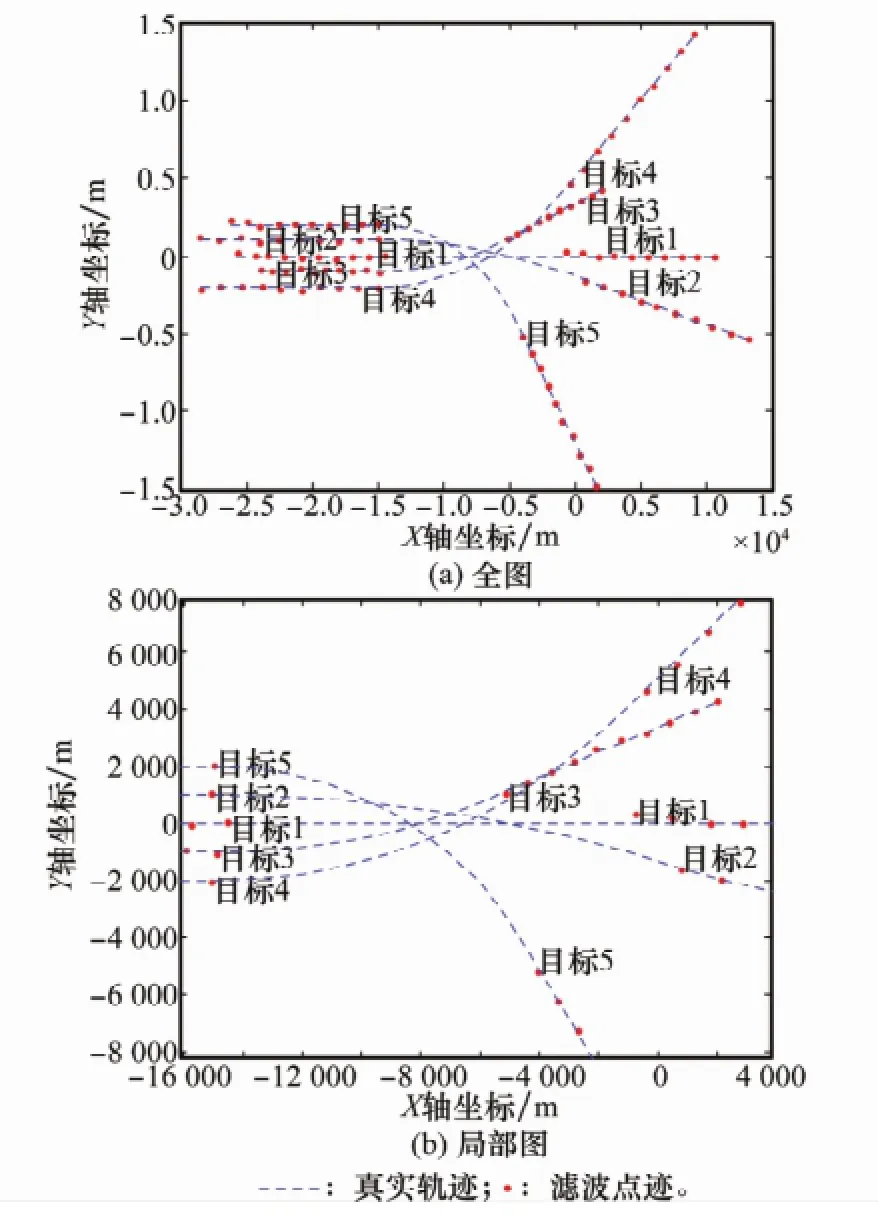
图8 多目标环境真实轨迹与滤波点迹

为描述算法的关联效果，这里需要定义TSA的几个评价指标。全局关联正确率为

式中，M表示实验的蒙特卡罗仿真次数；m表示实验中全局关联正确次数。全局关联正确指一次蒙特卡罗仿真实验中每条老航迹唯一地与和它对应的新航迹配对关联，每条新航迹唯一地与和它对应的老航迹配对关联。平均正确关联率为

平均错误关联率为

平均漏关联率为

式中，n表示一次实验中发生航迹中断的目标个数；nt表示正确关联的目标个数；nf表示错误关联的目标个数；nn表示漏关联的目标个数；nt＋nf＋nn＝n。故Rta表示正确关联率，即一次实验中正确关联的目标个数与目标总数的比值，同理Rfa表示错误关联率，Rna表示漏关联率。本实验结果由50次蒙特卡罗仿真求均值得到，Rta、Rfa、Rna分别表示关联结果中的目标平均正确关联率、平均错误关联率、平均漏关联率。

设置不同的中断间隔长度K，基于50次蒙特卡罗仿真，分别使用经典的TSA算法和本文算法关联环境中的中断航迹。TSA算法的详细计算流程参考文献［2］，本文使用交互多模型算法跟踪运动目标，将新航迹逆向预测至老航迹最后一个状态更新点，基于TSA算法实施关联判断。基于多假设运动模型的航迹预测及模糊相关函数的求法同3.1节，单轴匀加速多假设模型个数Na＝21，匀速转弯多假设模型个数Nω＝31，匀加速模型隶属度函数中，τ1＝τ2＝1，匀速转弯模型隶属度函数中，τ1＝τ2＝0.2，权值a1＝a2＝0.5，判断可能关联的最小隶属度取值0.6。随着中断间隔长度K的增长，各目标关联正确次数如表1所示，各关联评价参数如表2所示。如表1所示，TSA算法的环境适应能力较差。当目标维持在匀速直线运动或加速度取值较小的匀加速运动条件下（表1中TSA算法目标1和目标3），且要求中断间隔K不大于10时，TSA算法具有较高的关联正确次数；当目标加速度增大或进行匀速转弯运动时，由于中断区间航迹曲率较大，基于非中断区间的量测数据预测中断区间目标运动状态的准确性较低，TSA算法难以准确实施航迹关联判断；当中断间隔大于10时，由于误差积累造成航迹预测准确性骤降，同样造成航迹关联判断失准。如表2所示，当中断间隔大于10时，TSA算法目标平均正确关联率降至20%以下，平均错误关联率和平均漏关联率剧增，TSA算法在这种复杂环境下已不具备使用价值。

表1 算法关联正确次数

表2 算法关联评价参数 %

本文算法对于中断区间目标发生机动运动具有较强的适应能力。在表1中所列的不同目标机动程度、不同中断间隔条件下，本文算法均具有较高的关联正确次数。比较表2中相同仿真条件下不同算法所得实验结果可知，本文算法具有明显更高的全局关联正确率和目标平均正确关联率，平均错误关联率和平均漏关联率更低，说明本文算法对于TSA算法的关联效果具有显著提升。考虑两种算法的关联判断原理，TSA算法基于中断前后的目标量测估计中断区间的目标运动状态并实施统计距离判断，当中断区间目标未发生机动运动且估计误差较小时，这种算法具有一定的可用性，当中断区间目标发生机动运动或中断时间较长、预测误差积累较大时，航迹预测准确性无法保证，算法关联效果不可信。本文使用基于多假设运动模型的航迹预测，考虑中断区间目标可能发生的机动运动，基于多种可能的运动模型和参数分别预测航迹走势，并基于模糊相关函数选择可能性最大的运动模型匹配新、老航迹。当中断间隔逐渐增大至18以上时，各目标关联正确次数、全局关联正确率、目标平均正确关联率均有所下降，考虑到中断间隔逐渐增大导致误差逐渐积累，造成预测偏差逐渐增大，上述关联性能的下降在合理的范围内。

从原理上分析，当航迹预测偏差较小时，基于多假设运动模型的TSA算法的关联性能依赖于模型库中的模型个数，当模型个数多到确保有一种假设运动模型可以精确描述目标的真实运动状态，预测航迹与新起始航迹的高匹配度将确保航迹的准确关联。当模型个数较少，多假设的运动模型均与目标实际运动模型差距较大，预测航迹与新起始航迹间匹配程度较低，关联失败。表3是中断间隔K＝10，不同模型个数条件下基于多假设运动模型的TSA算法的关联评价参数，实验结果在一定程度上验证了上文的论述，在模型个数未达到足够描述目标运动状态的前提下，算法的关联性能随模型个数增多而增强。在算法具体应用时，模型个数和参数的选取应综合考虑目标属性、应用背景、过往经验等先验信息。模型个数选取过少将导致关联效果较差；模型个数选取过多对提高关联效果无实质帮助，还会增加计算复杂度，降低算法的实时性。

表3 模型个数不同条件下本文算法关联评价参数 %

实际情况下目标的机动运动形式不限于匀加速和匀速转弯模型，且中断区间内目标运动形式也可能发生不止一次的转变，但大多复杂的运动形式可由简单的运动模型时空叠加组合而成。本文算法对于解决机动目标的TSA问题具有重要的参考价值，随着经验的不断积累，研究的继续深入，模型库中可加入更多的运动模型，使多假设的航迹预测更贴近目标的真实运动状态，本文算法的关联效果进一步提升。

4 结 论

为解决中断区间目标发生机动运动的TSA问题，本文提出了基于先验信息的多假设运动模型TSA算法，经仿真验证，得到针对该算法的如下结论：

（1）基于异构信息的多源融合可利用目标属性、目标运动特征、环境条件等先验信息提高目标关联、识别的准确性。本文提出的基于先验信息的多假设运动模型中断航迹配对关联算法充分考虑目标中断区间可能发生的机动运动形式，建立多种可能的目标运动模型实施航迹预测和关联，并基于模糊相关函数和二维分配原理选择匹配最好的新、老航迹，相比经典的TSA算法，大幅提高了多机动目标环境下全局关联正确率和目标平均正确关联率。

（2）本文基于目标属性、目标运动特征、环境条件等信息设定TSA的先验条件，用于粗关联和精细关联中多假设运动模型参数的选取。具体应用时，基于雷达回波特征信息可实施航迹的目标属性识别，获取目标运动特征；基于使用环境的先验信息也可进一步限定目标航行条件。上述信息的收集选取过程中可能存在证据一致、互补、冲突等情况，需要基于证据理论综合提取最优信息，本文不进行这方面内容的具体研究，只研究先验信息选定情况下的中断航迹配对关联算法。

（3）基于先验信息的多假设运动模型TSA算法对于航迹的长中断间隔具有较强的适应能力，但当中断间隔K≥18时，随着K继续增大，关联效果明显下降。考虑长时间的量测丢失导致航迹预测误差逐渐积累，航迹预测准确性降低，上述问题的出现在合理的范围。

（4）为限制目标运动模型的个数，本文进行整个中断区间目标运动形式恒定的假设，实际情况下，由于中断时间较短（中断时间过长时航迹配对关联已失去意义），上述假设具有比较普遍的意义。对于中断区间目标机动运动模型变化的情况，仅仅基于位置层信息的TSA将十分困难。可考虑基于雷达回波中目标属性信息的识别融合研究上述问题，当使用条件中不存在上述信息时，可尝试基于时间维度的多假设航迹预测。

（5）基于先验信息的多假设运动模型TSA算法的关联性能在一定程度上随模型个数的增多而增强。在实际使用中，模型个数和参数范围的选择应充分考虑目标属性、目标运动特征、环境条件等先验信息，模型个数选取过少导致航迹预测准确性差，模型个数选取过多对提高关联效果无实际意义，还会降低算法的实时性。

［1］Mucci R，Arnold J，Bar-Shalom Y．Track segment association with a distributed field of sensors［J］．Acoustical Society of America，1985，78（4）：1317- 1324．

［2］Yeom S W，Kirubarajan T，Bar-Shalom Y．Track segment association，fine-step IMM and initialization with Doppler for improved track performance［J］．IEEE Trans.on Aerospace and Electronic Systems，2004，40（1）：293- 309．

［3］Wang X，Han C Z．An improved multiple model GM-PHD filter for maneuvering target tracking［J］．Chinese Journal of Aeronautics，2013，26（1）：179- 185.

［4］Li X L．Improved joint probabilistic data association method based on interacting multiple model［J］．Journal of Networks，2014，9（6）：1572- 1597．

［5］Fu X Y，Jia Y M，Liu X H．Optimal set integer programming algorithm for multiple maneuvering targets tracking in clutter［J］．Journal of Systems Engineering and Electronics，2013，24（4）：555- 563．

［6］Zhang S，Bar-Shalom Y．Track segment association for GMTI tracks of evasive move-stop-move maneuvering targets［J］．IEEE Trans.on Aerospace and Electronic Systems，2011，47（3）：1899 -1914．

［7］Pannetier B，Dezert J．Track segment association with classification information［C］∥Proc.of the Workshop on Sensor Data Fusion：Trends，Solution，Applications（SDF），2012：4- 6．

［8］Yu J G，Liu M，Chen J H．Ballistic target track segments association and optimization［J］．Acta Aeronautica et Astronautica Sinica，2011，32（10）：1894- 1904．（俞建国，刘梅，陈锦海．弹道目标航迹片段关联及优化［J］．航空学报，2011，32（10）：1897 -1904．）

［9］Han W，Tang Z Y，Zhu Z B．A method of tracking targets in Doppler blind zone based on multiple-hypothesis motion models［J］．Journal of Electronics&Information Technology，2013，35（3）：516- 523．（韩伟，汤子跃，朱振波．一种多普勒盲区条件下的多假设运动模型目标跟踪方法［J］．电子与信息学报，2013，35（3）：516- 523．）

［10］Zhang W，Liang Y，Lan H，et al．Track segments association for maneuver targets［J］．Computer&Digital Engineering，2013，41（3）：394- 398．

［11］He Y，Wang G H，Guan X．Information fusion theory with applications［M］．2nd ed．Beijing：Publishing House of Electronics Industry，2010：239- 242．（何友，王国宏，关欣，等．多传感器信息融合及应用［M］．2版．北京：电子工业出版社，2010：239- 242．）

［12］Aziz A M．A new nearest-neighbor association approach based on fuzzy clustering［J］．Aerospace Science and Technology， 2013，26（1）：87- 97．

［13］Aziz A M．A novel all-neighbor fuzzy association approach for multi-target tracking in a cluttered environment［J］．Signal Processing，2011，91（8）：2001- 2015．

［14］Aziz A M，Tummala M，Cristi R．Fuzzy logic data correlation approach in multisensor-multitarget tracking systems［J］．Signal Processing，1999，76（2）：195- 209．

［15］Weng C H，Chen Y L．Mining fuzzy association rules from uncertain data［J］．Knowledge and Information Systems，2010，23（2）：129- 152．

［16］Li B，Kang F J，Gao Y N．Kalman-filter-based track fitting in non-uniform magnetic field with segment-wise helical track model［J］．Computer Physics Communications，2014，185（3），754- 761．

［17］Kleinwort C．General broken lines as advanced track fitting method［J］．Nuclear Instruments and Methods in Physics Research A，2012，673（1），107- 110．

［18］He Y，Xiu J J，Guan X．Radar data processing with applications［M］．3rd ed．Bejing：Publishing House of Electronics Industry，2013：36- 62．（何友，修建娟，关欣．雷达数据处理及应用［M］．3版．北京：电子工业出版社，2013：36- 62．）

Track segment association algorithm based on multiple-hypothesis models with priori information

QI Lin1，2，WANG Hai-peng1，2，XIONG Wei1，DONG Kai1
（1.Institute of Information Fusion，Naval Aeronautical and Astronautically University，Yantai 264001，China；2.Key Lab for Spacecraft TT&C and Communication under the Ministry of Education，Chongqing 400044，China）

As tracks forecasting and associating accuracy of the traditional track segment association algorithms deteriorates seriously in maneuvering targets environment，a new algorithm based on multiple-hypothesis motion models with priori information is proposed．The algorithm firstly builds multiple-hypothesis motion models for tracks forecasting according to the priori information，for instance target property，target motion features，scenario condition，then describes the matching relations between forecasted old tracks and new tracks according to fuzzy correlation function on location and velocity information．Finally，the associated track segments on the basis of polynomial fitting connected．Simulation results showed that in the maneuvering targets scenario，the proposed algorithm remarkably outperformed the traditional track segment association algorithm．The proposed algorithm is suitable for complicated environment，after 50 times Monte Carlo simulation，when the break interval is less than 18，the average correct association rate of the maneuvering targets is more than 90%，and the global correct association rate is more than 85%．

track segment association（TSA）；priori information；multiple-hypothesis；fuzzy correlation function；tracks fitting

TN 95

A

10．3969／j．issn．1001-506X．2015．04．02

齐 林（1989-），男，博士研究生，主要研究方向为目标跟踪、多传感器信息融合。E-mail：3278pirate＠163．com

王海鹏（1985-），男，讲师，博士，主要研究方向为群目标跟踪、多传感器信息融合。E-mail：armystudent＠sohu．com

熊 伟（1977-），男，教授，博士，主要研究方向为状态估计、指挥自动化。E-mail：xiongweimail＠tom．com

董 凯（1986-），男，讲师，博士，主要研究方向为航迹关联、多传感器信息融合。E-mail：188dongkai＠163．com

1001-506X（2015）04-0732-08

2014- 08- 01；

2014- 09- 25；网络优先出版日期：2014- 10- 22。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141022．1320．004．html

山东省自然科学基金青年基金项目（ZR2012FQ004）；飞行器测控与通信教育部重点实验室开放基金（CTTC－FX201302）资助课题