基于RCB与锁相环的跟踪鉴别测向方法

任晓松，杨嘉伟，崔 嵬，吴嗣亮，安建波，欧春湘

（1．北京遥感设备研究所，北京100854；2．中国航天科工防御技术研究院，北京100854；3．北京理工大学信息与电子学院，北京100081）

基于RCB与锁相环的跟踪鉴别测向方法

任晓松1，杨嘉伟2，崔 嵬3，吴嗣亮3，安建波1，欧春湘1

（1．北京遥感设备研究所，北京100854；2．中国航天科工防御技术研究院，北京100854；3．北京理工大学信息与电子学院，北京100081）

为了弥补阵列天线导向矢量失配和相位测量噪声对测向性能的影响，提出一种基于稳健capon波束形成技术（robust capon beamforming，RCB）和锁相环的矢量最优估计与跟踪鉴别测向方法。首先基于RCB与锁相环原理，对目标来波信号导向矢量进行最优估计与跟踪测量；然后在稳定、准确跟踪导向矢量的基础上，借鉴扩频接收机伪码鉴相原理确定来波信号方向。仿真分析表明，该方法能够弥补阵列流型失配和相位噪声的影响、突破角度相关间隔的限制，准确测量来波信号的方向。

阵列信号处理；稳健波束形成；锁相环；角度鉴别；导向矢量；测向

0 引 言

相关干涉测向方法适用于多种阵列天线，具有测向准确度高的特点，在军事和民用领域中得到了广泛应用［1-2］。其基本原理是测量所接收信号在各阵元间的相位差，并与样本相位差进行相关运算，以代价函数最大方向作为来波信号方向的测量值。导向矢量与目标信号方向之间存在一一对应关系，与相关干涉测向方法中的相位差测量样本也存在对应关系，因此可以利用导向矢量的相关性进行测向。然而，在实际应用中阵列天线不可避免地存在各种误差（如阵元位置扰动误差、通道幅相误差）和相位噪声，这些因素会导致实际的阵列形式与理想状态存在偏差［35］，因此，如果简单基于相位差测量值构造与阵列相关的导向矢量，势必会影响到测向性能。

在过去30年里，有很多优秀的改善波束形成的稳健性方法，主要可分为基于特征空间的自适应波束形成、多点约束和对角加载技术等几类［6-10］，可以有效克服系统误差带来的不利影响，如信号被抑制、输出信干噪比下降等。文献［10］提出了基于不确定集的稳健波束形成方法（robust capon beamforming，RCB）；该方法将要估计的信号功率作为目标函数，在给定的误差范围内对导向矢量进行搜索，选择与波束形成输出功率的最大值对应的导向矢量作为真实导向矢量的估计，并用估计的导向矢量进行波束形成。该方法在提高信干噪比抑制系统误差等干扰的同时，对目标信号真实导向矢量实现了最优估计。因此，可以借鉴RCB原理，将最优估计得到的导向矢量应用到相关干涉测向方法中。

相关测向方法中角度的测量精度与相关角度间隔有关，角度间隔越小测量精度越高，但是角度间隔不能无限减小，并且角度间隔越小相关搜索带来的运算量越大。数字接收机锁相环（phase-locked loop，PLL）［11-14］直接对载波相位进行跟踪，通过鉴相器提取并输出相位估计误差，经过环路滤波器得到相位误差控制量，当环路稳定时具有较高的跟踪精度。而导向矢量与阵元相位差之间存在对应关系，并且在来波信号方向发生变化时，导向矢量与相位差同时产生对应变化；因此，可以借鉴数字接收机PLL原理对来波信号导向矢量从相位角度进行闭环跟踪测量。在环路锁定精确跟踪导向矢量之后，借鉴伪码跟踪环路鉴相器原理确定稳定跟踪环路的最终结果（导向矢量）所对应的角度，从而突破角度间隔限制、测量精度与相关搜索之间的矛盾。

仿真结果表明，本文提出的基于RCB与PLL的跟踪鉴别测向方法，不仅弥补了阵元位置扰动、通道幅相误差和相位噪声的影响，还突破了角度相关间隔与测量精度之间的矛盾。

1 阵列信号模型

假设K个窄带远场信号入射到M元均匀线阵（uniform linear array，ULA）上（K＜M），则t时刻阵列接收的数据为

式中，快拍矢量X（t）＝［x1（t），x2（t），…，xM（t）］T、噪声矢量N（t）＝［n1（t），n2（t），…，nM（t）］T均为M×1维的阵列接收数据；信号包络S（t）＝［s1（t），s2（t），…，sK（t）］T为K×1维，第i个信号为具有幅度α和初始相位φ的非随机信号，即

基于均匀线阵的导向矢量矩阵为A＝［a1，a2，…，aK］，其中，ai为与第i个来波信号对应的导向矢量，对应的来波方向为θi。基于阵元间距为d的均匀线阵和窄带来波信号si的阵列模型示意如图1所示。

图1 均匀线阵示意

以第一个阵元为参考阵元，则与等距线阵和si对应的导向矢量ai可表示为

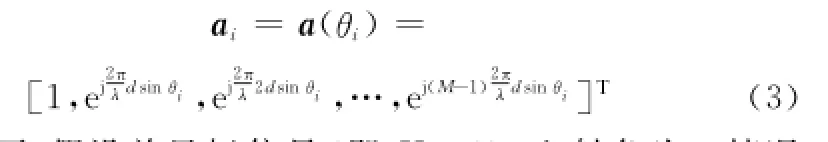
理想情况下，假设单目标信号（即K＝1）、入射角为θ情况下，根据式（2）和式（3）可以得出t时刻阵列接收的数据为

由于通道幅相误差和阵元位置扰动误差的存在，阵列接收的数据变为

可以记a～＝Γa，表示由于幅相误差和阵元位置扰动误差形成的真实导向矢量，其中

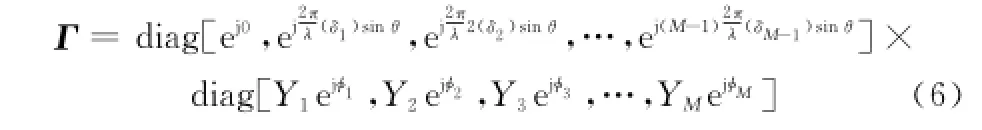
定义R＝E｛X（t）XH（t）｝为阵列接收信号的相关矩阵，其中，E｛·｝表示数学期望。

2 基于RCB与PLL的跟踪测向

2.1 算法提出

众所周知，对于确定的天线阵和目标信号，有式（1）和式（3）所示的接收信号模型和与目标信号方向有关的导向矢量，导向矢量与相关干涉测向方法中使用的相位差样本具有一一对应关系。可以借鉴相关干涉仪的测角原理［15－17］，选取导向矢量样本进行相关匹配处理，以相关序列极大值方向作为目标信号方向。

利用导向矢量进行目标信号方向的相关测量时，需要准确测量导向矢量，可以说来波信号导向矢量测量越准确，测向越精确。然而，由式（5）可知，接收信号受到通道幅相误差、阵元位置扰动等误差和噪声的影响，来波信号的导向矢量与理想导向矢量产生偏差；并且角度的估计精度与相关测向的角度间隔有关。

因此，为了弥补通道幅相误差和阵元位置扰动误差的影响，突破角度相关间隔的限制，消除噪声的影响，提高测向精度，借鉴RCB算法和PLL原理提出基于RCB与数字接收机PLL的设计方法。利用RCB对来波信号真实导向矢量进行最优估计；然后，将估计得到的导向矢量送给导向矢量闭环跟踪系统，使本地导向矢量始终跟随目标信号的导向矢量。在环路锁定之后，借鉴伪码跟踪环路鉴相器原理设计角度鉴别器，确定目标信号角度。

本文所提方法由3部分构成，分别是：基于RCB的导向矢量估计单元、基于PLL的导向矢量跟踪单元和角度鉴别单元。算法结构框图如图2所示。

2.2 基于RCB的导向矢量估计

基于接收到的快拍数据建立球形RCB［10］的优化模型为

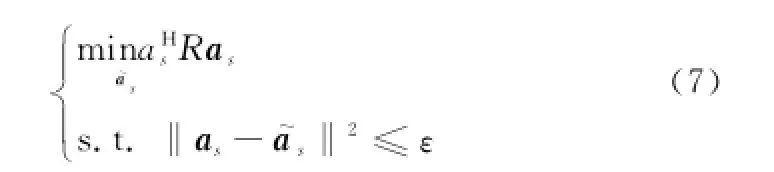
在式（8）约束下，可以避免平凡解as＝0的出现，除非ε＝（即此时as＝0位于约束集合的边界上）。对于式（8）中等式约束最优化问题，利用Lagrange乘数法进行有效求解有

式中，λL为Lagrange乘数。对as求导，并令其等于零，可得最优解利用矩阵求逆引理可得

图2 算法框图

最优Lagrange乘数λL可以利用牛顿迭代法通过求解约束方程g（λL）＝‖（I＋λLR）－1a～s‖2＝ε获得；然后代入最优权矢量表达式从而获得对目标信号真实导向矢量的最优估计值。

图3 RCB算法原理

式中，Γa为真实导向矢量；D＝diag［ejδ1，ejδ2，…，ejδM］为残留相位噪声引起的导向矢量偏差。

因此，基于RCB算法的导向矢量最优求解方法，初步弥补了通道幅相误差和阵元位置扰动误差的影响，抑制了相位噪声的影响，可以实现对目标信号真实导向矢量的估计。

2.3 导向矢量跟踪环路

为了进一步消除RCB算法估计所得导向矢量中残留相位噪声的影响，实现对来波信号导向矢量的动态跟踪，基于PLL原理提出导向矢量的闭环跟踪方法。跟踪环路主要由导向矢量鉴别器、环路滤波器和本地导向矢量数控振荡器（numerically controlled oscillator，NCO）3部分组成，组成如图2所示。鉴别器用于鉴别RCB估计导向矢量与本地导向矢量的复指数误差信号（与相位样本对应）；环路滤波器用于滤除导向矢量误差信号中的高频谐波分量，进一步滤除残留相位噪声的影响，对输入导向矢量进行精确估计；本地导向矢量NCO根据导向矢量初始值以及滤波器输出值，不断调整NCO的频率字保持对接收信号导向矢量的精确跟踪。

2．3．1 导向矢量鉴别

根据式（10）可知，与当前时刻来波方向对应的导向矢量估计值为

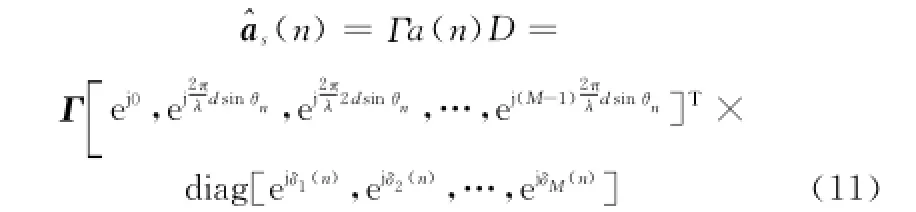
本地NCO产生的导向矢量为

式中，~D为本地NCO生成的初始导向矢量偏差，是D经环路滤波和NCO累加消除高频噪声所得。对式（12）取共轭，然后与式（11）相乘可得

式中

为来波信号角度变化引起的导向矢量偏差；

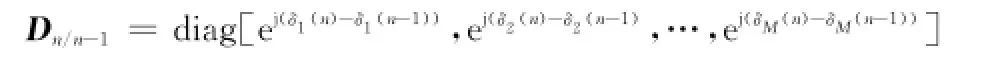
为相位噪声残差引起的导向矢量偏差。

2.3.2 环路滤波

与数字接收机载波PLL一样，导向矢量跟踪环路滤波器［12］的作用是滤除导向矢量误差信号中的高频谐波分量，使其在输出端保持对来波信号导向矢量的精确跟踪估计。

在角度变化不快的情况下，跟踪环路滤波器的阶数不需要太高，可以采用一阶环路滤波器。导向矢量跟踪环路滤波器设计如图4所示。

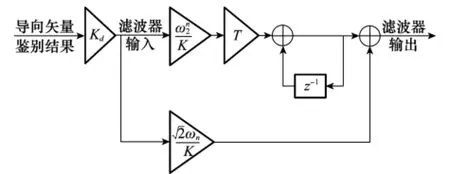
图4 导向矢量一阶滤波器数字实现

滤波器传递函数为式中，Kd为鉴频器增益；Ko为数控振荡器增益；K为环路增益；F（z）为环路滤波器转移函数；wn为自然频率；T为环路更新时间。

2.3.3 本地跟踪导向矢量NCO

本地跟踪导向矢量NCO根据环路滤波器的输出结果，不断调整NCO的频率字，保持对输入信号导向矢量的精确跟踪。导向矢量NCO的基本原理如图5所示。

图5 数控振荡器结构图

2.4 角度鉴别

在导向矢量跟踪环路锁定之后，借鉴伪码跟踪环鉴相器原理设计角度鉴别器，确定目标信号角度。以上一时刻本地导向矢量为中心，生成左偏和右偏角度θd／2的导向矢量；然后，分别计算左偏导向矢量与跟踪环路实时得到导向矢量之间的距离幅值pls，右偏导向矢量与跟踪环路实时得到导向矢量之间的距离幅值prs。基于导向矢量1范数进行归一化并取反加一操作之后的角度鉴别原理如图6所示。

图6 角度鉴别原理

基于本地导向矢量构造左偏角导向矢量和右偏角导向矢量为

左偏幅值与右偏幅值为

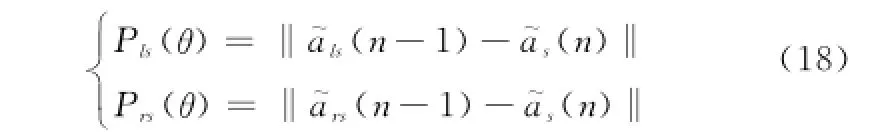
与幅值偏差对应的角度误差鉴别为

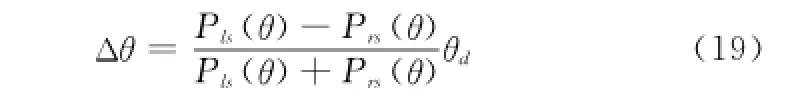
从而确定当前时刻测向结果为

式中，θ（n）和θ（n－1）分别代表当前时刻角度鉴别算法确定的来波信号方向和上一时刻的来波信号方向。

3 仿真结果与分析

设置仿真条件：天线为10阵元的均匀直线阵、每个阵元均为全向天线、理想状态下相邻阵元间距为半个波长。阵元通道间幅度误差服从均值为0，方差为0.1的高斯分布；相位误差服从均值为0，方差为20°的高斯分布。阵元位置扰动引起的d／λ服从均值为0．5，方差为0．03的高斯分布。

3.1 算法性能分析

在上述仿真条件下假设来波信号信噪比为15 dB，采样快拍数为40，目标来波信号方位向为－10°，对本文算法进行仿真分析如图7所示。基于RCB估计得到的导向矢量进行相关测向的结果如图7中虚线所示；利用锁相环路进一步消除导向矢量中高频干扰的测向结果如图7中实线所示，也即本文算法得到的最终测量值。可以发现，经过环路跟踪处理后，测量值更趋近于真实来波信号方向。

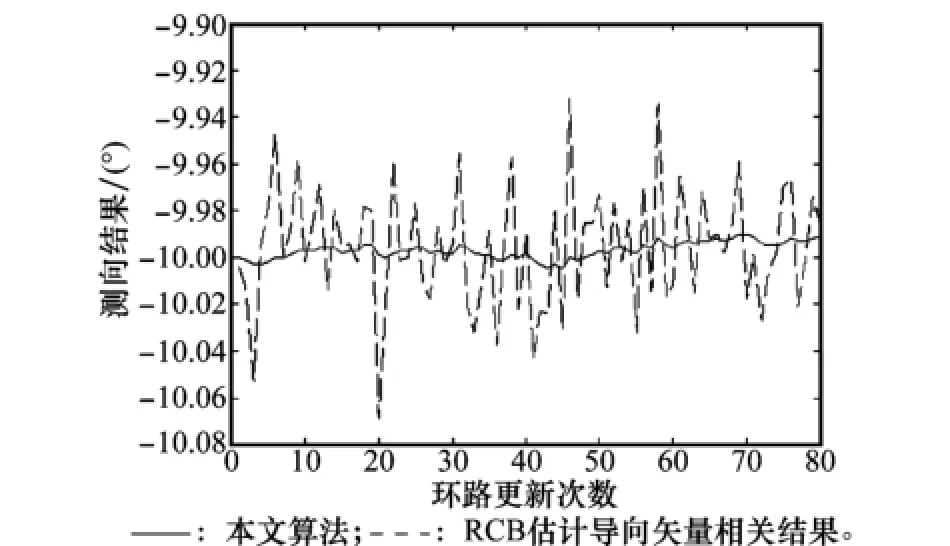
图7 算法性能对比示意

这说明本文提出的基于PLL的导向矢量闭环跟踪方法进一步消除了噪声干扰的影响，从而提高了测向精度。

在不同信噪比和采样快拍数条件下，对静态来波信号进行80次蒙特卡罗仿真，统计测角均方根误差如图8所示。可以发现，在相同信噪比情况下，随着快拍数增加，测角均方根误差具有逐渐减小的趋势；在相同采样快拍数情况下，随着信噪比增加，测角均方根误差具有逐渐减小的趋势；并且当信噪比达到20 dB时，采样快拍数的影响减小，测角均方根误差趋于一致。

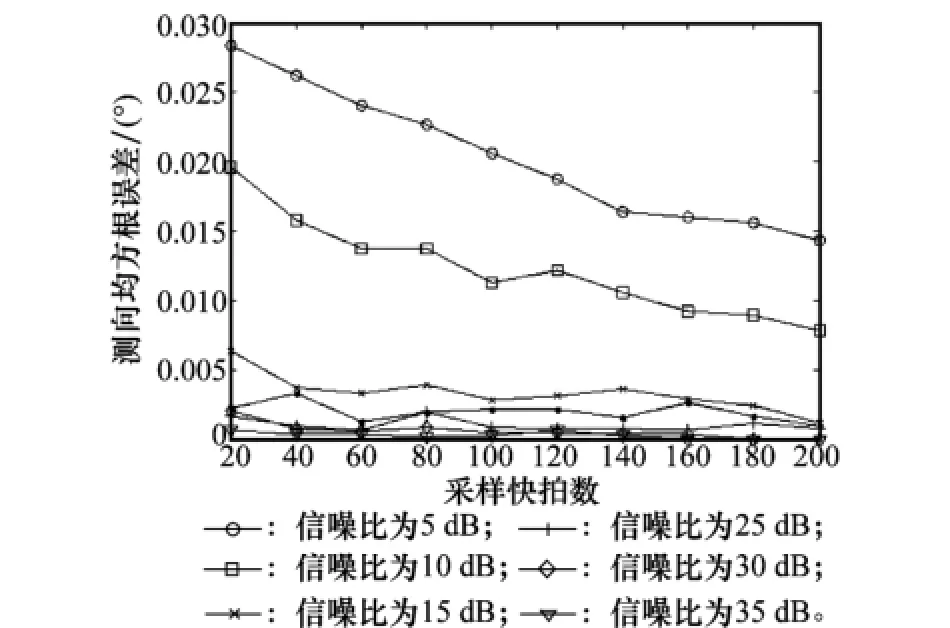
图8 影响测向因素分析

因此，利用本算法测量来波信号方向时，可以结合信噪比大小对采样快拍数进行调整，从而实现最优的参数配置。

3.2 静态仿真分析

在上述仿真条件下，设置来波信号信噪比为15 dB，采样快拍数为40；在［－10°，10°］区间内，以2°为间隔设置静态来波信号。利用本文方法、基于相位重构导向矢量的传统相关测向方法和基于RCB算法获得导向矢量进行相关测向的方法，对各个来波方向分别进行80次蒙特卡罗仿真，统计测向结果如图9所示。

可以发现，基于相位重构导向矢量的传统相关测向均方根误差数量级最大；利用RCB算法获得的导向矢量进行相关测向，其相关测向结果具有10－2数量级的测向精度；而本文算法则突破了角度相关间隔的限制，并具有较高的测向精度，达到了10－3数量级的测向精度。

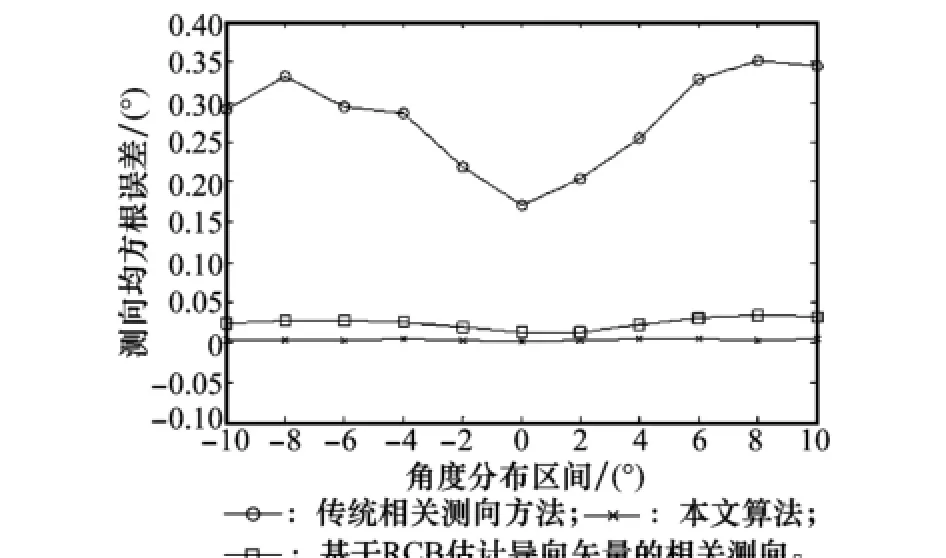
图9 静态测向均方根误差对比

3.3 动态仿真分析

设置目标信号入射角度范围为［－3°，3°］，以某项目为背景设置目标信号以5（°）／s的角速度匀速运动；来波信号信噪比为15 dB，采样快拍数为40。利用本文算法可以实现对来波信号的稳定跟踪，环路稳定跟踪动态来波信号角度仿真结果如图10所示。

图10 动态测向示意

利用本文方法在［－3°，3°］区间范围内对动态来波信号进行80次蒙特卡罗仿真，统计测向结果，并与基于相位重构导向矢量的传统相关测向方法和基于RCB算法获得导向矢量进行相关测向的结果进行比较，如图11所示。动态仿真表明，本文算法能够对来波信号的角度变化进行稳定跟踪测量，具有较高的测量精度。

图11 动态测向均方根误差对比

4 结 论

本文所提方法，首先利用RCB算法对来波信号导向矢量进行最优估计；为了进一步消除系统噪声的影响，基于PLL原理实现了对来波信号导向矢量的准确跟踪测量。基于接收机伪码跟踪环路鉴相器原理设计的角度鉴别器，有效突破了角度相关间隔的限制。通过仿真分析表明，该方法弥补了阵列天线系统误差和测量相位随机噪声的影响，可以实现来波信号方向的高精度测量。

［1］Kebeli M．Extended symmetrical aperture direction finding using correlative interferometer method［C］∥Proc.of the 7th IEEE International Conference on Electrical and Electronics Engineering，2011：209- 213．

［2］Wei H W，Shi Y G．Performance analysis and comparison of correlative interferometers for direction finding［C］∥Proc.of the 10th IEEE International Conference on Signal Processing，2010：393- 396.

［3］Zhu L Y，Meng H E，A robust minimum variance beamformer with new constraint on uncertainty of steering vector［J］.Signal Processing，2006，86（9）：2243- 2254.

［4］Jiang X，Zeng W J，Yasotharan A，et al．Robust beamforming by linear programming［J］.IEEE Trans.on Signal Processing，2014，62（7）：1834- 1849.

［5］Robert G L，Stephen P B．Robust minimum variance beamforming［J］.IEEETrans.on Signal Processing，2005，53（5）：1684- 1696.

［6］Ruan H，De L，Rodrigo C．Robust adaptive beamforming using a low-complexity shrinkage-based mismatch estimation algorithm［J］. IEEESignal Processing Letters，2014，21（1）：60- 64.

［7］Vorbyov S A，Gershman A B，Luo Z Q．Robust adaptive beamforming using worst case performance optmization a solution to the signal mismatch problem［J］.IEEE Trans.on Signal Processing，2003，51（2）：313- 324.

［8］Elnashar A，Elnoubi S M，El-Mikati H A．Further study on robust adaptive beam forming with optimum diagonal loading［J］. IEEE Trans.on Antennas Propagation，2006，54（12）：3647- 3658.

［9］Gong C，Huang L，Xu D，et al．Knowledge-aided robust adaptive beamforming with small snapshots［J］.Electronics Letters，2013，49（20）：1258- 1259.

［10］Li J，Stoica P，Wang Z S．On robust Capon beamforming and diagonal loading［J］.IEEE Trans.on Signal Processing，2003，51（7）：1702- 1715.

［11］Hu H，Sun H Z，Ji，Z Y．Study on algorithm and control strategies of GPS carrier tracking loop under high dynamic condition［J］.Journal of Astronautics，2011，32（8）：1805- 1812．（胡辉，孙函子，纪兆云．高动态GPS载波跟踪算法和环路控制策略研究［J］．宇航学报，2011，32（8）：1805- 1812．）

［12］Kaplan E D．Understanding GPS principles and applications［M］．Boston：Artech House，1996．

［13］Ravindra B，Jinling W．Dynamics performance of carrier and code tracking loops in ultra-tight GPS／INS／PL integration［C］∥Proc.of the IEEE India Conference，2005：233- 236.

［14］Roncagliolo P A，Cristian E D B，Carlos H M．GPS digital tracking loops design for high dynamic launching vehicles［C］∥Proc.of the 9th IEEE International Symposium on Spread Spectrum Techniques and Applications，2006：41- 45．

［15］An X J．Research on DF based on improved phase interferometer［J］.Radio Engineering of China，2009，39（3）：59- 61．（安效君．改进的干涉仪测向方法研究［J］．无线电工程，2009，39（3）：59- 61．）

［16］Wu Y W，Rhodes S，Satorius E H．Direction of arrival estimation via extended phase interferometry［J］.IEEE Trans.on Aerospace and Electronic Systems，1995，31（1）：375- 381．

［17］Xiao X L．The theory of interferometer in DOA［J］.China Radio，2006，（5）：43- 49．（肖秀丽．干涉仪测向原理［J］．中国无线电，2006，（5）：43- 49．）

Tracking and discriminating direction finding method based on robust capon beamforming and phase-locked loop

REN Xiao-song1，YANG Jia-wei2，CUI Wei3，WU Si-liang3，AN Jian-bo1，OU Chun-xiang1
（1.Beijing Institute of Remote Sensing Equipment，Beijing 100854，China；2.China Aerospace Defense Technology Institute，Beijing 100854，China；3.School of Information and Electronics，Beijing Institute of Technology，Beijing 100081，China）

In order to compensate the impact of the antenna array steering vector mismatch and the phase measurement noise，the optimal measurement method is proposed for steering vector，and the tracking identification method of direction finding is designed，basing on the robust capon beamforming（RCB）and phase-locked loop．Firstly，using the RCB algorithm estimate the optimal signal steering vector，and then basing on the principle of phase-locked loop to closed-loop track target signal steering vector．After steady and accurate tracking of the steering vectors，referencing the principle of spread spectrum receiver pseudo-code phase detector，the direction of the target signal is determined．Simulation results show that the proposed method can compensate the impact of the steering vector mismatch and phase measurement noise，break through the restrictions of the angle correlation interval，and accurate measure the target signal direction．

array signal processing；robust beamforming；phase-locked loop（PLL）；angle identification；steering vector；direction finding

TN911

A

10．3969／j．issn．1001-506X．2015．04．04

任晓松（1981-），男，工程师，博士研究生，主要研究方向为阵列信号处理、雷达信号处理。E-mail：lengyunrxs＠163．com

杨嘉伟（1963-），男，研究员，博士，主要研究方向为雷达系统。E-mail：yjw＠163．com

崔 嵬（1974-），男，研究员，博士，主要研究方向为遥测遥控。E-mail：cuiwei＠bit．edu．cn

吴嗣亮（1964-），男，研究员，博士，主要研究方向为雷达技术。E-mail：siliangwu＠bit．edu．cn

安建波（1976-），男，高级工程师，硕士，主要研究方向为制导控制。E-mail：anjianbo＠163．com

欧春湘（1988 ），女，工程师，博士研究生，主要研究方向为卫星导航。E-mail：ouchunxiang＠163．com

1001-506X（2015）04-0746-06

2014- 05- 28；

2014- 10- 26；网络优先出版日期：2014- 11- 26。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141126．1439．001．html