基于随机阵列的NUFFT BP三维快速成像

向 高，张晓玲，吴宗亮

（电子科技大学电子工程学院，四川成都611731）

基于随机阵列的NUFFT BP三维快速成像

向 高，张晓玲，吴宗亮

（电子科技大学电子工程学院，四川成都611731）

传统的二维实阵列用于三维微波成像时，需要相对较高的脉冲重复频率才能切换发射阵元。针对这种情况，利用随机阵列来实现三维成像，目的是有效降低脉冲重复频率。进一步提出利用等效相位中心原理来实现任意随机阵列布局的可行性方案。然后，基于随机阵列，发现使用非均匀快速傅里叶变换（nonuniform fast Fourier transform，NUFFT）来实现后向投影（back projection，BP）算法的插值过程，能够用较少的运算量实现BP算法的高精度插值。最后，结合并行处理技术来实现NUFFT BP算法，结果使得BP算法的执行效率得到显著提高。

随机阵列；非均匀快速傅里叶变换；并行处理；后向投影

0 引 言

传统的二维实阵列用于三维微波成像时，主要有均匀满阵元方式和天线单元曲线运动合成面阵［1］两种方式。对于满阵元方式，除了成本高以外，当要求所有阵元都要收／发信号的时候，需要很高的脉冲重复频率（pulse repetition frequency，PRF）来实现切换阵元。同时，运动合成面阵容易受到阵元机械运动的影响，例如：存在平台晃动，需要较长的运动合成时间等。

为了解决上述问题，本文提出使用随机二维阵列进行三维微波成像。尽管文献［2］等已经提出了随机阵列成像的概念，但是并未给出合理的随机阵列布局的生成方案。文献［3- 4］虽然都利用等效相位中心（phase center approximation，PCA）原理来等效均匀阵列，然而该等效阵列仅仅只是一维的。文献［5］将PCA原理进一步推广到了二维阵列，实现了多输入多输出（multiple input multiple output，MIMO）阵列的等效均匀二维阵列。本文正是以这种等效均匀二维阵列为基础，实现了任意构型的随机二维阵列。本文以“十”字形布阵为基础，分析了随机阵列的随机阵元数目的选择。由于随机阵列其阵元位置的不确定性，所以无法使用距离 多普勒［67］（range-Doppler，RD）等传统算法进行聚焦，因此提出使用Type-Ⅱ型非均匀快速傅里叶变换（nonuniform fast Fourier transform，NUFFT）［8］插值的后向投影（back projection，BP）算法进行聚焦，并利用并行计算架构［9－10］（compute unified device architecture，CUDA）实现了距离历史和NUFFT插值的并行运算。

1 随机二维阵列

随机二维阵列其阵元在阵列平面内的均匀网格上随机分布，如图1所示。当这些随机阵元不共线时，即可以产生空间二维角分辨率［2］，再结合脉冲压缩技术，则能够实现三维微波成像。如何合理地选择随机二维阵列的构成方案，这是主要考虑的问题。因此，本节提出了一种合理可行的随机二维阵列的构成方案，并给出了合理的随机阵元数目的选择方法。

图1 随机二维阵列成像的几何构型

1.1 随机二维阵列的布局设计

如果采用直接随机布置阵元的方式来实现随机二维阵列，不仅成本高，难于实现，而且无法灵活改变阵元位置的分布，结果使得其实用性大大降低。因此，可以考虑利用虚拟阵元的方式来实现随机二维阵列。图2展示了一种基于二维MIMO阵列来实现虚拟随机二维阵列的布局方案［5］，该方案基于PCA原理来实现虚拟二维均匀阵列，此时只要激活合适的收发阵元，就可以很容易地获得任意构型的随机二维阵列。简要叙述PCA原理：可以用一个虚拟的天线单元，等效出位置上分置的发射天线和接收天线两者的功能，该虚拟天线单元同时具有收／发功能，并且位于分置的收发天线两者连线的中心。

图2 MIMO二维面阵

简单分析图2中是如何实现虚拟二维均匀阵列。图2使用了端发“密疏密”布阵模式［4］，能够很好地利用阵列长度。在阵列平面的Ⅰ、Ⅱ、Ⅲ和Ⅳ区域布置发射阵元，用符号T表示，发射阵元沿x轴间距为dxT，沿y轴间距为dyT，发射阵元沿x轴和y轴数目记为MaT，要求其为偶数，那么总的发射阵元数目为MT＝M2aT；在阵列平面中心区域布置接收阵元，用符号R表示，接收阵元沿x轴间距为dxR，沿y轴间距为dyR，接收阵元沿x轴和y轴数目记为MaR，那么总的接收阵元数目为MR＝M2aR；最邻近的发射阵元和接收阵元沿x轴和y轴的间距分别为dxTR和dyTR。如果上述阵元间距dxT、dyT、dxR、dyR、dxTR和dyTR满足约束关系：dxT＝2da、dyT＝2da、dxR＝daMa／2、dyR＝daMa／2、dxTR＝da和dyTR＝da，那么就可以获得一个虚拟的二维均匀阵列，此时该虚拟阵列沿x轴和y轴的间距都为da；虚拟阵元沿x轴和y轴的数目都为Ma。最终，可以用MT＋MR个阵元获得MaTMaR×MaTMaR的虚拟的二维均匀阵列，该虚拟阵列边长为La＝（n－1）da，且n＝MaTMaR。

在三维成像时，可以采用多发多收模式：被选中的发射单元同时发射不同中心频率的宽带信号，被选中的接收单元接收所有回波，然后在信号处理端通过数字滤波来获得相应的基带信号。然而，此时需要采集端有较大的带宽才能同时接收所有发射阵元的回波，否则，只能采用单发多收模式。相对于多发多收模式，单发多收模式可以灵活地控制和激活所需要的收发阵元，并能降低系统功耗。根据PCA原理，在单发多收模式下，一个发射阵元可以获得与之对应的多个虚拟阵元，并且每个虚拟阵元同时具有收／发功能。因此，与传统二维阵列相比，单发多收模式下随机二维阵列所需要的PRF大大降低。

1.2 随机阵元数目的选择

已经分析了如何实现虚拟随机二维阵列，为了简化分析，后文的讨论都是建立在第1.1节等效后的虚拟随机二维阵列的基础之上。然而，如何确定合适的随机阵元数目，才能够保证有较高质量的三维微波成像效果呢？

文献［2］定义了随机阵列沿指定方向的模糊函数，该模糊函数主要取决于随机阵列沿指定方向上的投影。为了保证阵列具有三维分辨能力和能够充分利用阵列的长度，必须要求这些随机阵元能够在一对相互正交的方向上投影出满阵列，这样就可以在这一对正交方向上获得与等效均匀线阵相当的聚焦能力。例如，有若干个随机阵元在阵列平面中心沿着x轴和y轴分布，这样就可以构成一个“十”字形正交阵列。显然，要获得更好的三维成像能力，则随机阵元的数目Na不能少于2n－1。从N＝（MaTMaR）2个阵元网格中随机选取Na个位置来布置阵元，那么能够满足投影要求的排列的概率可以表示为

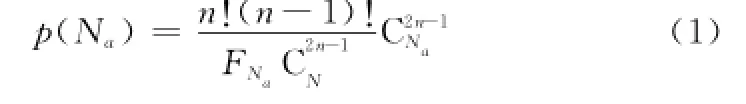
式中，FNa∈R＋表示重复度，并且是关于Na的非线性函数。从物理意义上分析，当Na增大时，随机阵元能够覆盖的“十”字形阵列的可能性就越大，即p（Na）是关于参数Na的单调不减函数。FNa在实际中很难确定，如果令其取1，则可以获得Na＜N时函数p（Na）的上界；而当Na＝N时，p（Na）≡1。由此，可以得到

由式（2）可以估计出使p（Na）满足给定概率门限的Na的值。一般取Na为n的整数倍，如果成像效果不理想，可以逐步提高倍数。实验发现当Na约占20%的网格时，就能取得较好的成像效果。

当N较小时，可以通过仿真实验来确定合适的Na值。如图3所示，通过2万次蒙特卡罗仿真试验，可以绘制出大概的p（Na）曲线，其步骤如下：

步骤1 生成随机阵元位置序列，然后向x和y方向进行投影；

步骤2 统计存在空行、空列以及同一阵元在x和y方向都被投影的情况。然后就可以绘制出p（Na）的曲线。

图3 不同阵元间隔时p（Na）曲线

2 随机二维阵列的三维微波成像

2.1 信号模型

假定随机阵列工作在单发多收模式下，等效后的随机阵列如图1所示。尽管在一个PRF内可以获得多个阵元的数据，但是为了描述方便，假设在每个PRF内，只有第i（i＝0，1，…，Na－1）个阵元Γi收／发信号，用符号t表示快时间，那么，对于观测场景Ω中任一散射目标P∈Ω其回波为

式中，I（P）表示散射目标P的散射系数；wa（Γi）表示阵列对Γi的加权，可假设为1；pr［·］表示发射的线性调频信号的波形；R（P，Γi）＝2‖P－Γi‖2表示双程距离历史；c表示电磁波传播速度；λ为发射信号波长。那么，对于整个观测场景Ω，阵元Γi∈Ξ（Ξ＝，观测到的回波可以表示为

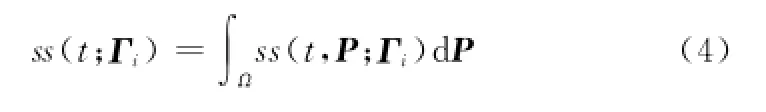
2.2 BP算法简介

由于随机二维阵列的阵元是随机选择的，所以其不再适合利用传统的RD算法［6-7］、线频调变标（chirp scaling， CS）算法［1112］等进行微波成像。由于BP算法［1315］适合于任意的天线相位中心轨迹，因此，BP算法成为最合适的选择。首先对回波信号进行距离压缩，那么压缩后的时域信号可以表示为BP算法的实质是时域相关积累。于是，只需要对阵元Γi的回波进行目标Q∈Ω的相位补偿，便可以得到Q的单阵元图像（Q；Γi）为

式中，tQ（Γi）＝R（Q，Γi）／c，表示目标Q和阵元Γi之间的回波延迟。最终，将所有单阵元的图像进行累加，就可以得到目标Q的BP成像结果为

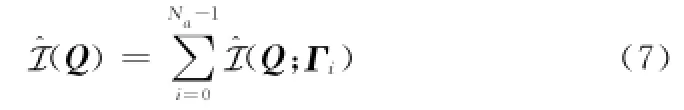
在这里需要强调的是，ssc（tQ（Γi）；Γi）需要利用插值计算来完成。在传统的BP成像算法中，插值计算使用辛克函数插值［15］。在后文中，将使用NUFFT［8，16-18］来实现该插值过程。

3 NUFFT BP及加速实现

由于R（Q，Γi）相对于目标Q而言是非均匀的，所以无法直接利用传统的快速傅里叶变换（fast Fourier transform，FFT）来快速求解ssc（tQ（Γi）；Γi）。然而，Type-ⅡNUFFT恰好能够实现从均匀频域数据插值得到高精度的非均匀时域数据。因此，本节利用快速高斯栅格的Type-ⅡNUFFT［8］来完成ssc（tQ（Γi）；Γi）的高精度插值。

3.1 NUFFT BP算法的提出

对于选定的阵元Γi，利用一维Type-ⅡNUFFT可以同时实现对成像空间中所有的时间节点tQ（Γi）进行插值。根据离散时间信号理论，ssc（tQ（Γi）；Γi）可用离散傅里叶变换进行求解，即

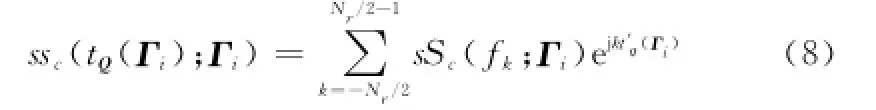
式中，sSc（fk；Γi）＝F［ssc（t；Γi）］，表示ssc（t；Γi）的傅里叶变换；fk为快时间频率；t′Q（Γi）＝2πFstQ（Γi）／Nr，表示将tQ（Γi）归一化到［0，2π］，Nr为距离向采样点数；Fs为回波信号的采样频率。

定义辅助函数ssc，－τ（t；Γi）为

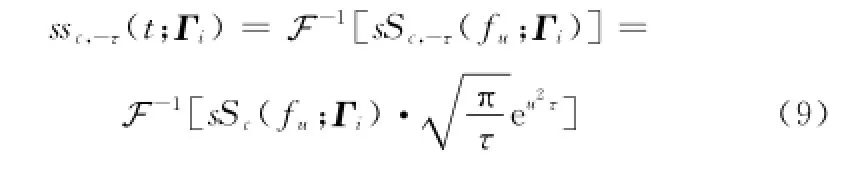
式中，F－1［·］表示逆傅里叶变换；u＝0，1，…，Mτ－1，Mτ＝2Nr为辅助函数的点数。然后，利用高斯核函数（x∈［0，2π］）对辅助函数ssc，－τ（t；Γi）进行插值，从而就可以得到ssc（tQ（Γi）；Γi），即

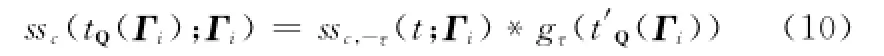
式中，符号*表示卷积。

通常τ非常小，所以式（10）中的高斯核函数为类脉冲函数，实际中其截断长度选择为2Msp即可，其中Msp表示截断的高斯核函数的一半的点数。当Msp＝6时，NUFFT可以获得6位数值精度，而Msp＝12时，则可以获得12位数值精度［8］。具体在操作时，参数τ的取值通常选择为Msp／N2r。在本节中，由于BP算法的具体实现过程最终是由NUFFT插值来完成的，所以称这种BP算法为NUFFT BP算法。

3.2 CUDA加速实现

虽然，上述的NUFFT算法快速实现了ssc（tQ（Γi）；Γi）的插值。但是，当成像空间的点数增多时，求解R（Q，Γi）的计算量仍然很大。例如，对60×60×60点（21.6万点）的区域进行成像时，对于阵元Γi需要计算21.6万次R（Q，Γi）。利用图形处理单元（graphics processing unit，GPU）并行计算技术，可以将求解R（Q，Γi）并行化，同时NUFFT插值也可以进行并行处理，从而能够使得BP成像处理效率得到进一步提高。CUDA加速的NUFFT BP成像过程可以用如图4所示的伪代码进行描述。

图4 CUDA加速的NUFFT BP

图4 中，核函数cuda_Range HistoryQGamma用来求解Γi和场景中所有像素点的距离历史；核函数cuda_Nu FFTInterp完成距离历史归一化插值时间节点和NUFFT插值过程；核函数cuda_Phase Compensation And Accumulation完成相位补偿和积累操作。

需要强调的是，用CUDA来加速NUFFT时，能够实现的点数受CUDA能够实现的FFT的最多的点数（约226复数点）和GPU全局内存大小的限制［19］。由于成像过程中不止NUFFT占用GPU内存，所以通常假设成像时NUFFT处理的点数不超过800万点。当成像区域像素点数大于这一限制时，需要对成像区域进行适当地划分再处理。把用CUDA加速实现的NUFFT BP成像过程简称为CUDA NUFFT BP。

3.3 运算量分析

本小节对传统BP算法（使用辛克函数插值），NUFFT BP算法和CUDA NUFFT BP算法的运算量进行简要分析。由于乘法运算和开方运算对执行效率影响较大，故分析时主要考虑乘法运算和开方运算的运算量。

如图4所示，NQ表示整个成像空间的像素点数，sX、sY和sZ分别表示成像空间的沿x轴、y轴和z轴的像素点数，于是NQ＝sX×sY×sZ。辛克函数插值核点数用MBP表示，NQ点数据开方操作的运算量为Osq（NQ）。

传统BP算法的运算主要由距离压缩（包括FFT、频域相乘和逆快速傅里叶变换（inverse fast Fourier transform，IFFT））、距离历史计算（包括乘法和开方运算）和辛克函数插值（查表实现）构成。于是，传统BP算法的运算量大约为

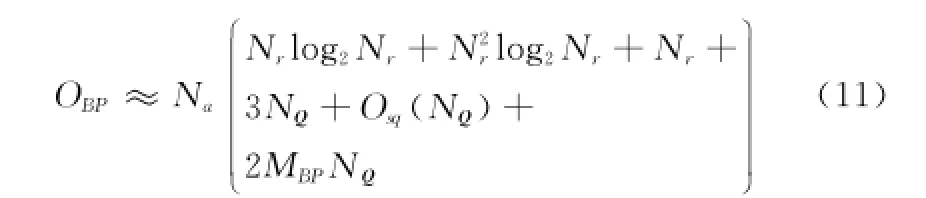
如果采用直接计算辛克函数的值，那么插值操作的运算量大约为10MBPNQNa。

NUFFT BP算法的运算主要包括计算频域距离压缩数据，距离历史计算以及NUFFT插值。其中，直接计算频域距离压缩数据，可以省掉IFFT的运算量；同时，逐阵元方式还可以有效降低距离历史计算的运算量。于是，NUFFT BP算法的运算量大约为

CUDA NUFFT BP算法为了便于并行化处理，其距离历史计算和传统BP算法一样，其余运算量同NUFFT BP算法。那么，CUDA NUFFT BP算法的运算量大约为

观察式（11）～式（13）可以发现，当成像的像素点数NQ较大时，3种算法的运算量主要取决于插值运算和距离历史计算。其中，NUFFT BP算法的运算量和传统BP算法用查表实现时基本相当，且低于直接计算辛克函数的值的方式；同时，NUFFT插值精度也远优于辛克函数插值。

4 仿真实验

本节利用计算机仿真实验来验证随机二维阵列实现三维微波成像的可行性。同时，本节也进行了CUDA加速的NUFFT BP的性能实验。实验中，设置9个点目标，它们的位置分别为（0 m，0 m，0 m）、（30 m，－30 m，10 m）、（－30 m，30 m，10 m）、（－30 m，－30 m，10 m）、（30 m，30 m，10 m）、（30 m，－30 m，－10 m）、（－30 m，30 m，－10 m）、（－30 m，－30 m，－10 m）和（30 m，30 m，－10 m）。其他主要参数如表1所示。

表1 阵列参数和波长

4.1 阵列成像对比实验

图5 不同阵元分布及其三维成像结果

图5 展示了4种不同的阵列布局方案，以及它们对应的9个点目标的三维成像结果（10 dB动态范围）。从图5（a）和图5（e）可以看出，“十”字形阵列布局尽管可以实现目标三维聚焦，但是对于非中心点目标，旁瓣非常明显。当阵元数目增加构成“米”字形阵列时，旁瓣效应明显减弱，但是在邻近目标的几个分辨单元内旁瓣依然较强，如图5（b）和图5（f）所示。利用和“米”字形阵列数目（4n－3个）相近的随机阵元（4n个）成像，如图5（c）和图5（g）所示，其成像结果虽然也会散布一些非目标强散射单元，但相比“米”字形阵列成像结果，它们在成像空间里更分散，强度更弱。而当使用满阵元进行成像时，就得到非常理想的成像结果，如图5（d）和图5（h）所示。

进一步对点目标成像性能进行分析。分别取占全部阵元20%、40%和100%的阵元数目对目标点（0，0，0）进行成像，并沿着y轴作该点目标的一维剖面图，结果如图6所示。由图6可以发现，在上述3种情况下，剖面图的主瓣宽度几乎一致，因此其分辨率基本相同（约29．2 m）。这是因为足够数目的随机阵元在阵列平面内均匀随机分布，能够在x轴和y轴方向都投影出满阵元线性阵列，所以使得3种情况的有效阵列长度均相同，从而它们的分辨率基本一致。由图6还可发现，上述3种情况的峰值旁瓣比也基本相同（约－13．3 dB）。

图6 不同数目随机阵元时点目标剖面图

需要注意，图6并不能反映出积分旁瓣比的性能，因为阵列天线产生的是角分辨率，这造成点目标的旁瓣会向阵列方向发生弯曲，如图5（e）所示。然而综合图5和图6可知，积分旁瓣比随着所选用的阵元数目的增加可以得到不断改善，最终达到和满阵元时一致。

由图5和图6，容易发现，当阵元均匀随机分布时，只要选择适当数目的随机阵元，就能使目标的三维聚焦效果和满阵元时相当；当阵元数目增加时，其聚焦效果也逐步逼近满阵元的结果。在实验过程中还可以得出如下结论：一般地，当随机阵元数目占总网格数的18%～20%时，已经可以有很好的三维聚焦效果（10 d B动态范围）。这意味着即使在使用满阵元成像时，也可以先利用20%的阵元聚焦，然后提取10 d B动态范围，再积累剩余阵元的数据，这样操作大约可以提高3～5倍的成像效率。

4.2 NUFFT插值精度实验

本小节比较NUFFT插值和辛克函数插值的插值精度。其中，NUFFT插值核长度为12；辛克函数插值核长度为16，并采用直接计算辛克函数的值的方式。选择某一阵元数据，对1 331个插值节点使用这两种方法分别插值。精确的插值结果则按式（8）用距离压缩频域数据进行离散傅里叶变换得到。图7展示了利用离散傅里叶变换精确插值的结果，以及辛克函数插值和NUFFT插值的误差。

图7 辛克函数插值和NUFFT插值的误差

由图7可以发现，辛克函数插值的误差分布在0～1；而NUFFT插值的误差则分布在0～4×10－6，这和前文提到的6位数值精度是一致的。上述实验结果表明12点NUFFT插值的精度远远优于16点辛克函数插值。根据前文运算量分析可知，12点NUFFT插值所需要的运算量也远低于16点辛克函数插值。

4.3 CUDA性能实验

为了充分验证算法的性能和有效性，本节选择两台不同配置计算机进行实验。计算机I运行环境如下：操作系统为Windows 7 64bit，Matlab 2012b，Intel i5－3550 CPU（3．30GHz），内存8G，Nvidia GeForce GTX 670以及CUDA 5．5。计算机Ⅱ的运行环境如下：Windows 7 64bit，Matlab 2012b，Intel i5－2320 CPU（3GHz），内存12G，Nvidia GeForce GT 560Ti以及CUDA 5．5。

根据前文的分析可以知道，CUDA NUFFT BP按逐阵元方式批量处理成像区域的所有像素点，所以，要处理的像素点越多，就更能体现出CUDA的优势。设计两组实验，利用满阵元方式成像，分别选择61×61×61点（实验Ⅰ）和121×121×121点（实验Ⅱ）的成像区域。利用Matlab的GPU并行处理功能实现距离历史计算的NUFFT BP称为Matlab GPU NUFFT BP。考察4种BP成像方法：传统BP、NUFFT BP、Matlab GPU NUFFT BP和CUDA NUFFT BP。需要说明的是，前3种方法是利用Matlab实现的；传统BP的插值为辛克函数插值；而其余方法都是利用NUFFT来实现BP的插值过程。另外，由于Matlab对于循环计算执行效率很低，这直接影响了距离历史计算和辛克函数插值的效率，不能真实反映算法本身的运算量。因此，本文将距离历史计算和辛克函数插值都采用C语言实现，然后由Matlab进行调用；并且辛克函数插值也采用批量计算插值方式，而不是循环逐点插值方式。

由表2可以看出，当成像搜索区域有226 981点（实验Ⅰ）时，与传统BP相比，利用NUFFT插值的BP都在一定程度上节约了计算时间，而CUDA NUFFT BP的加速效果则更为显著。对于CUDA NUFFT BP，计算机Ⅰ加速倍数约为31倍，计算机Ⅱ加速倍数约为22倍。两台计算机的CUDA NUFFT BP性能不同，主要是和它们的GPU并行计算能力有关。

表2 CUDA性能实验Ⅰ结果

当像素点数增加到1 771 561点（实验Ⅱ）时，利用CUDA并行计算距离历史的优势就更为明显，如表3所示。由于Matlab利用GPU并行求解距离历史涉及到频繁的内存拷贝，所以Matlab GPU NUFFT BP的效率提高地并不显著。对于计算机Ⅰ，其CUDA NUFFT BP相对于Matlab GPU NUFFT BP的加速倍数达到了约20倍；而计算机Ⅱ也有约13倍的加速倍数。

表3 CUDA性能实验Ⅱ结果

综合表2和表3，可以得出如下结论：NUFFT插值能够提高BP成像算法插值过程的效率；由于CUDA NUFFT BP并行实现了计算距离历史以及并行实现了NUFFT，从而显著地加速了BP成像算法的执行效率。

5 结 论

本文首先利用随机二维阵列进行三维微波成像，降低了对PRF的要求和系统功耗。然后，基于等效相位中心原理，本文提出了一种利用二维MIMO阵列天线等效虚拟随机二维阵列的方法，结果降低了阵列成本，同时因为该方法容易实现任意随机分布的二维阵列，所以又增强了阵列设计的灵活性。研究结果表明，通过TypeⅡNUFFT实现BP的插值过程，可以使得BP的计算效率得到一定程度地提高，而利用CUDA并行运算又能够进一步地提高BP的计算效率。最后，仿真实验证实了利用随机二维阵列进行三维微波成像的有效性和可行性，其中，NUFFT BP的插值精度要远优于传统BP的辛克函数插值的插值精度，并且在算法性能方面，CUDA NUFFT BP相对于传统的BP算法也有极大地提升。另外，CUDA NUFFT BP不仅适用于随机二维阵列的三维成像，而且还可以推广到其他任意合成孔径雷达的成像模式之中。

［1］Shi J，Zhang X L，Yang J Y，et al．APC trajectory design for“one-active”linear-array three-dimensional imaging SAR［J］. IEEE Trans.on Geoscience and Remote Sensing，2010，48（3）：1470- 1486.

［2］Shi J，Zhang X L，Xiang G，et al．Signal processing for microwave array imaging：TDC and sparse recovery［J］.IEEE Trans. on Geoscience and Remote Sensing，2012，50（11）：4584- 4598.

［3］Ender J H，Klare J．System architectures and algorithms for radar imaging by MIMO-SAR［C］∥Proc.of the IEEE Radar Conference，2009：1- 6.

［4］Xie W C，Zhang X L，Shi J．MIMO antenna array design for airborne down-looking 3D imaging SAR［C］∥Proc.of the IEEE International Conference on Signal Processing Systems，2010：452- 456.

［5］Zhang X L，Xiang G，Shi J．An implementation of sparse MIMO array for radar antenna［P］．China：201210000517，2013- 06-12．（张晓玲，向高，师君．一种稀疏MIMO平面阵列雷达天线构建方法［P］．中国：201210000517，2013- 06- 12．）

［6］Wu Q S，Zhang Y D，Amin M G，et al．Focusing of tandem bistatic SAR data using range Doppler algorithm［C］∥Proc.of the IEEE Radar Conference，2014：927- 931.

［7］Zare A，Masnadi-Shirazi M A，Samadi S．Range-Doppler algorithm for processing bistatic SAR data based on the LBF in the constant-offset constellation［C］∥Proc.of the IEEE Radar Conference，2012：17- 21.

［8］Greengard L，Lee J Y．Accelerating the nonuniform fast Fourier transform［J］.Society for Industrial and Applied Mathematics Review，2004，46（3）：443- 454.

［9］Jin X X，Seok-Bum K．GPU-based parallel implementation of SAR imaging［C］∥Proc.of the International Symposium on Electronic System Design，2012：125- 129.

［10］Malanowski M，Krawczyk G，Samczynski P，et al．Real-time high-resolution SAR processor using CUDA technology［C］∥Proc.of the International Radar Symposium，2013：673- 678.

［11］Li D，Liao G S，Wang W，et al．Extended azimuth nonlinear chirp scaling algorithm for bistatic SAR processing in high-resolution highly squinted mode［J］.IEEE Geoscience and Remote Sensing Letters，2014，11（6）：1134- 1138.

［12］Chen S C，Xing M D，Yang T L，et al．A nonlinear chirp scaling algorithm for tandem bistatic SAR［C］∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium，2013：2485- 2488.

［13］Wang W，Ma Y H，Wang X P．High computation efficiency BP imaging algorithm for MIMO radar［J］.Systems Engineering and Electronics，2013，35（10）：2080- 2085．（王伟，马跃华，王咸鹏．一种高运算效率的MIMO雷达BP成像算法［J］．系统工程与电子技术，2013，35（10）：2080- 2085．）

［14］Yu M，Zhang X L，Liu Z．Acceleration of fast factorized back projection algorithm for bistatic SAR［C］∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium，2013：2493- 2496.

［15］Shi J．Researches on the principle and imaging technology of bistatic SAR and linear array SAR［D］．Chengdu：University of Electronic Science and Technology，2009．（师君．双基地SAR与线阵SAR原理及成像技术研究［D］．成都：电子科技大学，2009．）

［16］Yang H G，Yuan Y，Wu J J，et al．NUFFT applied to motion compensation in the near-space SAR imaging［C］∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium，2012：3883- 3886.

［17］Sun S L，Zhu G F．Accelerating CS radar imaging by NUFFT［C］∥Proc.of the IEEE International Conference on Signal Processing，Communication and Computing，2013：1- 4.

［18］Capozzoli A，Curcio C，Liseno A，et al．NUFFT-based SAR back projection on multiple GPUs［C］∥Proc.of the IEEE Tyrrhenian Workshop on Advances in Radar and Remote Sensing，2012：62- 68.

［19］NVIDIA C．CUFFT library［EB／OL］．［2014- 2- 13］．http：∥docs．nvidia．com／cuda／cufft／

Fast 3D imaging method for random array based on NUFFT BP

XIANG Gao，ZHANG Xiao-ling，WU Zong-liang
（School of Electronic Engineering，University of Electronic Science and Technology，Chengdu 611731，China）

Traditional two dimensional（2D）antenna array requires high pulse repetition frequency（PRF）to switch transmitters，when it is applied to 3D microwave imaging．Therefore，3D imaging is gotten by the random antenna array，as a result it reduces the requirement for PRF．Besides，a reasonable plan based on the phase center approximation（PCA）is proposed to implement the random antenna array of arbitrary geometry．The back projection（BP）algorithm interpolated by the nonuniform fast Fourier transform（NUFFT）is called NUFFT BP，and achieves high precision interpolation with relatively less computational complexity．Moreover，the NUFFT BP is further accelerated by the compute unified device architecture（CUDA）parallel computing technology，named CUDA NUFFT BP．It significantly improves the execution efficiency of the BPalgorithm．

random antenna array；nonuniform fast Fourier transform（NUFFT）；parallel computing；back projection（BP）

TN95

A

10．3969／j．issn．1001-506X．2015．04．01

向 高（1985-），男，博士研究生，主要研究方向为雷达信号处理技术、自适应信号处理、稀疏信号处理技术。E-mail：moran422＠gmail．com

1001-506X（2015）04-0725-07

2014- 05- 09；

2014- 09- 28；网络优先出版日期：2014- 11- 21。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141121．0940．010．html

国家自然科学基金（61101170）；高等学校博士学科点专项科研基金（20110185110001）资助课题

张晓玲（1964-），女，教授，博士研究生导师，博士，主要研究方向为雷达信号处理技术、分类与识别、导航定位技术。E-mail：xlzhang＠uestc．edu．cn

吴宗亮（1979-），男，博士研究生，主要研究方向为雷达信号处理技术、自适应信号处理、雷达目标识别。E-mail：nanyuanfeixue＠sina．com