基于收缩特性分析的叶丝快速对流干燥动力学模型
许冰洋,朱文魁,潘广乐,申玉军,李 斌,于川芳
中国烟草总公司郑州烟草研究院,郑州高新技术产业开发区枫杨街2号 450001
基于收缩特性分析的叶丝快速对流干燥动力学模型
许冰洋,朱文魁,潘广乐,申玉军,李 斌,于川芳*
中国烟草总公司郑州烟草研究院,郑州高新技术产业开发区枫杨街2号 450001
为准确表征叶丝脱水过程中的干燥动力学特性,分析了烤烟和白肋烟两种叶丝在下行床快速对流干燥中的孔隙结构变化特征,对叶丝干燥收缩过程进行了数学模型拟合,建立了考虑收缩形变的叶丝干燥过程水分扩散模型,并对模型进行了验证。结果表明:①随着干燥过程中两种叶丝内孔容积的减小,叶丝中孔径大于0.5μm的孔容比例呈降低趋势,而孔径小于0.05μm的孔容比例呈升高趋势;在不同干燥阶段两种叶丝孔径分布的分形维数介于2.45~2.71之间,表明其孔隙结构具有分形特征;②线性叠加式收缩模型能够较好地描述叶丝干燥过程中的收缩现象,烤烟叶丝和白肋烟叶丝体积比V/V0和含水率比X/X0的线性相关系数均大于0.99,采用该收缩模型对基于Fick第二定律的水分扩散模型进行修正,实验数据的拟合精度从修正前的0.906 9提升到修正后的0.958 0;③采用修正的水分扩散模型描述叶丝快速干燥动力学发现,考虑了干燥过程中的叶丝收缩现象后,得到的叶丝水分有效扩散系数降低,表明叶丝干燥过程中的体积收缩不利于传质过程。
叶丝;对流干燥;收缩;动力学模型
干燥脱水是烟草物料加工中的关键热湿处理环节,贯穿了烟叶原料从采后初烤、打叶复烤到制丝的整个加工流程。与已报道的果蔬、种子、木材等植物基多孔材料一致[1],片烟、叶丝等烟草物料在干燥加工过程中,由于温湿度变化引起的应力作用,均存在物理结构上的收缩形变。对于叶丝干燥过程,这一物理结构上的变化一方面可能影响最终烟支的燃烧特性[2];另一方面,由于干燥过程中水分主要通过物料内部的孔隙进行扩散和迁移[3],物理结构上的变化也会显著影响其干燥动力学。关于物理结构收缩对多孔介质干燥过程传质、传热的影响,在食品、果蔬等领域已有研究报道。Brasiello等[4]研究了收缩对茄子干燥过程中热质传递过程的影响,通过收缩系数对干燥动力学模型进行修正,能更真实地描述茄子干燥过程。Dissa等[5]以芒果片为材料,考虑了体积收缩对其干燥动力学的影响,发现材料的体积收缩不利于材料干燥过程中的传质。目前,对于烟草原料对流干燥动力学的研究,相关文献[6-8]较多采用基于Fick第二定律的扩散模型来描述烟草干燥动力学,所建立的动力学模型中均假定被干燥物料脱水过程中保持刚性,即忽略了叶丝脱水干燥过程中的体积收缩形变,也未考虑物料物理结构的变化对干燥脱水过程的影响,难以准确反映叶丝在实际脱水过程中的干燥动力学特性。基于此,在探讨两种叶丝快速对流干燥过程收缩特性的基础上,建立了考虑物料物理结构收缩的叶丝干燥动力学模型,旨在为烟草物料干燥动力学特性的分析和评价提供更为准确的模型和方法依据。
1 材料与方法
1.1 材料和仪器
以2012年河南平顶山烤烟C3F和2011年重庆白肋烟C3F为原料。片烟切丝后,在恒温恒湿间将叶丝含水率调节至30%待用。
ALPHA 1-4 LD plus型真空冷冻干燥机(德国Christ公司);DHG-9623型烘箱(上海精宏试验设备有限公司);BSA124S-CW电子天平(感量:0.000 1 g,德国Sartorius公司);UltraPYC 1200e真密度仪(美国Quantachrome公司);AutoPore IV 9500型压汞仪(美国Micromeritics公司)。
1.2 测试方法
采用郑州烟草研究院自行设计的下行床干燥试验装置进行叶丝干燥实验,装置具体结构及试验方法见文献[6]。不同干燥阶段烟丝样品含水率采用烘箱法测定[7]。将干燥后得到的叶丝样品分为两部分,一部分根据行业标准方法YC/T 473—2013[8]进行表观密度和真密度测试;另一部分经过真空冷冻干燥后,用于压汞实验以得到样品的孔径分布数据。压汞测试压力最高为414 MPa,浸润角取130°,采用仪器自带软件进行孔径分布数据处理。
2 结果与讨论
2.1 干燥过程中叶丝孔隙结构的变化特征分析
2.1.1 叶丝内孔容积的变化
叶丝属胶体毛细管多孔介质,干燥过程中极易发生收缩变形导致叶丝内部孔隙结构发生改变。如表1所示,在下行床快速干燥过程中,烤烟和白肋烟叶丝的内孔容积总体上均随含水率的降低呈减小趋势。与白肋烟叶丝相比,烤烟叶丝的毛细管收缩应力作用所导致的内孔容积减小更为显著。

表1 下行床干燥过程中叶丝内孔容积的变化
根据压汞实验结果,进一步分析了叶丝干燥过程中孔容在不同孔径区间分布的变化。对初始样品及干燥至含水率25%、15%和10%的3个不同脱水阶段的叶丝,统计分析了>20μm、0.5~20μm、0.05~0.50μm以及<0.05μm等4个孔径范围内的孔容比例,结果见图1。

图1 干燥过程中叶丝各孔径区间内对应的孔容比例
由图1可以看出:①对烤烟叶丝,干燥至含水率10%时孔径大于20μm的大孔容积比例明显降低,0.05~0.50μm的孔容比例也有所降低,而孔径小于0.5μm的细微孔容积比例则明显增加。对白肋烟叶丝,干燥过程中随着含水率的不断降低,孔径大于20μm的大孔容积比例呈先升高后降低趋势,而孔径小于0.5μm的细微孔容积比例增加明显。叶丝干燥过程中一方面由于毛细管的收缩应力使叶丝内部部分大孔及中孔孔隙会收缩成为小孔,另一方面由于叶丝含水率降低,脆性加大,叶丝内大孔及中孔孔隙出现坍塌、闭合现象,导致干燥后期烤烟叶丝和白肋烟叶丝在孔径小于0.5μm范围内的孔容比例有所增大。②与烤烟相比,白肋烟中未见孔径小于0.05μm的细微孔,说明白肋烟叶丝孔径分布范围较窄,这与前期工作[9]的分析结果是一致的。③烤烟及白肋烟叶丝孔隙中均以大孔所占孔容比例较高,干燥过程中大孔容积的变化决定了叶丝整体内孔容积的变化趋势,其中白肋烟叶丝中孔径大于20μm的大孔容积比例的变化趋势也与前期研究工作[11]中白肋烟叶丝干燥过程中内孔容积出现的阶段性上升现象相吻合。
2.1.2 叶丝孔隙结构的分形表征
为了进一步定性表征叶丝干燥过程中孔隙结构复杂程度的变化,计算了两种叶丝不同干燥阶段的分形维数。对于孔隙具有分形特征的多孔物料,孔隙结构的分形维数D一般介于2~3之间,分形维数越大表明物料孔隙表面在空间的形貌特性偏离光滑表面的程度也越远,孔隙结构复杂程度越高[10]。根据文献[11]所述方法,计算初始样品及25%、15%和10%等4个不同含水率阶段叶丝分形维数,结果见表2。由表2可知,两种叶丝的孔隙分形维数处于2~3之间,与文献[12]报道马铃薯、冻干牛肉等生物基多孔材料类似,具有明显的分形特征。对多孔介质材料,分形维数能够反映孔隙结构的复杂程度,包括材料的孔径分布、孔隙表面的粗糙度及孔隙形状规则程度等方面。根据本实验结果可知,烤烟和白肋烟两种不同材料叶丝的分形维数存在一定差异,但同种材料在干燥过程中分形维数变化不明显。这是由于干燥中材料内部的孔径分布虽然发生一定程度的变化,但与材料本身特性相关的孔隙表面的粗糙度及孔形状规则程度等因素,在干燥过程中变化不大,导致反映孔隙结构复杂度的分形维数变化并不明显。Macías-García等[13]在研究不同材料制成的活性炭的分形特征时也发现,不同材料制成的活性炭分形维数差异较大,而同种材料制成的活性炭分形维数波动范围较小,这也说明材料本身的结构特性是决定多孔介质分形维数的关键因素。

表2 叶丝孔隙结构的分形维数
2.2 叶丝干燥动力学模型分析
2.2.1 叶丝干燥收缩模型表征
干燥过程中叶丝内部在温湿度变化所引起的毛细管收缩应力等作用下,内部孔隙结构会发生改变并影响干燥过程。由于多孔介质内水分一般在孔隙内传输,叶丝干燥过程中的孔隙结构变化会导致水分在叶丝内部的迁移路径发生改变,对叶丝干燥过程中水分扩散过程产生影响。由于含湿多孔介质的体积主要由固体骨架体积和孔隙中水的体积组成,则干燥特定阶段的叶丝体积比可由式(1)确定[5]:

式中:ms—干基质量,g;ρs—叶丝干燥过程固体真密度,g/cm3;ρs0—叶丝干燥前固体真密度,g/cm3;ρw—水的密度,g/cm3;V0—叶丝初始体积,cm3;V—干燥过程中叶丝体积,cm3;X0—叶丝初始含水率,%;X—叶丝干燥过程中的含水率,%。
根据不同干燥阶段的叶丝真密度、含水率以及水的密度,由式(1)即可确定该阶段的叶丝体积比的试验值。叶丝的体积比V/V0即反映了叶丝干燥过程中的收缩程度。其中,式(1)中水的密度ρw取定值为1.000 g/cm3。表3为不同干燥阶段叶丝含水率及真密度测试结果。

表3 下行床干燥过程中叶丝含水率及真密度的变化
植物性多孔介质干燥过程中的收缩模型已有较多研究。Mayor等[14]总结了不同种类多孔介质的收缩模型,分为线性、非线性的经验模型和线性、非线性的理论模型。Vacarezza[15]在研究收缩对甜菜根干燥过程的影响时选用了薄片状的甜菜根为材料,材料的物理特征与叶丝相近,所以本实验中使用文献[16]中提出的叠加式线性理论模型,如式(2)所示,对干燥过程中叶丝的体积收缩现象进行描述:

式中:p1,p2—常数。
干燥过程中,在不同含水率阶段,两种叶丝体积比V/V0的试验结果见图2所示。同时,根据式(2)所述的线性收缩模型,在图2中对不同干燥阶段的叶丝体积比V/V0和含水率比X/X0进行了线性拟合。可以看出,两种叶丝的体积比在干燥过程中均呈下降趋势,即叶丝体积收缩程度随含水率的降低而增大。不同干燥阶段的叶丝体积比V/V0和含水率比X/X0的线性相关系数均大于0.99,表明此线性模型能够较好地描述叶丝干燥过程中的收缩现象。在下行床干燥过程中烤烟叶丝的干燥温度较白肋烟叶丝高,而烤烟叶丝的体积收缩程度仍低于白肋烟,说明叶丝本身的物性对其收缩程度影响较大。
2.2.2 叶丝水分扩散模型的修正
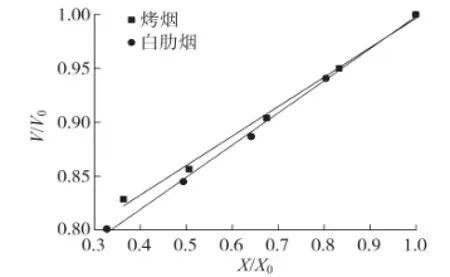
图2 叶丝体积收缩程度随含水率的变化情况
目前,对于满足薄层干燥条件的片烟、叶丝等烟草物料对流干燥过程,通常采用基于水分扩散理论的Fick第二定律来分析干燥动力学[16-17],其数学描述如式(3)所示。

式中:M—扩散介质的浓度,kg/m3;t—干燥时间,s;x—扩散距离,m;De—有效扩散系数,m2/s。
采用该理论模型对薄层干燥动力学分析过程中,普遍将被干燥物料视为刚性体,即不考虑物料的收缩形变,进而通过式(4)所示解析解[18]的形式,求解得到物料的有效扩散系数。扩散系数通常用于反映物料在一定干燥条件下的脱水能力。

式中:Xeq—平衡含水率,%;L—叶丝宽度的1/2,m;n—级数项数。
基于上述刚性物料的假设,目前在式(4)解析解方程中均将物料尺寸参数L视为常量。显然,这一假定与实际干燥过程中存在的收缩现象有较大差异。由于干燥过程中叶丝产生的体积收缩会导致叶丝内部孔隙的形态、尺寸发生改变,必然会影响干燥过程中水分的传递过程。因此,考虑叶丝体积收缩对传质过程的影响,假设水分在叶丝内的传递为一维扩散,在与叶丝切面垂直方向上进行单向传质,切丝宽度为1 mm,则L可取叶丝宽度的一半,即5×10-4m。假设干燥过程中叶丝的体积收缩为一维收缩,且收缩方向与水分传递方向保持一致,则可得到传质路径L与含水率X的关系式:

由上式可知,干燥过程中传质路径L为含水率X的函数,含水实验中干燥介质为绝干空气,相对湿度近似为零,该条件下叶丝最终的平衡含水率很小,可以忽略,则式(4)可整理为:
因此,由式(5)和(6)结合,即可在考虑物料实际收缩的条件下对烟草干燥过程中的水分变化特征进行描述,并获取相应的有效扩散系数。由实验室前期研究[16]可知,当n≥3时,有效扩散系数计算值的相对误差趋于稳定,故取n=3。
2.3 叶丝干燥动力学模型的验证
由式(6)可得到修正后叶丝干燥过程中的有效扩散系数。考虑叶丝体积收缩对传质过程的影响前后对比结果见图3。如图3所示,考虑体积收缩对叶丝干燥过程的影响并对扩散方程进行修正后,得到的理论值与实测值的相关系数从修正前的0.906 9提高到0.958 0。

图3 考虑叶丝体积收缩对传质过程的影响前后对比
叶丝体积收缩对传质过程中水分扩散系数的影响见表4。由表4可知,考虑干燥过程中叶丝体积收缩对传质过程的影响,烤烟叶丝的水分有效扩散系数由2.97×10-8m2/s降至2.12×10-8m2/s,对白肋烟叶丝,水分有效扩散系数由3.99×10-8m2/s降至2.94×10-8m2/s。可以发现,修正后叶丝的有效扩散系数明显降低,说明干燥过程中叶丝的体积收缩行为不利于传质过程,与已报道的收缩对芒果片干燥过程影响的研究结果一致[5]。

表4 叶丝体积收缩对传质过程中水分扩散系数的影响
叶丝内部孔隙结构复杂,干燥过程中水分从叶丝内部向表面扩散迁移,但并不能在任意方向上扩散,孔隙结构是决定水分传递过程的关键因素。叶丝干燥过程中发生的体积收缩现象,使内部水分传质路径在收缩方向上发生变化,但叶丝的收缩导致内部孔隙结构发生改变,使无序排列的孔隙更加复杂,内部水分在向叶丝表面迁移扩散过程中受到更多阻滞,导致叶丝内水分的有效扩散系数降低,从而也说明干燥过程中叶丝发生的体积收缩现象不利于传质过程。
3 结论
(1)干燥过程中两种叶丝的内孔容积呈降低趋势,叶丝在大于0.5μm孔径范围内的孔容比例呈降低趋势,小于0.05μm孔径范围内的孔容比例呈升高趋势,叶丝的体积收缩行为对叶丝的孔隙结构分布具有显著影响。在不同干燥阶段两种叶丝孔径分布的分形维数介于2.45~2.71之间,表明其孔隙结构具有分形特征。
(2)Vacarezza提出的线性收缩模型能够较好描述叶丝干燥过程中收缩现象,叶丝体积比V/V0和含水率比X/X0的线性相关系数均大于0.99。采用该收缩模型对基于Fick第二定律的水分扩散模型进行修正,实验数据的拟合精度从修正前的0.906 9提升到修正后的0.958 0,得到了能够更准确描述叶丝实际干燥过程的动力学模型。
(3)采用修正的水分扩散模型描述叶丝快速干燥动力学发现,考虑实际收缩条件下得到的叶丝水分有效扩散系数较未考虑收缩时低26%~28%。这也表明叶丝干燥过程中的体积收缩不利于传质过程。
[1]LIU Guohong,CHEN Junruo,LIU Meihong,etal. Shrinkage,porosity and density behaviour during convective drying of bio-porous material[J].Procedia Engineering,2012,31:634-640.
[2]李巧灵,陈晓东,李军,等.卷烟燃烧模型研究进展[J].中国烟草学报,2013,19(2):115-122.
[3]袁越锦,杨彬彬,焦阳,等.多孔介质干燥过程分形孔道网络模型与模拟:Ⅰ.模型建立[J].中国农业大学学报,2007,12(3):65-69.
[4]Brasiello A,Adiletta G,Russo P,etal.Mathematical modeling of eggplant d rying:Shrinkage effect[J]. Journal of Food Engineering,2013,114(1):99-105.
[5]Dissa A O,Desmorieux H,Bathiebo J,etal.Convective drying characteristics of Amelie mango(Mangifera indicaL.cv.‘Amelie’)w ith correction for shrinkage[J]. Journal of Food Engineering,2008,88(4):429-437.
[6]王鹏飞,刘朝贤,朱文魁,等.在气固并流下行床中烟丝的快速干燥动力学分析[J].烟草科技,2014(4):5-9.
[7]YC/T 31—1996烟草及烟草制品试样的制备和水分的测定烘箱法[S].
[8]YC/T 473—2013烟丝表观密度、真密度和内孔容积的测定[S].
[9]许冰洋,朱文魁,申玉军,等.不同干燥方式下叶丝孔隙结构的变化特征分析[J].烟草科技,2015,48(4):60-65.
[10]Mandelbrot B B.Fractals:Form,chance and dimension[M].San Francisco:Freeman,1977.
[11]ZHANG Baoquan,LI Shaofen.Determ ination of the surface fractal dimension for porous media by mercury porosimetry[J].Industrial&Engineering Chem istry Research,1995,34(4):1383-1386.
[12]刘永忠,陈三强,孙皓,等.冻干物料孔隙特性表征的分形模型与分形维数[J].农业工程学报,2004,20(6):41-45.
[13]Macías-García A,Díaz-Díez MA,Cuerda-Correa E M,etal.Study of the pore size distribution and fractal dimension of HNO3-treated activated carbons[J].Applied Surface Science,2006,252(17):5972-5975.
[14]Mayor L,Sereno A M.Modelling shrinkage during convective drying of food materials:A review[J]. Journal of Food Engineering,2004,61(3):373-386.
[15]Vacarezza L.Cinetica y mecanismo de transporte de agua durante la deshidrataci on de la remolachaazucarera[D].Buenos Aires:Universidad de Buenos Aires,1975.
[16]张合明,闫亚明,刘朝贤,等.压力对烟丝干燥有效扩散系数的影响[J].烟草科技,2011(6):5-8.
[17]刘泽,李斌,于川芳.复合传热对薄层烟丝干燥强化传质作用的动力学分析[J].烟草科技,2009(11):5-10.
[18]Crank J.The mathematics of diffusion[M].London:Oxford University Press,1975.
责任编辑 周雅宁
Kinetic Model for Rapid Convective Drying of Cut Strips Based on Shrinkage Property Analysis
XU Bingyang,ZHU Wenkui,PAN Guangle,SHEN Yujun,LI Bin,and YU Chuanfang*
Key Laboratory of Tobacco Processing Technology of CNTC,Zhengzhou Tobacco Research Institute of CNTC, Zhengzhou 450001,China
In order to accurately characterize the kinetic characteristics of cut strips inthe process of dehydration,the variation of pore structure in cut strips of flue-cured and burley tobaccos during rapid convective drying in a downflowbed was analyzed.The process o f cut tobacco drying and shrinking was fitted by a mathematic model,and the model for moisture diffusion during drying taking into account the shrinking deformation was developed and verified.The results showed that:1)W ith the decrease of pore volume of cut strips of flue-cured and burley tobaccos during drying,the proportion of volume of pores of>0.5μm in size decreased,while that of<0.05μm increased.The fractal dimension of the two tobaccos ranged from 2.45 to 2.71 at different drying stages,which indicated that their pore structure possessed fractal characteristics.2)The linear superposition model described the shrinkage of cut strips during drying pretty well,the linear correlation coefficients for the volume ratio(V/V0)and moisture content ratio(X/X0)between cut strips of the two tobaccos were higher than 0.99.The shrinkage model was used to revise the moisture diffusion model based on Fick’s second law,so that the fitting accuracy ofexperimental data increased from 0.906 9 to 0.958 0.3)From the revised moisture diffusion model,it was found that the effective diffusivity of moisture was overestimated when the shrinkage of cut strips during drying was neglected,which indicated that the shrinkage of cut strips impacted a negative influence on mass transfer p rocess during d rying.
Cut strip;Convective drying;Shrinkage;Kinetic model
TS412
A
1002-0861(2015)09-0069-06
10.16135/j.issn1002-0861.20150912
2014-11-07
2015-06-11
国家自然科学基金项目“植物多孔介质快速干燥过程微细结构变化的分形特征及对热质传递影响机制”(51306213)。
许冰洋(1990—),在读硕士研究生,研究方向:食品科学/烟草工艺。E-mail:hedaxby@163.com;*
于川芳,E-mail:yuchuanfang0208@126.com
许冰洋,朱文魁,潘广乐,等.基于收缩特性分析的叶丝快速对流干燥动力学模型[J].烟草科技,2015,48(7):69-74.
XU Bingyang,ZHU Wenkui,PAN Guangle,etal.Kinetic model for rapid convective drying of cut strips based on shrinkage property analysis[J].Tobacco Science&Technology,2015,48(9):69-74.

