例谈函数问题在数学中的意义和作用

●许钦彪 (稽山中学 浙江绍兴 312000)

例谈函数问题在数学中的意义和作用

●许钦彪 (稽山中学 浙江绍兴 312000)

函数是数学的主干知识，函数思想是数学思想的重要组成部分，函数知识、函数方法、函数应用贯穿于整个中学数学体系和教学过程，也是数学高考的重要考点.全国和各省、市每年的数学高考试题中，除了约占13%的纯函数方面试题外，还有许多其他内容的考题需要用到函数思想和方法.因而，在日常的数学教学中，必须高度重视函数及其思想、方法、技能的教学、培养和应用训练，使学生能牢固掌握、灵活应用并与其他数学知识自觉结合.

中学数学中的函数包括一次函数、二次函数、幂函数、正(反)比例函数及指(对)数函数、三角函数等初等函数.函数题型主要有函数知识应用，以及函数定义域、值域、单调性、奇偶性、周期性、对称性等性质应用，求函数解析式，求函数最值，求函数零点，函数图像应用，函数与方程、不等式、数列、解析几何等其他数学知识结合应用，含有字母参数的函数问题等.函数问题经常作为考查数学思维、逻辑推理、类比归纳、严谨运算、数形结合、分类讨论等数学能力的一种综合考查题，而且有些省、市近2年导数不作为必考要求，因此函数图像性质的应用更为重要与必要.本文就这类问题举例说明这方面的能力培养，期望同行们的参与讨论.

例1 设x1，x2为函数f(x)=ax2+(b－1)x+ 1(其中a＞0)的2个不同的零点.

1)若x1=1，且对任意x∈R，都有f(2－x)= f(2+x)，求f(x).

2)若b=2a－3，则关于x的方程f(x)=|2xa|+2是否存在负根?若存在，求出该负根的取值范围;若不存在，说明理由.

3)若 a≥2，x2－x1=2且当 x∈(x1，x2)时，g(x)=－f(x)+2(x2－x)的最大值为h(a)，求h(a)的最小值.

分析 这是一类常见的含有字母参数的二次函数问题，因为二次问题是二次函数、二次图像、二次方程、二次不等式的结合问题，涉及的知识方法较多，又在二次曲线(圆锥曲线)等其他问题上有广泛应用，所以这类问题具有典型性和代表性.

1)这是较简单的根据条件求待定字母的问题.

由条件f(2－x)=f(2+x)，得对称轴为

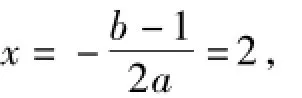
又f(1)=0，

2)这是探索性问题.要充分注意到“负根”这个条件提示，才能得到正确的解决方法.因为a＞ 0，注意到|2x－a|，若x≥，则x＞0不必考虑.所以x＜0，只需要考虑的情况.

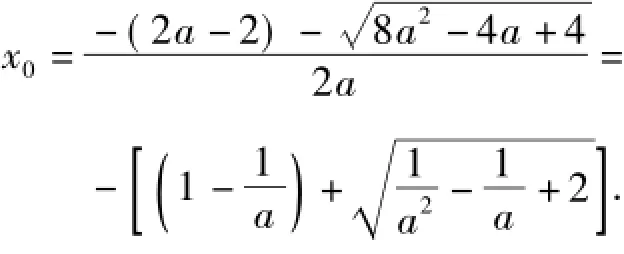
要讨论这个关于a的式子的取值范围(得用导数求最值)有一定的难度，需用单调性或图像.为了使式子变简单熟悉，可进行变量代换.

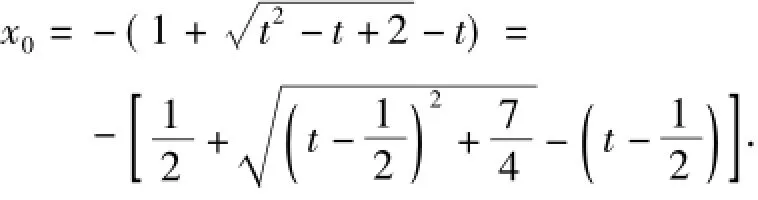
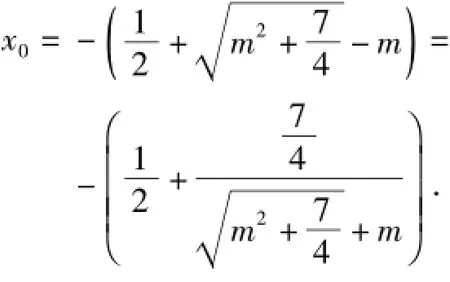
3)注意到g(x)的形式和条件x2－x1=2.

由x1，x2是f(x)的2个根，可设f(x)=a(xx1)(x－x2)，其中x1＜x＜x2，于是

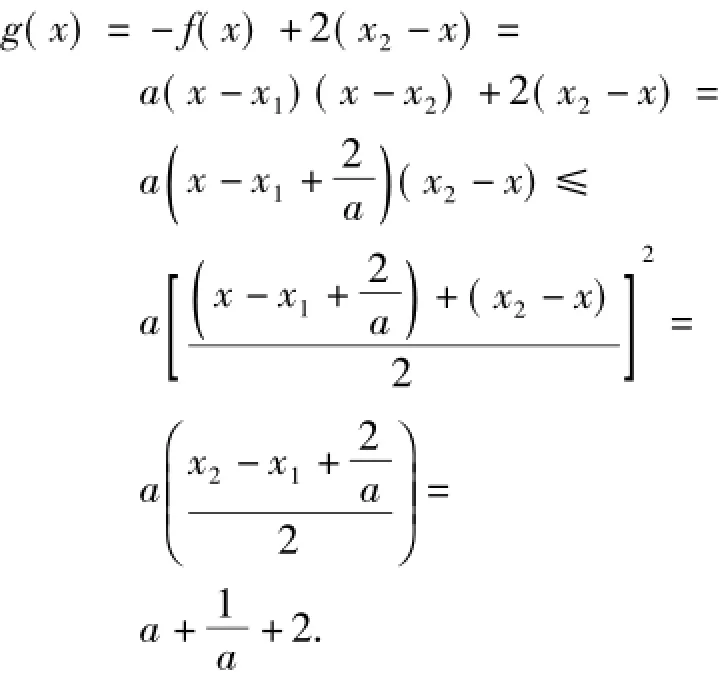
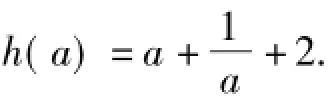
下面不利用导数证明h(a)的单调性.

设a2＞a1≥2，则于是h(a)在a≥2时是单调递增函数，从而h(a)的最小值为

点评 该题的难点在于信息量多，已知条件与所求之间关系比较难寻.在求最值和范围时，其中的式子变形、变量代换、基本不等式应用、单调性判断等均有较高的运算技能.

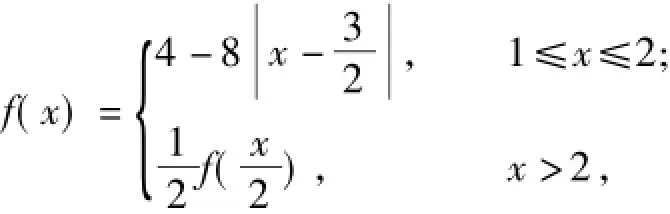
例2 定义函数求函数g(x)=xf(x)－6在区间［1，8］内的所有零点.

分析 这是一道常见的分段函数题，技巧的能力要求并不高，但需要严谨清晰的思维和计算归纳表述能力.首先，要清楚将f(x)分几段.因为当x＞2时，并不一定在［1，2］内，比如当4≤x＜6时，则

相应可得

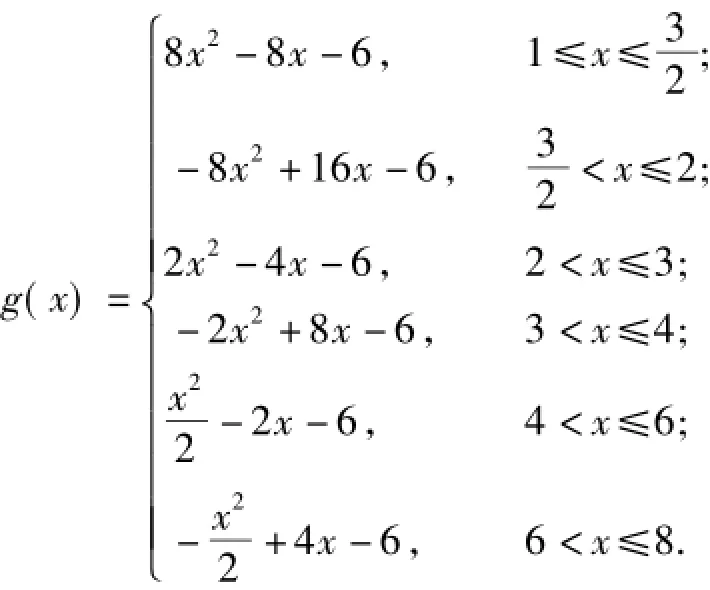
点评 该题充分体现了数学新课标中要求的“数学分析，数据处理，数学表达能力，形成锲而不舍的钻研精神和科学素质”，这也是数学思想、数学精神和数学本质的体现.这类题目有许多学生不是没有能力解决，而是没有这样的毅力意志和持之以恒的精神完整地去解决，这恰是数学精神的缺乏.建议数学教学中要有意识地利用这类问题锻炼学生的毅力.

例3 设二次函数y=f(x)=ax2+bx+c(其中a＞b＞c)，f(1)=0，且存在实数m使得f(m)=－a.

1)求证:①b≥0;②f(m+3)＞0.

2)函数y=g(x)=f(x)+bx的图像与x轴的2个交点间的距离为d，求d的取值范围.

分析 1)由f(1)=0，得a+b+c=0，

即a+c=－b.

因为 a＞b＞c，

所以 a＞0，c＜0.

又由存在实数m使得f(m)=－a，即am2+bm+ c+a=0有实根，从而

Δ=b2－4a(a+c)=b2+4ab=b(4a+b)≥0，

又4a+b=4a－c＞0，

从而 b≥0，

①得证.

从而 a＞b=－a－c，

即

2a＞－c，

得

f(m+3)＞f(1)=0，②得证.

2)由f(x)+bx=0，得ax2+2bx+c=0，

因为

Δ=4b2－4ac＞0，

所以x+x=－2b， x x=c，12a12a

从而

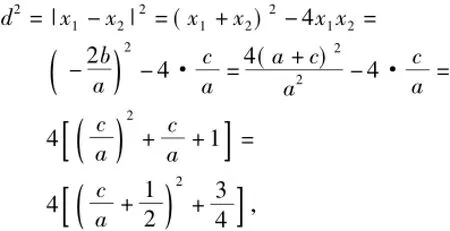
点评 要审清题意，寻求目标的具体形式和所需条件.

例4 已知a∈R，函数f(x)=x|x－a|，求f(x)在区间［1，2］上的最小值.

分析 此题目标明确，但由于含有绝对值和字母参数a，对绝对值和字母a要严谨讨论.作出函数简图，用数形结合“按图索骥”能比较清楚直观地得到解决方法.由题意可得

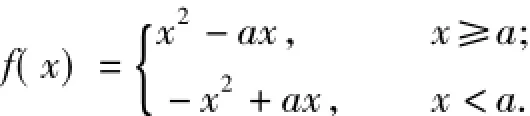
1)当a＞0时，由图1可得:

当0＜a≤1时，f(x)在区间［1，2］上递增，最小值为f(1);

当1≤a≤2时，最小值为f(a)=0;

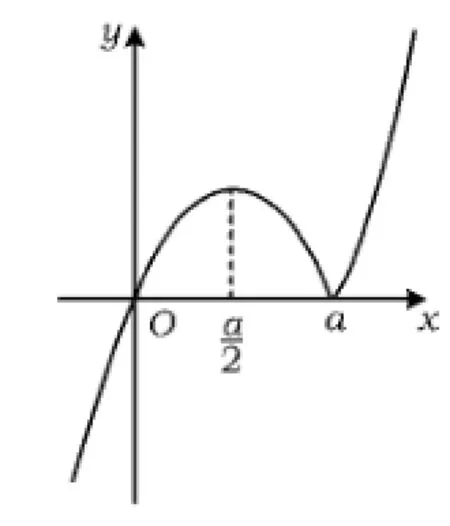
图1

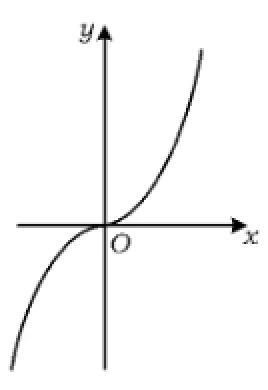
图2

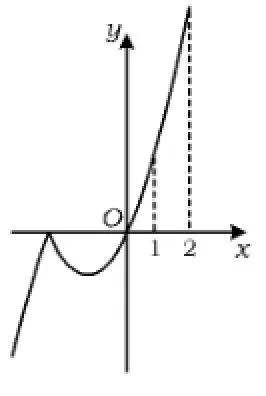
图3

2)当a=0时，如图2，最小值为f(1).

3)当a＜0时，如图3，f(x)在区间［1，2］上递增，最小值为f(1).

点评 当根据题意能作图时，数形结合、“按图索骥”、“看图说话”是一种很好的数学方法，特别对准确、快速解决探索题、讨论题有较大的作用.

例5 已知函数f(x)=|x2－1|，g(x)=x2+ ax+2，若函数h(x)=f(x)+g(x)+2在(0，2)上有2个不同的零点，求实数a的取值范围.

分析 h(x)=|x2－1|+x2+ax+4=

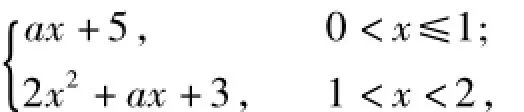
注意到h(0)=5＞0，h(1)=a+5，当1＜x＜2时是开口向上的抛物线.

讨论 1)若h(x)在(0，1］，(1，2)内各有1个根，则

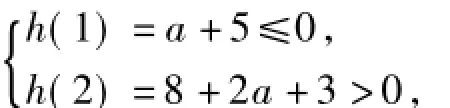
2)若h(x)在(0，1］内无根，在(1，2)内有2个根，则

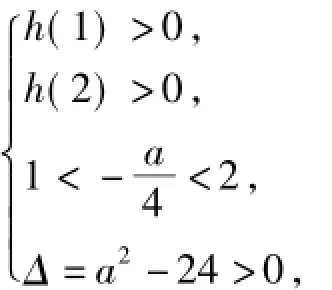
点评 这是结合函数图形从条件到结论逐步分类讨论的题型，是一类较好的数学思维训练题.这样的教学训练对学生的数学思维和解题能力有明显的效果，为解决相应的函数问题奠定了扎实的基础.如2015年浙江省数学高考文、理科试题中的函数题，许多考生就能从中受益匪浅.

例6 已知函数f(x)=x2+ax+b(其中a，b∈R)，记M(a，b)是|f(x)|在区间［－1，1］上的最大值.

1)证明:当|a|≥2时，M(a，b)≥2;

2)当a，b满足M(a，b)≤2，求|a|+|b|的最大值.

(2015年浙江省数学高考理科试题第18题)

例7 已知函数f(x)=x2+ax+b(其中a，b∈R).

2)已知函数f(x)在区间［－1，1］上存在零点，0≤b－2a≤1，求b的取值范围.

(2015年浙江省数学高考文科试题第20题)

从上可见，在函数教学中，有意识地进行函数综合问题的训练，对于培养数学思维，提升逻辑推理、合理猜想、讨论归纳、数形结合、探索创新、严谨计算等的数学品质、能力，掌握数学知识方法和提高数学方法运算技能、解题能力都是非常重要和有益的，是我们必须重视和需要充分实践的.