对一道赛题的证法探究与推广

●马占山 (五原中学 宁夏固原 756000)

对一道赛题的证法探究与推广

●马占山 (五原中学 宁夏固原 756000)

题目 设x，y，z是正实数，且xyz=1，求证:

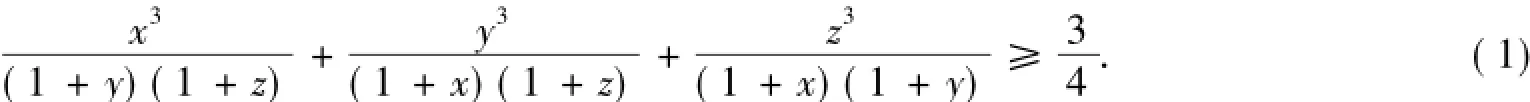
这是第39届IMO预选试题，本文主要对该赛题的解法作一些探究并进行加强和推广.

当且仅当x=y=z=1时取到等号.

证法2 不等式(1)等价于

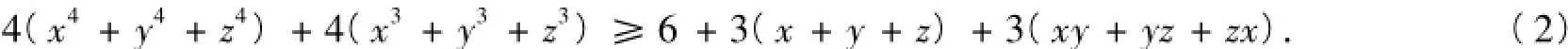
由x4+1≥2x2，可得x4≥2x2－1;又由，得x3≥3x－2，从而

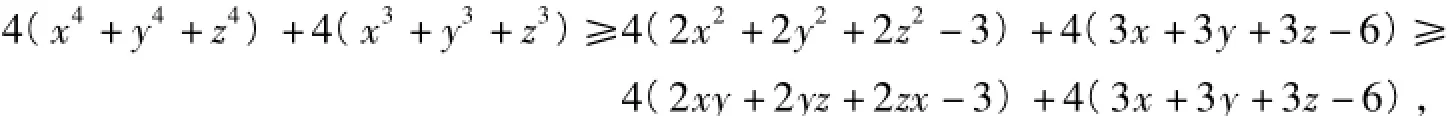
要证明不等式(2)成立，只需要证明下面不等式成立:

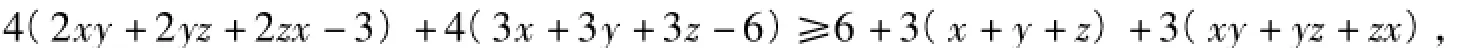
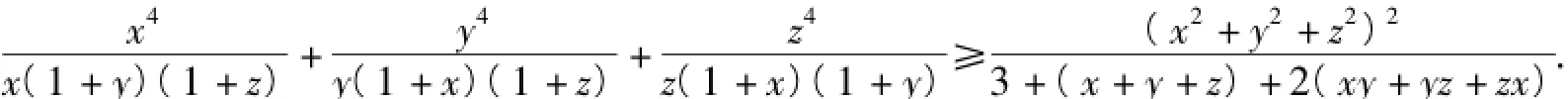
注意到

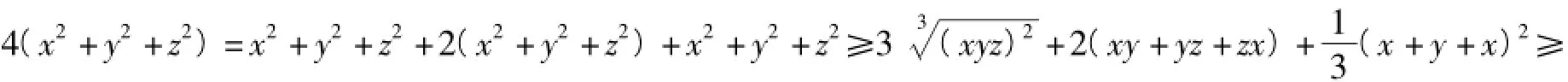
从而

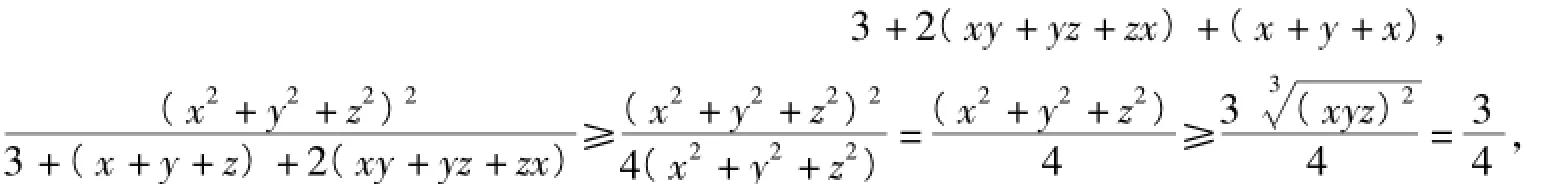
当且仅当x=y=z=1时取到等号.

对不等式(1)的左边3项x，y，z的次数进行探究得到下面2个命题:

命题1 设x，y，z是正实数，且xyz=1，则

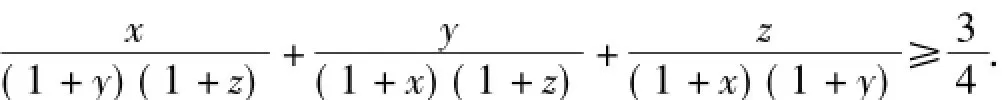
证明 该不等式等价于4(x2+y2+z2)+4(x+y+z)≥6+3(x+y+z)+3(xy+yz+zx).

注意到 4(x2+y2+z2)+4(x+y+z)≥4(xy+yz+zx)+4(x+y+z)，

因此只需证明4(xy+yz+zx)+4(x+y+z)≥6+3(x+y+z)+3(xy+yz+zx)，即

证明 该不等式等价于4(x3+y3+z3)+4(x2+y2+z2)≥6+3(x+y+z)+3(xy+yz+zx).

4(x3+y3+z3)+4(x2+y2+z2)≥4(3x+3y+3z－6)+4(xy+yz+zx)=12(x+y+z)+4(xy+yz+zx)－24，

因此，只需证明12(x+y+z)+4(xy+yz+zx)－24≥6+3(x+y+z)+3(xy+yz+zx)，即

至此，我们自然会将不等式(1)推广为

推广1 设x，y，z是正实数，且xyz=1，n是正整数，则

证明 当n=1，2，3时，前面已经证明，下面证明当n≥4时成立.此不等式等价于4(xn+1+yn+1+zn+1)+4(xn+yn+zn)≥6+3(x+y+z)+3(xy+yz+zx).

因此 xn+1+yn+1+zn+1≥x2+y2+z2.

同理可得 xn+yn+zn≥x+y+z，

于是 4(xn+1+yn+1+zn+1)+4(xn+yn+zn)≥4(x2+y2+z2)+4(x+y+z)，下面的证明过程同命题1(略).

利用证法1又可以将不等式(1)进行推广，即

证明 由三元均值不等式可得

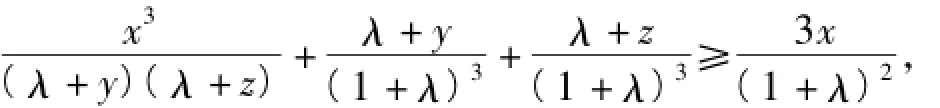
同理可得

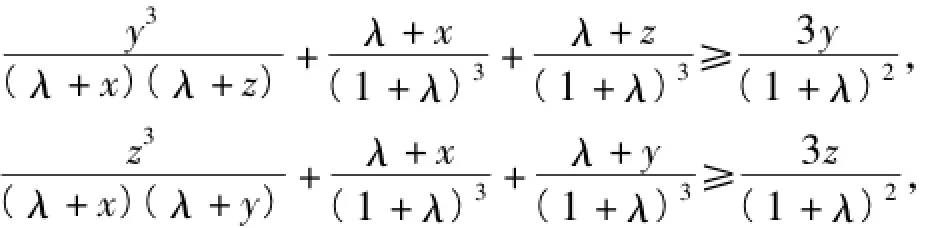
以上3个式子相加得

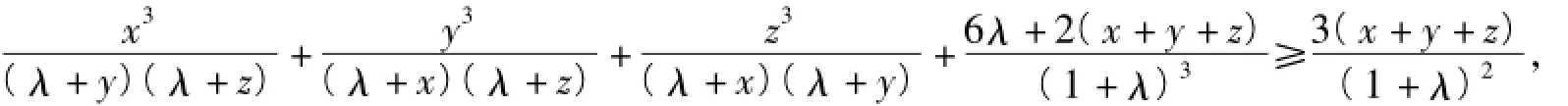
即

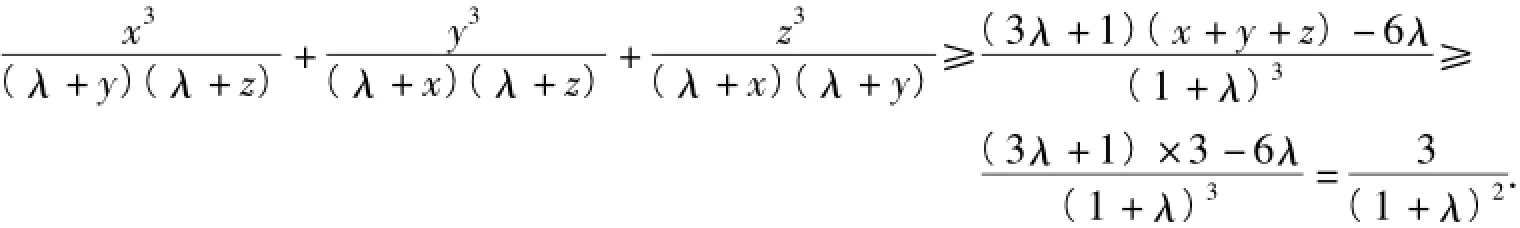
当λ=1时，即为文首的IMO预选试题.

不等式(1)可加强为

由对不等式(1)的证明过程又可得到

等价于x+y+z≥3.在条件xyz=1下，由三元均值不等式知显然成立.