关于弹簧现象的一个典型模型

布永利

【摘要】本文从多个角度对弹簧现象的一个典型问题进行了深入的研究。研究结果表明，建立物理模型和灵活地运用物理方法是很重要的。这对新课标形式下的物理教学有一定的意义。

【关键词】弹簧  加速度  位移

【中图分类号】G633.7 【文献标识码】A 【文章编号】2095-3089（2015）11-0153-01

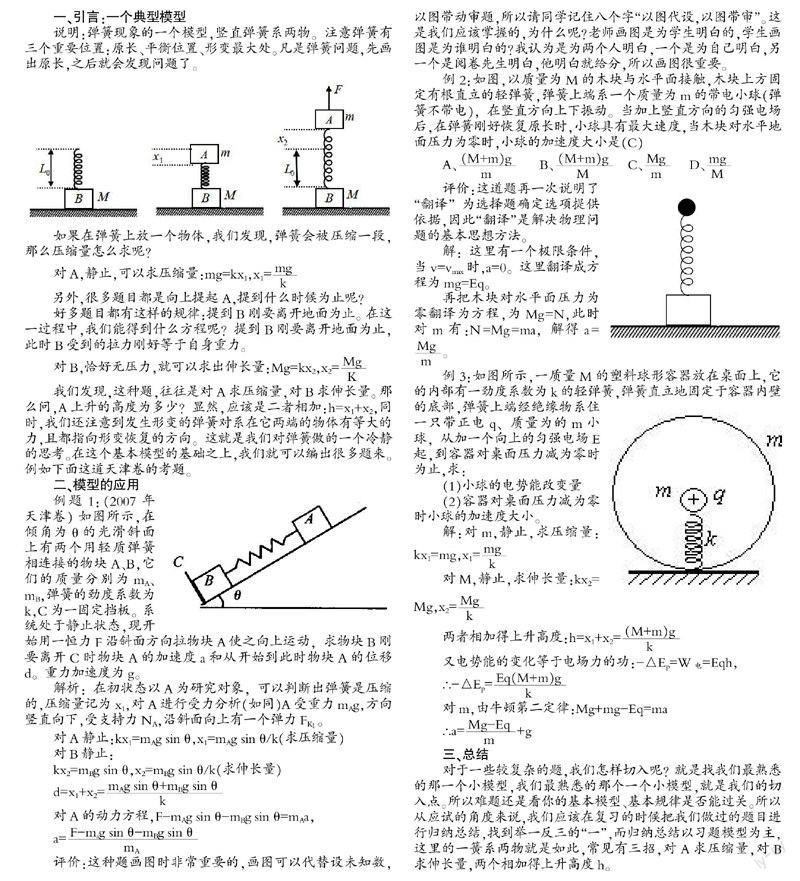
一、引言：一个典型模型

说明：弹簧现象的一个模型，竖直弹簧系两物。注意弹簧有三个重要位置：原长、平衡位置、形变最大处。凡是弹簧问题，先画出原长，之后就会发现问题了。

如果在弹簧上放一个物体，我们发现，弹簧会被压缩一段，那么压缩量怎么求呢？

对A，静止，可以求压缩量：mg=kx1，x1=

另外，很多题目都是向上提起A，提到什么时候为止呢？

好多题目都有这样的规律：提到B刚要离开地面为止。在这一过程中，我们能得到什么方程呢？提到B刚要离开地面为止，此时B受到的拉力刚好等于自身重力。

对B，恰好无压力，就可以求出伸长量：Mg=kx2，x2=

我们发现，这种题，往往是对A求压缩量，对B求伸长量。那么问，A上升的高度为多少？显然，应该是二者相加：h=x1+x2，同时，我们还注意到发生形变的弹簧对系在它两端的物体有等大的力，且都指向形变恢复的方向。这就是我们对弹簧做的一个冷静的思考。在这个基本模型的基础之上，我们就可以编出很多题来。例如下面这道天津卷的考题。

二、模型的应用

例题1：（2007年天津卷） 如图所示，在倾角为？兹的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为mA、mB，弹簧的劲度系数为k，C为一固定挡板。系统处于静止状态，现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d。重力加速度为g。

解析：在初状态以A为研究对象，可以判断出弹簧是压缩的，压缩量记为x1，对A进行受力分析（如同）A受重力mAg，方向竖直向下，受支持力NA，沿斜面向上有一个弹力FK 。

对A静止：kx1=mAg sin ？兹，x1=mAg sin ？兹/k（求压缩量）

对B静止：

kx2=mBg sin ？兹，x2=mBg sin ？兹/k（求伸长量）

d=x1+x2=

对A的动力方程，F-mAg sin ？兹-mBg sin ？兹=mAa，

a=

评价：这种题画图时非常重要的，画图可以代替设未知数，以图带动审题，所以请同学记住八个字“以图代设，以图带审”。这是我们应该掌握的，为什么呢？老师画图是为学生明白的，学生画图是为谁明白的？我认为是为两个人明白，一个是为自己明白，另一个是阅卷先生明白，他明白就给分，所以画图很重要。

例2：如图，以质量为M的木块与水平面接触，木块上方固定有根直立的轻弹簧，弹簧上端系一个质量为m的带电小球（弹簧不带电），在竖直方向上下振动。当加上竖直方向的匀强电场后，在弹簧刚好恢复原长时，小球具有最大速度，当木块对水平地面压力为零时，小球的加速度大小是（C）

A、      B、    C、     D、

评价：这道题再一次说明了“翻译”为选择题确定选项提供依据，因此“翻译”是解决物理问题的基本思想方法。

解：这里有一个极限条件，当v=vmax时，a=0。这里翻译成方程为mg=Eq。

再把木块对水平面压力为零翻译为方程，为Mg=N，此时对m有：N=Mg=ma，解得a= 。

例3：如图所示，一质量M的塑料球形容器放在桌面上，它的内部有一劲度系数为k的轻弹簧，弹簧直立地固定于容器内壁的底部，弹簧上端经绝缘物系住一只带正电q、质量为的m小球，从加一个向上的匀强电场E起，到容器对桌面压力减为零时为止，求：

（1）小球的电势能改变量

（2）容器对桌面压力减为零时小球的加速度大小。

解：对m，静止，求压缩量：kx1=mg，x1=

对M，静止，求伸长量：kx2=Mg，x2=

两者相加得上升高度：h=x1+x2=

又电势能的变化等于电场力的功：-△Ep=W电=Eqh，

∴-△Ep=

对m，由牛顿第二定律：Mg+mg-Eq=ma

∴a= +g

三、總结

对于一些较复杂的题，我们怎样切入呢？就是找我们最熟悉的那一个小模型，我们最熟悉的那个一个小模型，就是我们的切入点。所以难题还是看你的基本模型、基本规律是否能过关。所以从应试的角度来说，我们应该在复习的时候把我们做过的题目进行归纳总结，找到举一反三的“一”，而归纳总结以习题模型为主，这里的一簧系两物就是如此，常见有三招，对A求压缩量，对B求伸长量，两个相加得上升高度h。