例谈如何在课堂教学中运用《三放三收》教学

桑萍

摘要：课堂从封闭走向开放，是促使课堂“焕发生命活力”的关键环节。当教师终于克服心理上的担忧，冲破惯性思维的束缚，尝试实现“把课堂还给学生，让课堂充满生命气息”之后，一个新的问题会紧接着浮现出来：开放以后怎么办？课堂的多向、多元、多样化延伸常常会让老师感觉到无所适从。这个问题的浮现，表示着教师的教学正在经历一个重要的转型阶段。对于这个阶段的教师而言，核心的问题就是合理地处理“放”与“收”的关系，实现课堂教学“放”与“收”的和谐统一。

关键词：三放三收逐步逼近法独立思考自主性

课堂从封闭走向开放，是促使课堂“焕发生命活力”的关键环节。当教师终于克服心理上的担忧，冲破惯性思维的束缚，尝试实现“把课堂还给学生，让课堂充满生命气息”之后，一个新的问题会紧接着浮现出来：开放以后怎么办？课堂的多向、多元、多样化延伸常常会让老师感觉到无所适从。这个问题的浮现，表示着教师的教学正在经历一个重要的转型阶段。对于这个阶段的教师而言，核心的问题就是合理地处理“放”与“收”的关系，实现课堂教学“放”与“收”的和谐统一。教师设置有效合理的问题是教学的前提条件。

如在讲解《课题学习：制作一个尽可能大的无盖长方体盒子》第二课时，我原来是这样设计的：

教师先引导学生探究原正方形边长为20cm，剪去的小正方形边长h为多少时，体积最大？直至推出一般性规律：怎样才能使制成的无盖长方体盒子的容积尽可能大？教学思路是：

（1）教师直接先提出问题给学生，把剪去的小正方形边长按0.5cm的间隔取值，即分别取0.5cm，1.0cm，1.5cm，2.0cm，2.5cm，3.0cm……时，折成的无盖长方体盒子的容积将如何变化？请你制作一个统计表，表示这个变化状况。（分成8个小组，以小组为单位探索，可以使用计算器）

（2）从统计表中可以看出，当小正方形的边长取什么值时，所得的无盖长方体盒子的容积最大？此时，无盖长方体盒子的容积是多少？

（3）在得出3～4cm时面积最大，再引导学生进一步向小数探究。

我用这种方法上了一节课后，发现学生虽然是在探索，但只是沿着老师给的数据机械性的算出答案，根本就起不到让学生自己动脑思考，探究解决问题思路的目的，数学思想方法更没有学到。改变教学方法后，我决定推翻过去思路，对教学方式进行大胆的改革尝试。方法如下：

深入探究第一部分：（“一放”）

教师提问：原正方形边长为20cm，剪去的小正方形边长h为多少时，体积最大？

结论1：h=3cm时，体积最大。

教师提问：

从变化趋势上看，体积是由小变大，达到最大值再下降，你观察统计图，请问：你认为588是体积的最大值吗？你有什么想法？

“放”后生成的问题：

（1）会有同学产生质疑：剪去的小正方形的边长非得是整数吗？如果是小数，相应的无盖长方体体积是不也有可能更大?

（2）教师总结：这说明，由于刚才的方法所限，并没找到体积最大值，但能初步确定h的范围，请问：h在什么范围内，体积更大？

（3）学生得出三种结论，说明理由：2～4，2～3，3～4之间。教师让学生说，不要急于否定。总结：大家说的都有道理，h在3cm周围时（离3很近），体积更大。

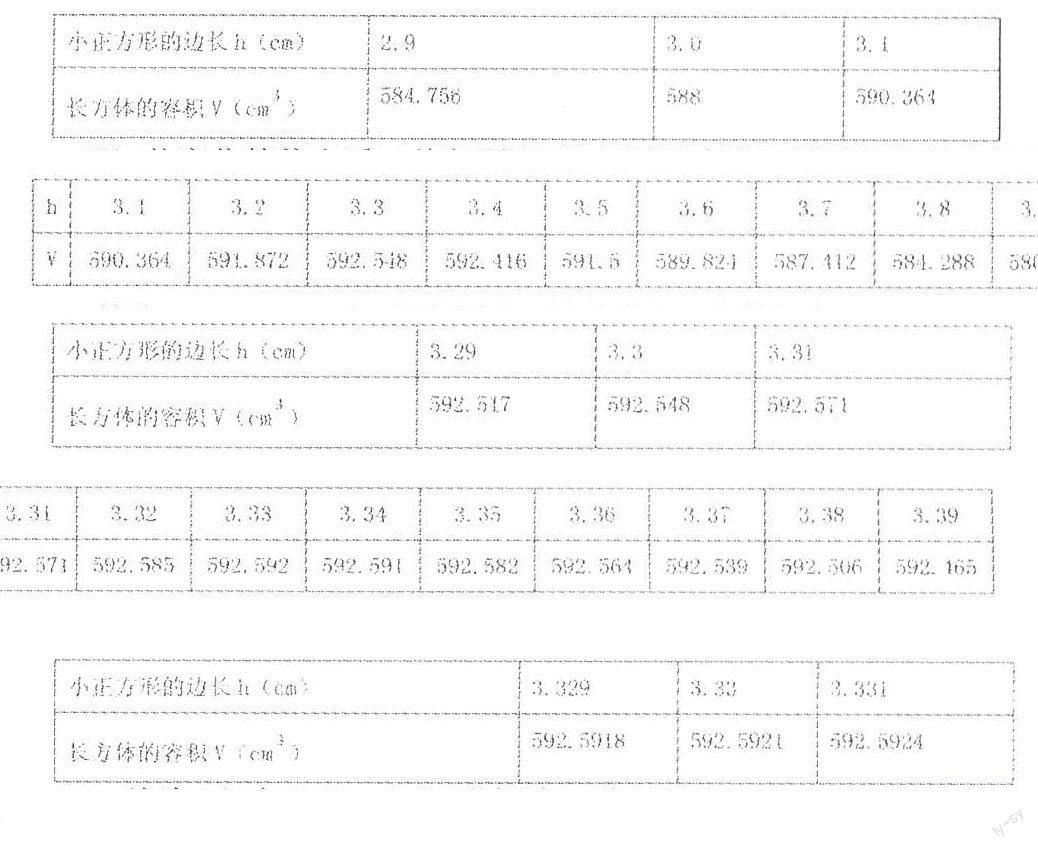
（4）2～4范围太大，但到底在哪个范围，还需要有一定的理论根据。最简单的方法，是h选择3左边的2.9和右边的3.1，分别计算出体积，看看他们的变化趋势，在进行选择，分两组计算体积，精确到小数点第三位，谁先算出就上黑板写。

（5）从变化趋势上看，体积到h=3.1时还在涨，说明体积最大值肯定就出现在3～4之间。

得出结论：h约在3～4范围内时，体积更大。

深入探究第二部分：（“二放”）

（1）接下来，我们要把这个范围进行局部放大，寻找具体h值?仿照上节课的方法，你打算怎样做?

（2）学生自然会想出：剪去的小正方形边长h按0.1cm间隔取值，找到h为多少时，体积更大。

（3）要求：每组计算一组数据，填入统计图并观察规律。

结论：h在3.33～3.34范围内，体积更大。

教师总结：

（1）这样把h的取值不断的向下细化，它将越来越接近准确值。请大家猜想下一个结果，h取多少时体积更大？

（2）最终h将逼近于哪个值?即：当正方形边长为a=20cm，剪掉小正方形边长h=3.33……3（h=10/3cm）时，体积最大。

本节课，采用三放三收的过程设计，是以大问题设计为前提，将大问题“放下去”面向全体学生开放，通过教学的重心下移，使学生的基础性资源得到生成；将学生生成的不同信息和各种资源“收上来”，为下一步形成生生和师生的互动提供互动性资源，通过生生和师生互动的方式有效利用资源，通过“收”的层次性，来实现教学过程的推进和提升。如果把问题设计十分到位，就能激发学生产生解决问题的内驱力，更能激发学生形成生层次的思考意识与习惯，这样处理巧妙的地方在于给足了学生思考和解决问题的时间和空间，更是相信了学生解决问题的潜能，提供了每个学生独立思考问题的机会。

另外，整节课都是学生思考探索方法，全班讨论可行性，然后自行分工，进行下一步的实践操作，真正体现了学生学习的自主性。用这种方法上了课之后，惊奇的发现：学生参与活动的积极性空前高涨，每个人都想迫不及待的发表自己的观点，而且对于我所教给学生的逐步逼近、细化的推理方法，学生们理解的也很透彻。因为我们的放手，本节课却获得了让人意想不到的好效果。

参考文献：

[1]孫元涛.课堂教学中的“放”与“收”[J].上海教育科研，2007，（03）.

[2]吴亚萍.数学课堂教学的“三放三收”[J].基础教育，2007，（03）.