初中数学理解性教学实验分析
黄亚
【摘要】 数学是关于数量关系与空间形式的学科,学习内容包括统计与概率、图形与几何、代数等. 数学常被理解为记忆与规则性的学科,而忽视了数学的概念性、迁移性与应用性等意义的建构. 理解是由数学本质决定的,只有在理解的基础上解决数学问题,才能实现教材之外的探究.
【关键词】 初中数学;理解性教学;实践分析
一、理解性数学教学浅析
数学理解并不是简单的记忆背诵公式,以题海战术熟知解题技巧,以便生搬硬套. 数学理解很难被认定为掌握了零散的数学法则、定理、概念、规律后,实现了解题的顺利性. 理解需要深刻认识知识体系,例如知识核心、思维方法差异、数学现象中的数学问题、数学内容间的差别等. David Perkins教授认为理解性教学不能仅注重结果,也要重视理解过程中的思维与解题方法,摆脱技能训练、知识学习的狭窄误区.
关于理解性教学国内外数学界做了许多的研究,其中大卫·铂金斯、杰伊·麦克泰、格兰特·维金斯、加德纳、琳达·达林-哈蒙德等都对理解性教学有不同的理解. 如加德纳持多元智能理论,要求课程“少即精”、分量,深入理解学科知识需要以多元智能理论为指导. 国内较为著名的有王海芬与吕林海对理解性教学所做的理论研究,陈明选所进行的“网络环境理解性教学”为以后的教学实践提供了经验.
二、进行初中数学理解性教学实验的步骤
(一)明确教学目标
理解性目标就如海上的灯塔,为前行者指明方向. 若无目标,则如无头苍蝇,到处乱窜. 在教学目标确定时,存在着抽象性,具有空泛的普适性,与现实割裂太大. 其次,教学目标应该坚持具体性,并具有激励与导向作用. 目标的确定要与各教学阶段相适应,分层设立;然后,考虑学生应该对哪些数学问题有所理解,以及何种程度的理解;目标还应该具备联系性,即此阶段目标要与学过的知识联系,如不等式、方程式与函数间的关联. 如苏科版一次函数课程,有关于“一次函数作图方法以及和图像对应关系”的教学要求. 立足于理解性教学模式,在设计目标时,应当做到:首先,函数知识囊括范围广,要求应用意识、推理能力、空间意识与符号感. 此课程以数形结合、函数与图形内容为重点目标,有必要加深理解. 其次,重视函数表达式、图像间的相互关联,并深入理解其影响程度;最后,分析一次函数以及图像与教材中所述函数及其图像间的联系,注重迁移思维. 为此,该课程目标为:函数图像的绘出,性质的描述与表达式的书写;在独立于合作学习方式下,加深理解各种函数及其图像关联.
(二)设计衍生问题
衍生问题的开放性强,要求思维以及活跃度高,是乐趣与苦恼、简单与复杂并重的问题类型. 简单在于解题主体的宽泛性,复杂在于答案理解的多层次性,答案之内又隐藏着崭新的问题. 在衍生性问题设计时,应该做到:问题选择具备启发、开放与吸引力,可得出不同答案;教材核心要囊括在问题中,以简单易懂的语言便于学生理解.
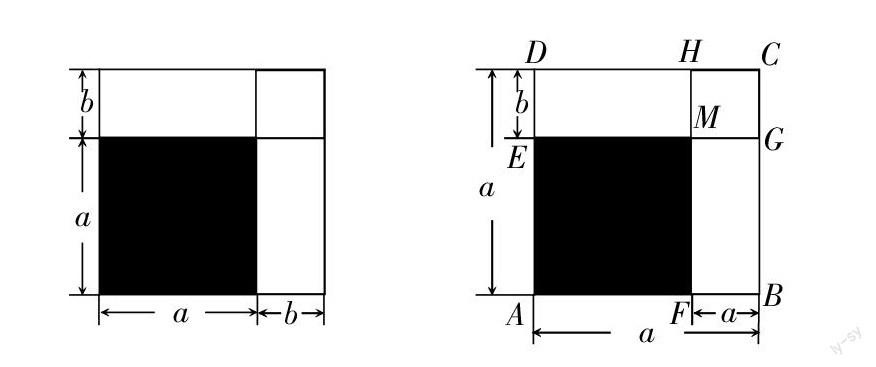
例如,关于“完全平方公式”的衍生. 此课程主要理解公式的特征,并由此得出和其余公式有何联系性,实现做题中的简化. 考虑非程序化、标准化的答案,任何学生有能力回答以及问题实践性强的要求,衍生性“完全平方公式”的设计案例为:在试验田中(正方形,边长a),为提高产量,因此进行农田扩大,得到了增加长度为b后的实验农田,实现高产目标. 总的试验田面积有多少种表达方式,对比其中的思维差异. 排除该例子,“完全平方公式”的特点还能以哪种形式体现?
(三)开展理解性活动
数学活动应该体现思维的抽象性,任何形式皆可. 如探究性学习、课题学习、研究性学习等,都是开放环境下的知识探索、理解的活动. 理解是活动的中心目标,可以通过图像、符号、语言、实物、图形等帮助学生加深理解. 理解活动设计要诀:第一,考虑学习者实际,如学习方式、学习风格与知识起点;第二,活动不可盲目追求趣味,不可忽视理解,排除华而不实,坚持有效性活动;第三,活动期间需要教师鼓励、帮助、提示.
随机与不确定现象在小学阶段学生就已经有所接触,但感受并未太深,以理解性活动——“摸球概率”为契机,便能加深理解概率概念. 教师首先准备若干袋子(不透明),并在每个袋子中装入形状相同、颜色各异的球. 指定学生以摸到某个球后停止,并问是否能摸到该色球. 在此活动,直观性、有趣性并重,学生摸球过程中猜想、疑问为何摸不着该球或第一次就摸到该球的原因,从而加深对概率知识的理解.
(四)把握理解程度
理解是思维活动,无法外显. 某些学生可能外在表现笨拙,但并不代表其洞察力缺失. 理解水平不可轻易的武断性评判,需要认真分析理解的表现、理解程度. 理解程度可通过演示、讨论、互动等方式表现出来. 教师为掌控学生是否理解,可通过活动组织、任务布置、情景创设方式进行,通过一定平台,要求学生交流、展示概念图、作品. 教师有必要做个聆听者,即使学生观点拙劣,也不排除学生的思考.
例如,以锐角三角形为例,要求学生尽量多地画出余角,并要求学生自己在本子上画出,以及挑选一名学生在黑板上演示. 学生们在不断实践中操作,观察有的学生画出了“延长线”,这时,教师就以此学生为例,向大家说明. 在理解某个问题时,教师不直接告知,而是要求主动探究,并通过实践等外在形式发现学生理解程度,以此便于针对性地提供见解,找到问题的症结点.
(五)作出理解性评价
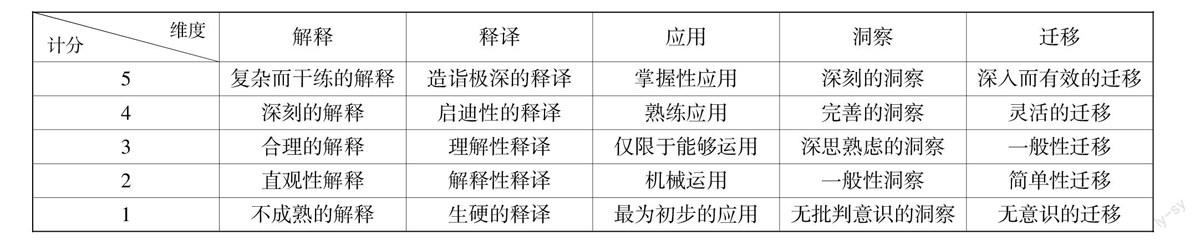
评价是总结,是掌握学生对数学问题理解程度的直观性、最后性答案. 评价应当做到:理解维度是重要的评价参考指标,如洞察、运用、解释、自我认知、移情等,具体见下表格;各维度应该有具体的评价措施与标准;结合量化与质性评价,坚持主题性、多元性原则. 在完成对各学生的理解力评分后,就要进行计分表的填写.
三、结 语
作为重要的义务教育课程,初中数学一如既往地起着抽象思维培养、逻辑推理能力锻炼的作用. 因数学形式性强,为提高学生成绩,教师往往要求学生通过记忆、题海战术取得高分,忽视理解性教学. 理解性教学是符合数学本质要求的,教师应该不断深化理论研究,吸取教学经验,为提高教学质量努力.
【参考文献】
[1]陈建华,刘金林.促进学生数学理解的线性代数教学研究与实践——以为学生提供问题解决情境为抓手[J].大学教育,2014(1):91-93.
[2]黄家深.基于实施元认知理解性数学教育作用的调查研究[J].语数外学习(数学教育),2013(6):78-78.
[3]陈家刚.促进理解性学习的课程和教学设计原则[J].全球教育展望,2013,42(1):53-61.
[4]杜娟.“数字信号处理”课程实践型教学探索[J].大学教育,2013(19):72-73.
[5]丁光辉.项目教学理论在中职数学教学中的应用研究[D].山东师范大学,2011.