线性规划在高中数学中的应用

张爱琴

简单的线性规划在现实生活中有一定的应用价值，一是改进技术，改善生产工艺；二是改进计划与生产组织，在一定条件下合理安排人力物力等资源，使经济效果达到最好.而高中数学中的线性规划问题，一般是求线性目标函数在线性约束条件下的最大值或最小值的问题，它是高中数学知识的重要内容之一，它不但能解决实际问题中的最值问题而且常在高中数学中的函数、数列、解几及向量等知识交汇处出现，具有应用的多样性，下面对平时教学中在各知识块中出现的线性规划问题进行分类和剖析，这不但能掌握一些应用线性规划解决数学中问题的方法与技巧，而且能拓展我们的数学思维.

一、线性规划在函数中的应用

例1设实数n≤6，若不等式2xm+（2-x）n-8≥0对任意x∈[-4，2]都成立，则m4-n4m3n的最小值为.

分析由题中条件可得关于m，n的不等式组，由此联想到线性规划知识求得nm的范围，再求m4-n4m3n的最小值.

图1

解设函数f（x）=2xm+（2-x）n-8=（2m-n）x+2n-8，由题意知f（-4）≥0，f（2）≥0，即4m-3n+4≤0，m≥2，n≤6.

作出关于m，n的平面可行域如图1所示.可求B72，6，C（2，6），nm表示平面区域内点与原点连线的斜率范围，又kOB=127，kOC=3，所以nm的范围为127，3.m4-n4m3n=mn-nm3，令nm=t，通过求函数g（t）=1t-t3127≤t≤3的导数可知此函数为单调递减函数，所以当t=3时函数g（t）=1t-t3的最小值为-803.

二、线性规划在解析几何中的应用

例2若方程x2a2+y2b2=1，a∈[1，5]，b∈[2，4]表示焦点在x轴上且离心率不大于32的椭圆，则z=a+b的最小值为.

分析本题是与椭圆相结合求最值的问题，由于变量a，b有二个直接条件，二个间接条件，因此此条件可以看作是关于a，b的线性约束条件.

图2

解因为离心率小于32，所以ba=a2-c2a2=1-e2≥12.由此可得1≤a≤5，2≤b≤5，ba≥12，a>b.作出可行域可得z=a+b的最小值为4.

当然在解析几何中除了在椭圆中的应用外更多的是用斜率模型和距离模型等几何意义去求最值.

三、线性规划在数列中的应用

例3等比数列{an}中的各项均为正数，若a1≥1，a2≤2，a3≥3，则a4的取值范围为.

分析根据题中的条件，由等比数列定义将条件化为关于a1与q的不等式组，由此联想到运用线性规划的知识解决问题.因此，将所得的不等式组中的每一个不等式两边都取常用对数，得到关于lga1和lgq的一次不等式组，换元：令lga1=x，lgq=y，lga4=t，得到关于x、y的二次一次不等式组，作出可行域，即可得到a4的取值范围.

图3

解设等比数列的公比为q，根据题意，得a1≥1，a1q≤2，a1q2≥3.∴各不等式的两边取常用对数，得lga1≥0，lga1+lgq≤lg2，lga1+2lgq≥lg3.令lga1=x，lgq=y，lga4=t.

将不等式组化为x≥0，x+y≤lg2，x+2y≥lg3，作出以上不等式组表示的平面区域，得到如图3的△ABC及其内部其中A（0，lg2），B（2lg2-lg3，lg3-lg2），直线l：t=x+3y经过点A时，t=3lg2取得最大值；当l经过点B时，t=-lg2+2lg3取得最小值∴t=lga4∈-lg2+2lg3，3lg2，即lga4∈lg92，lg8，由此可得a4的取值范围是92，8.

例4数列{an}为等差数列，已知首项a1>0，公差d>0，若a1+a2≤60，a2+a3≤100，则5a1+a5的最大值为.

分析由等差数列的定义将题中的不等式化为关于a1和d的不等式组，由此联想到运用线性规划知识来解决此问题.

图4

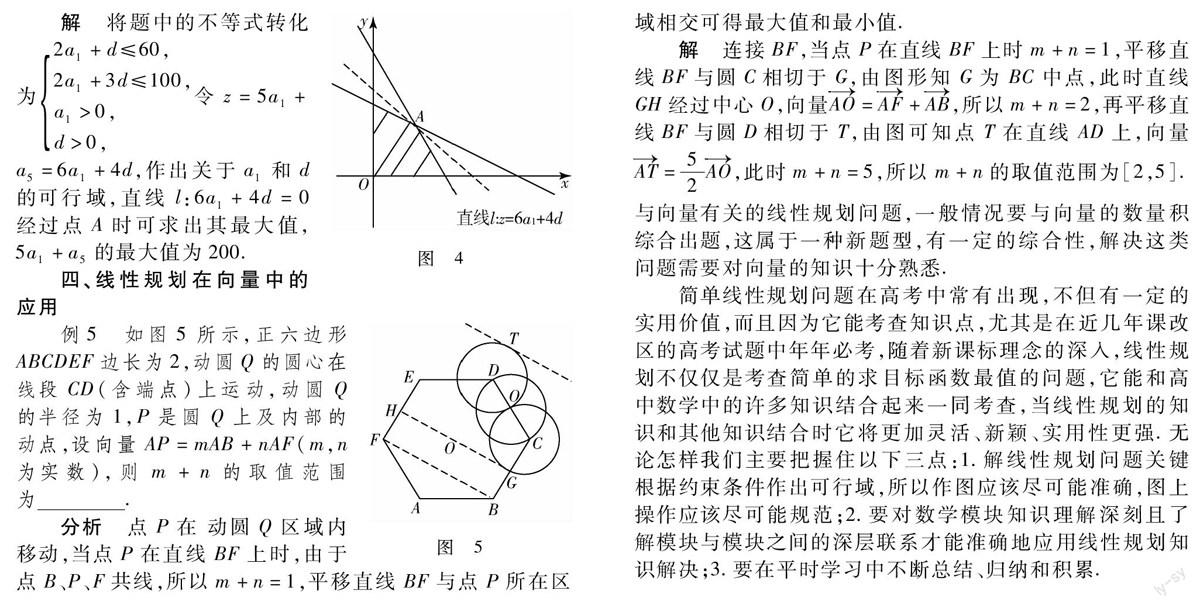
解将题中的不等式转化为2a1+d≤60，2a1+3d≤100，a1>0，d>0，令z=5a1+a5=6a1+4d，作出关于a1和d的可行域，直线l：6a1+4d=0经过点A时可求出其最大值，5a1+a5的最大值为200.

四、线性规划在向量中的应用

圖5

例5如图5所示，正六边形ABCDEF边长为2，动圆Q的圆心在线段CD（含端点）上运动，动圆Q的半径为1，P是圆Q上及内部的动点，设向量AP=mAB+nAF（m，n为实数），则m+n的取值范围为.

分析点P在动圆Q区域内移动，当点P在直线BF上时，由于点B、P、F共线，所以m+n=1，平移直线BF与点P所在区域相交可得最大值和最小值.

解连接BF，当点P在直线BF上时m+n=1，平移直线BF与圆C相切于G，由图形知G为BC中点，此时直线GH经过中心O，向量AO=AF+AB，所以m+n=2，再平移直线BF与圆D相切于T，由图可知点T在直线AD上，向量AT=52AO，此时m+n=5，所以m+n的取值范围为[2，5].

与向量有关的线性规划问题，一般情况要与向量的数量积综合出题，这属于一种新题型，有一定的综合性，解决这类问题需要对向量的知识十分熟悉.

简单线性规划问题在高考中常有出现，不但有一定的实用价值，而且因为它能考查知识点，尤其是在近几年课改区的高考试题中年年必考，随着新课标理念的深入，线性规划不仅仅是考查简单的求目标函数最值的问题，它能和高中数学中的许多知识结合起来一同考查，当线性规划的知识和其他知识结合时它将更加灵活、新颖、实用性更强.无论怎样我们主要把握住以下三点：1.解线性规划问题关键根据约束条件作出可行域，所以作图应该尽可能准确，图上操作应该尽可能规范；2.要对数学模块知识理解深刻且了解模块与模块之间的深层联系才能准确地应用线性规划知识解决；3.要在平时学习中不断总结、归纳和积累.