高中立体几何中认知策略的教学探究

郭洪莉

【摘要】本文主要探究高中生在学习立体几何时遇到思维障碍时的解题策略的教学.主要探究认知策略中综合法与分析法的应用.

【关键词】认知策略；综合法；分析法

每一科的教学中教师都重视学习方法，直到1956年，美国著名心理学家布鲁纳提出认知策略这个概念，学习方法从此被划归为认知策略的范畴.我国著名教授皮连生提出“认知策略是个人在解决思维问题时所采用的思维方式”.认知策略是个体调控内在信息加工的控制过程，一般很难外显，但是不是不能外显.本文就探究认知策略如何外显的.

数学解题中的常见认知策略：（1）顺推法：也叫由因导果法或综合法.是一种解题者由题设条件根据自己知识经验，联想、综合、概括推理导出題目结论的方法.（2）逆推法：也叫由执果索因法或分析法.是一种解题者由题目结论根据自己知识经验，联想、综合、概括推理导出题设条件的方法.（3）顺推逆推结合法：当题设条件过于复杂或繁琐时，解题者一般先用倒推根据自己知识经验，联想、综合、概括推理出题目中介结论，再结合顺推由题设条件根据自己知识经验，联想、综合、概括推理导出题目中介结论的方法.

在立体几何的课堂例题教学中，教师常常口头分析解题思路此时主要采用分析法，然后用综合法板书.用分析法时和综合法步骤类似，只是顺序不同，教学中老师往往侧重于用综合法书写，因此学生在很短时间内无法习得解题技能，解题能力比较弱.因为立体几何的问题中有许多这样的类型，题目条件很多，无法识别这些条件在解题中的先后次序，很难短时间内找到解题思路，所以学生们望而却步的居多.

下面举例说明立体几何例题教学中分析法外显的过程.

在北京师范大学出版社出版的普通高中课程标准实验教科书《数学》（必修2）中，有如下练习题：

ABCD和CDEF有一公共边CD，它们不在同一平面内，M为FC的中点，求证：AF∥平面MBD.

本题已知条件五个，①ABCD；②CDEF；③ABCD和CDEF有一公共边CD；④它们不在同一平面内；⑤M为FC的中点.对每个条件使用一般是将以前习得的知识点迁移过来然后综合使用，但是每个条件相链接的知识点都很多，如条件①ABCD，相链接的知识点分别为对边平行；对边相等；对角线相互平分，交点为对角线的中点；对角相等，还涉及内错角、同位角、同旁内角等等，本题五个条件中涉及如此庞杂的知识点，经过怎样的组合才能将此题顺利解答，因此在综合法操作起来短时间很难.

解题时审题环节中，先使用综合法分解五个条件，将每个条件链接知识在脑中做简单的汇总，即条件①ABCD和②CDEF，相链接的知识点分别为对边平行；对边相等；对角线相互平分，交点为对角线的中点；对角相等，还涉及内错角、同位角、同旁内角等等，③ABCD和CDEF有一公共边CD，相链接知识点CD与AB和EF均平行且相等；④它们不在同一平面内，相链接知识点主要是图形是立体图形，画图与看图时注意识别图形中点、线、面的层次；⑤M为FC的中点，相链接知识点主要是MF=MC，并且可能会涉及中位线.

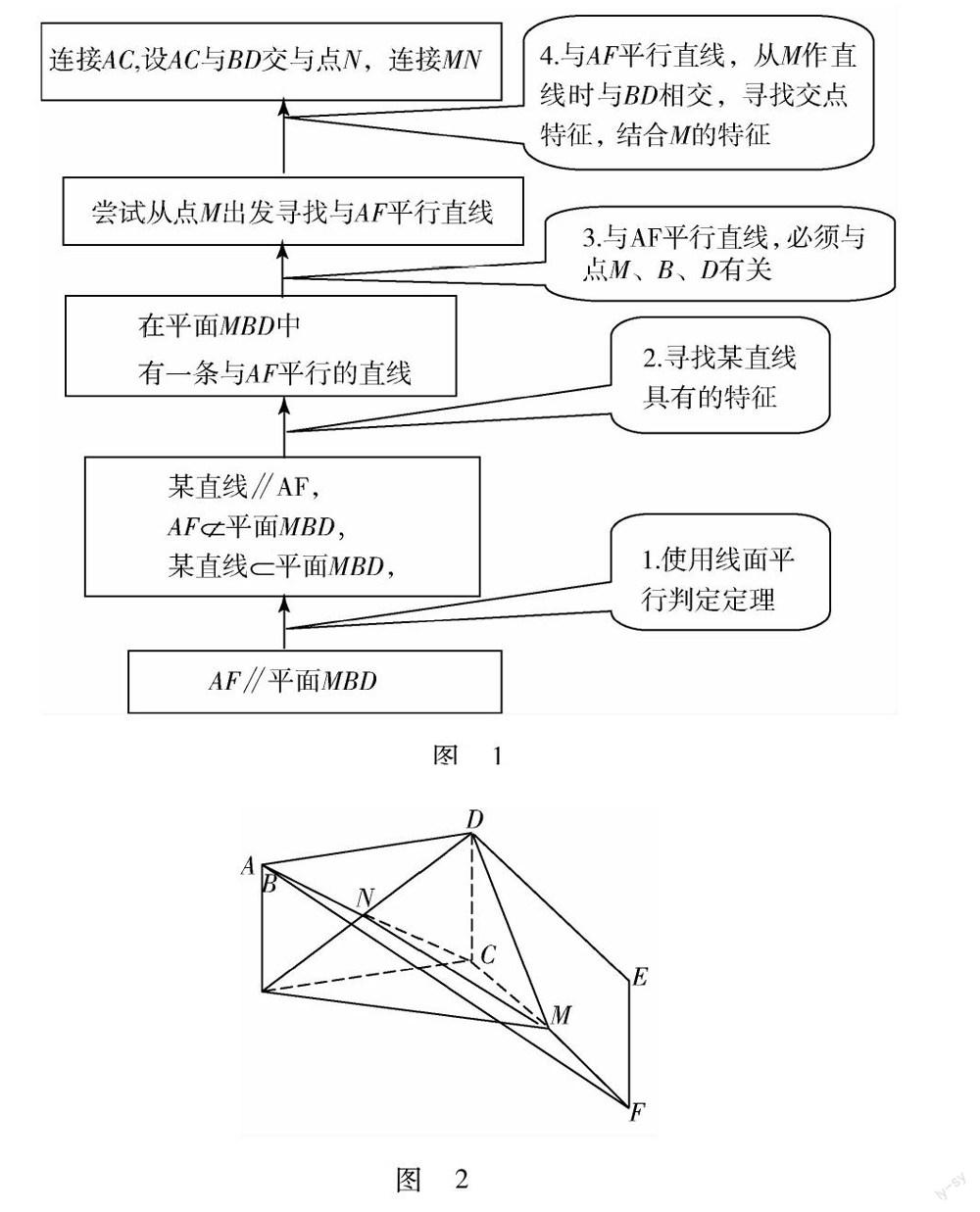
上述过程是解决用哪些知识点的思维过程.怎么解决AF∥平面MBD呢？此时采用分析法，如果综合法分析条件是发散思维过程，那么分析法恰好是集中思维过程.解法一的分析过程见图1.

图1

从图1来看，要证AF∥平面MBD，只需使用线面平行判定定理.

要用使用线面平行判定定理，只需配齐“某直线∥AF，某直线平面MBD，AF平面MBD，”这三个条件.

而已经具备AF平面MBD，只需寻找某直线具有的特征：在平面MBD中，且与AF平行；此时问题集中在“与AF平行直线，必须与点M、B、D有关”上，解决如何过M、B、D做平行与AF直线就可以了.也就是说“证明AF∥平面MBD”的问题最终转化为“过M、B、D做平行于AF直线”的问题.解法与其他方法的区别之一就是“过M做平行于AF直线”.

接下来综合法就按照从如何过M做平行于AF直线，将分析过程完全展现出来.

解法1用综合法写出解题步骤如下：

图2

证明如图2所示，连接AC，设AC与BD交与点N，连接MN.

因为四边形ABCD是平行四边形.所以点N是AC的中点，

又因为点M是FC的中点，所以点N是AC的中点.

而MN是△ACF的中位线，因此MN∥AF，

又因为AF平面MBD，MN平面MBD，

所以AF∥平面MBD.

本题还有六种解法，兹简单介绍其中两种如下：

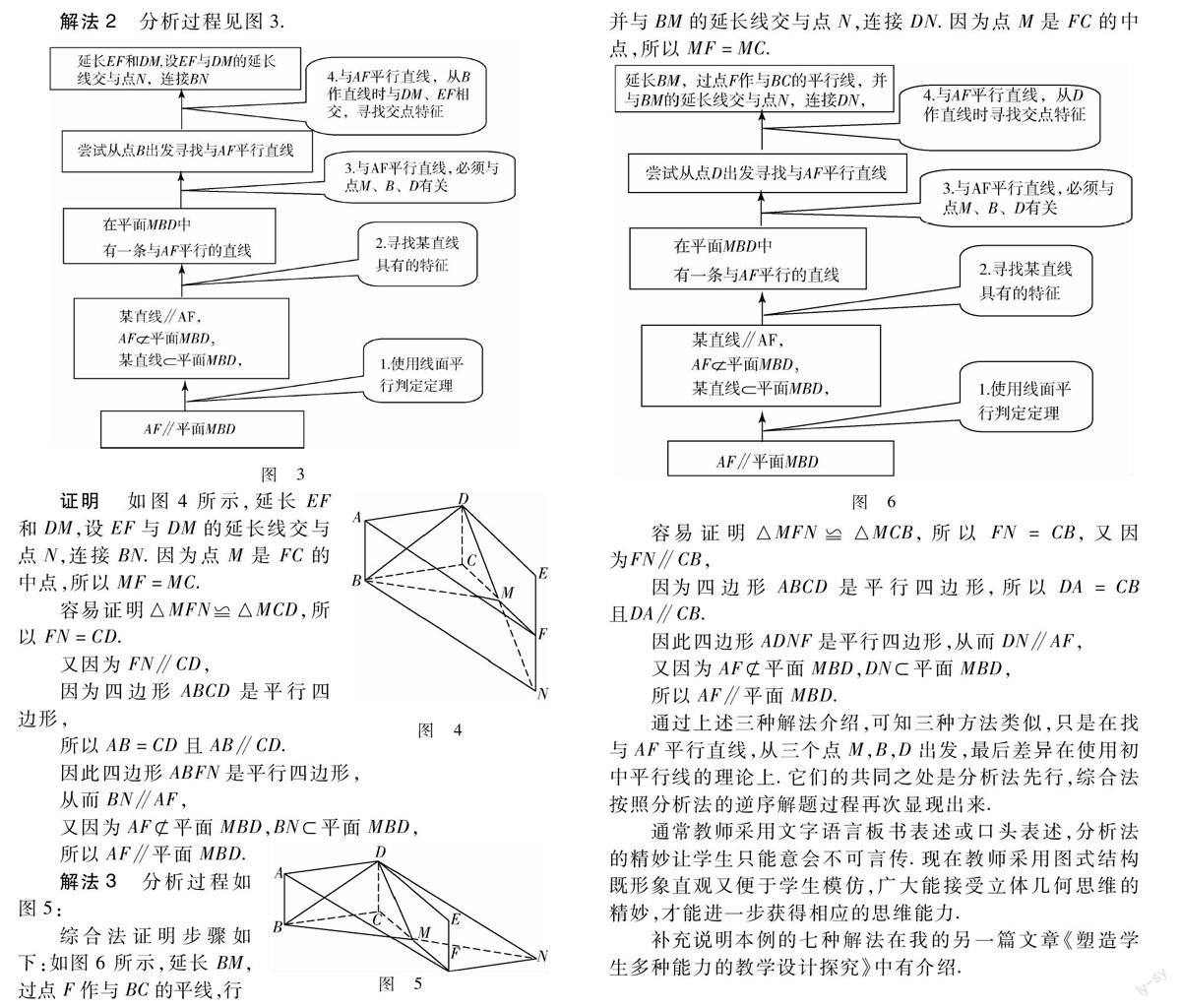
解法2分析过程见图3.

图3

图4

证明如图4所示，延长EF和DM，设EF与DM的延长线交与点N，连接BN.因为点M是FC的中点，所以MF=MC.

容易证明△MFN≌△MCD，所以FN=CD.

又因为FN∥CD，

因为四边形ABCD是平行四边形，

所以AB=CD且AB∥CD.

因此四边形ABFN是平行四边形，

从而BN∥AF，

又因为AF平面MBD，BN平面MBD，

图5所以AF∥平面MBD.

解法3分析过程如图5：

综合法证明步骤如下：如图6所示，延长BM，过点F作与BC的平线，行并与BM的延长线交与点N，连接DN.因为点M是FC的中点，所以MF=MC.

图6

容易证明△MFN≌△MCB，所以FN=CB，又因为FN∥CB，

因为四边形ABCD是平行四边形，所以DA=CB且DA∥CB.

因此四边形ADNF是平行四边形，从而DN∥AF，

又因为AF平面MBD，DN平面MBD，

所以AF∥平面MBD.

通过上述三种解法介绍，可知三种方法类似，只是在找与AF平行直线，从三个点M，B，D出发，最后差异在使用初中平行线的理论上.它们的共同之处是分析法先行，综合法按照分析法的逆序解题过程再次显现出来.

通常教师采用文字语言板书表述或口头表述，分析法的精妙让学生只能意会不可言传.现在教师采用图式结构既形象直观又便于学生模仿，广大能接受立体几何思维的精妙，才能进一步获得相应的思维能力.

补充说明本例的七种解法在我的另一篇文章《塑造学生多种能力的教学设计探究》中有介绍.