基于自主学习的初中课堂“数学活动”的设计教学探究
陈黎清
《义务教育数学课程标准(2011)》提出了“基本活动经验”的新目标,指出“学生应当有足够的时间和空间经历观察、实验、猜想、计算、推理、验证等活动过程”,明确“动手实践”也是学习数学的一种重要方式。
与此相呼应,在“课程设计思路”“课程目标”等都明确提出了“体验”、“实践”、“探究”等行为动词界定的过程性目标,因此关注学生活动性学习的教学研究也备受重视。
一、对数学活动性学习的认识
数学的活动性教学,就是让学生身历其境,直接参与、思考、再发现和再创造的学习过程。学生是过程中的主体,是实践者、研究者、探索者,而教师着重于在实践活动的基础上引导学生思考、讨论和寻找数学规律及思想,从而达到学生对数学知识的自主学习。
可以看出,数学活动性学习包括如下方面:经验的获得;概念和规律的来龙去脉;隐含在数学知识形成过程中的思想方法。
二、基于数学活动性学习的教学设计课例
数学活动性学习是指学生建立在实践活动基础上的学习。活动性学习不仅有助于完善学生已有的知识结构网络,更利于新知识在已有知识结构上的同化。实践活动不仅让新旧知识联系在一起,而且创建了一个更为丰富的、整合的知识结构。重要的是数学知识只有经过实践活动,才真正具有迁移与应用的活性,这对学生未来的发展是十分重要的。
下面我以初中“多边形内角和”(第二课时)的教学为例,通过教学过程简介及设计说明来谈谈自己在教学设计和实践中对以数学活动性学习的方式发展学生自主学习的探索与体会。
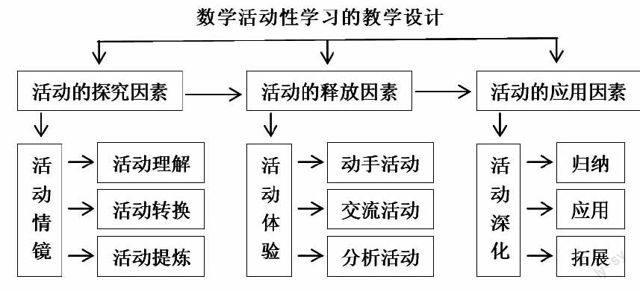
1.数学活动性学习的教学设计图
2.教学过程简介和设计意图
(1)学生活动,感知数学
活动情境:让学生用准备好的三角形纸片折叠产生出四边形,问四边形的内角和多少度?(提示:可先考虑特殊的四边形:矩形、正方形)
学生:矩形、正方形每个角都是90°,内角和为360°。
学生:猜想任意四边形的内角和可能也是360°。
教师:如何说明你的猜想是正确的呢?请每个人动手试试。
动手活动:
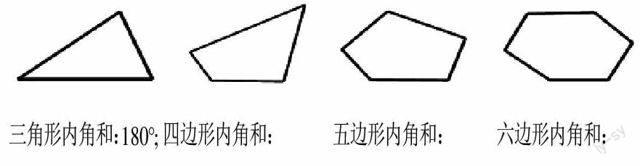
活动1:度量。用量角器量下列各多边形的内角和。
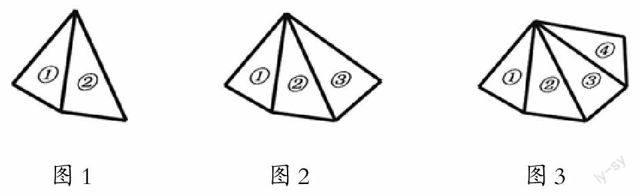
活动2:拼图。将《实验手册》(七年级下册)附录6中标有①②③④号码的四个三角形揭下,拼图
1)将标为①号、②号的三角形拼成四边形,如图1;
2)将③号三角形与图1拼成五变形,如图2;
3)将④号三角形与图2拼成六边形,如图3。
通过拼图,同学们能得到四边形、五边形、六边形内角和吗?
设计意图:通过测量活动,学生直观得到四边形、五边形、六边形的内角和,认识到多边形内角和变化的规律是边数每增加1,内角和就增加180°。拼图活动既验证了测量的正确,又让学生经历了从特殊到一般的研究过程,使学生在已有的认知结构(三角形内角和)上发展同化了新知识(多边形内角和)。这是个理解、转换、提炼的过程。
(2)自主探究,构建数学
活动情境:拼图活动中拼成的图1可以看作把四边形分割为①、②吗?
学生:可以。教师:怎么分割?学生:容易,连一条对角线即可。
由学生叙述,教师板书,附图
∠A+∠B+∠C+∠D=∠A+(∠ABD+∠DBC)+∠C+(∠ADC+∠BDC)=(∠A+∠ABD+∠ADC)+(∠C+∠DBC+∠BDC)=180°+180°
∠B分割成∠ABD与∠DBC
∠D分割成∠ADC与∠BDC
设计意图:以三角形内角和作为学生新认知的生长点,构建了学生对多边形内角和的主动探究过程。发展了学生的数学化归思维,体现出数学活动的探究因素。
活动情境:同学们记得三角形内角和是怎么集中起来化为平角的吗?四边形的四个内角如果集中起来会是什么角呢?(学生答:周角)你们有办法也把四边形的四个角集中起来拼成周角吗?
教师:先请大家画图来回忆三角形内角和是怎么拼成平角的?
学生画图:图1 图2
教师:大家能否用图1、图2类比来探索四边形内角和360°呢?
通过生生讨论、师生交流,图3、4就动态生成了。
设计意图:让学生进一步体会图形的分割、转移、合并思想。从图1图2到图3图4(DE∥AB,DF∥BC)学生又会产生类比联想。要留给学生充足的思考时间,让学生大胆发表见解,错是可以的,可以不断纠正和完善嘛,活动过程体现出了释放性因素。
(3)深化理解,应用数学
活动1:(多媒体展示)测一侧谁的推理能力强,小丽采用补图形的办法,设计了下列表格,填表:
活动2:(多媒体展示)小丽采用补图形的办法,计了如下的表格填表:
设计意图:将“多边形内角和”化归为“三角形内角和”是本节内容重要的思想方法,通过填表活动,进一步巩固了该思想,并拓展了数形结合思维,体现数学活动的应用与拓展因素。
活动情境:拿出我们用三角形纸片折叠出四边形纸片,折叠活动告诉我们大三角形(△EAB)中截去一个小三角形(△ECD)会产生四边形。那反过来如何把四边形拓展成三角形呢?
学生:可延长AD、BC交于点E,得两三角形。
教师:如何说明∠A+∠B+∠BCD+∠CDA=360°呢?(分小组讨论)
板演:∠A+∠B+∠3+∠4=∠A+∠B+(∠2+∠E)(∠1+∠E)=(∠A+∠B+∠E)+(∠1+∠2+∠E)=180°+180°=360°
设计意图:通过角的分割、转移与合并,产生求和式的拆项、交换、合并,凸显出学生探索、归纳、演绎的活动能力的提高,发散了学生思维,再次体现了数学活动的拓展因素。
三、对数学活动性学习教学设计的几点体会
1.“活动情境”是数学活动性学习的前提
课堂是师生学习活动的生态环境,创设应情应景的课堂活动情境,能让学生经历新知识发生发展的过程,会使学习过程真正成为学生在教师引导下的再发现再创造过程。可以说教师创设了符合“国情”的数学活动情境会让学生迅速适应知识的萌发和应用。
2.“活动体验”是数学活动性学习的过程
数学家Freudenthal说:数学学习如同学游泳,骑自行车,不经过亲身体验,仅仅从看书本、听讲解、观察他人的演示是学不会的。因此让学生在实践体验中获得数学知识是关键。一方面,要创设合情合理的活动情境,另一方面,要留充足的时间和空间让学生深刻体验活动,期间教师不断提供信息的链接,最大限度让学生在体验中发现新知识,在合作中主动求得能力的发展,只有如此学生才能真正体验到数学蕴含的魅力。
只有践行了实践活动的课堂,才是真正基于自主学习的课堂;只有参与了数学实践的学生,才是真正意义上的学习探究者;只有被实践了的数学,才能真正成为学生今后发展的资源。

