高斯混合模型的矩阵推广

王栋

【摘要】时间序列分析中经常出现的非高斯性质，使得传统的时间序列分析建模方法无法适用，所得到的预测值出现偏差，预测精度受到影响.本文推广了一维时间序列混合模型到多维高斯混合转移分布模型（MGMTD模型），证明了该多维时间序列混合模型下的一阶平稳性条件，并给出了该多维模型下的EM估计算法.本文将MGMTD模型应用于对我国炼焦煤炭和天然原油的价格预测分析中，实证结果显示，MGMTD模型可以得到较好的预测结果.

【关键词】混合模型；多元正态分布；MGMTD模型； EM算法；预测

1.引 言

在生产实践、科学实验与自然科学的研究中，常常需要我们去分析一系列的随时间变化的前后相互关联的观测数据，也就是我们所说的时间序列，对时间序列数据的精确处理可以使我们对未来的情况做到较好的预报和控制，对数据进行正确的建模，从而使我们发现数据中隐藏的内在规律.时间序列的例子在一些领域中是极丰富的，诸如经济、商业、工程、自然科学（特别是地球物理学和气象学）和社会科学，从Bax和Jenkins所普及的ARIMA类模型到现在，处理时间序列的问题一直是被人们所广泛研究的，在使用线性和非线性的方法上都取得了很大的发展.

在通常处理实际的时间序列问题时，为了便于计算和得到一些较好的性质，我们总是假定时间序列的误差项是服从高斯分布的白噪声，但实际情况并非如此简单，很多时间序列表现出非高斯性，例如：序列的平坦趋势、突变性、异常值点和变点等，当我们想要找到数据本身的特性对其进行预测和拟合时，根据数据所表现的特性准确建模就显得非常重要.

1996年LE等人根据Raftery（1985）的MTD模型提出了一种新的非线性时间序列模型——GMTD模型：

即给定过去的值后Yt的条件分布是混合正态分布.这个模型的特点在于它能表现出像平坦趋势、异常值、变点等实际时间序列数据常表现出来的非高斯性.并且GMTD模型的形式简单，容易处理，可以利用EM算法进行参数的估计和拟合.近年来，为了使模型具有更广泛的应用范围，很多人对这个模型做了推广，例如：2000年Wong和Li将GMTD模型推广为MAR模型，在2001年又推广为logisticMAR模型和异方差情形，Wong和Chan（2003）将模型应用到市场收益上.

混合模型是统计模式识别非常重要的方法之一，它是描述真实数据复杂性的常用方法，也是解决分类或者聚类问题的常用方法之一，在最近兴起的数据挖掘研究中也常用到它.混合模型的参数估计方法有很多，通常人们所熟知的是EM算法，在用它来做模型参数的估计时，混合的权重及成分参数是通过数据似然的局部最大化来一起估计的.

2.GMTD模型的矩阵推广

在现实世界里，很多的时间序列数据并不是仅仅用一维的模型就能够得到很好的建模，有些时候我们需要的是多维的模型.例如在股票数据里，某一只股票当前的价格可能不仅仅是和这只股票过去的价格有关，也许还同另外的其他股票的过去价格有关，为此，为了更好的对数据有更加准确的描述，我们对GMTD模型进行了推广，将它由一维的混合正态分布转化为多维的混合正态分布，即：

在时间序列分析中，序列的平稳性在模型建立和序列信息提取中具有非常重要的意义，为此我们给出多元混合转移正态分布（MGMTD）的一阶矩平稳性条件.

为了将该模型应用于实际问题的时间序列建模分析中，我们需要给出分布模型参数估计的方法.由（2）我们给出了多元混合正态的密度函数表达式，因此我们可以采用EM算法来对其进行参数估计，为此在下面内容我们推导该模型参数估计的EM算法递推公式.

首先引入潜在变量ztk，t表示第t个观测值，k表示混合模型的第k个成分，于是有：

以上两步重复进行，直到某一个特定的收敛准则满足.

在E-step通过对函数求导数并利用权重的性质∑pk=1αk=1，我们可以得到权重的估计式：

这样我们就得到了关于多元混合正态分布参数的极大似然估计的EM算法迭代表达式，可以通过该算法来计算模型中参数的估计值.

3.MGMTD模型在能源价格预测中的应用

为应对国际金融危机的影响，及时、准确反映我国主要能源产品的价格变动情况，国家统计局启动“价格调查应急机制”，对主要的能源产品进行了价格调查.由于煤炭和石油都是不可再生的重要能源资源，对其的开采和买卖对国家的发展具有重要的战略意义.为此，本文通过由国家统计局从2009年11月到2011年12月的炼焦煤炭和天然原油的半月度价格数据，数据的序列长度为50.对该二维时间序列数据进行建模，一方面研究这两种主要的能源产品的价格波动模型，另一方面希望通过数据驱动的方式研究它们之间是否存在相互的关联作用，彼此之间的价格是否存在显著的影响.对该问题的研究，将有助于对这两种重要资源的调控.

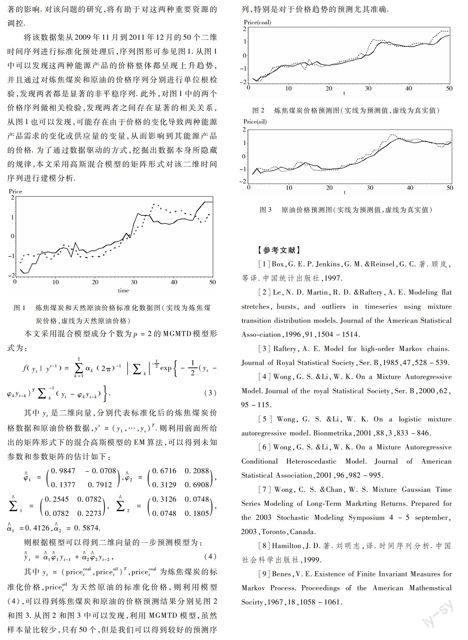
将该数据集从2009年11月到2011年12月的50个二维时间序列进行标准化预处理后，序列图形可参见图1.从图1中可以发现这两种能源产品的价格整体都呈现上升趋势，并且通过对炼焦煤炭和原油的价格序列分别进行单位根检验，发现两者都是显著的非平稳序列.此外，对图1中的两个价格序列做相关检验，发现两者之间存在显著的相关关系，从图1也可以发现，可能存在由于价格的变化导致两种能源产品需求的变化或供应量的变量，从而影响到其能源产品的价格.为了通过数据驱动的方式，挖掘出数据本身所隐藏的规律，本文采用高斯混合模型的矩阵形式对该二维时间序列进行建模分析.

【参考文献】

[1]Box，G.E.P.Jenkins，G.M.&Reinsel，G.C.著.顾岚，等译.中国统计出版社，1997.

[2]Le，N.D.Martin，R.D.&Raftery，A.E.Modeling flat stretches，bursts，and outliers in timeseries using mixture transition distribution models.Journal of the American Statistical Association，1996，91，1504-1514.

[3]Raftery，A.E.Model for highorder Markov chains.Journal of Royal Statistical Society，Ser.B，1985，47，528-539.

[4]Wong，G.S.&Li，W.K.On a Mixture Autoregressive Model.Journal of the royal Statistical Society，Ser.B，2000，62，95-115.

[5]Wong，G.S.&Li，W.K.On a logistic mixture autoregressive model.Bionmetrika，2001，88，3，833-846.

[6]Wong，G.S.&Li，W.K.On a Mixture Autoregressive Conditional Heteroscedastic Model.Journal of American Statistical Association，2001，96，982-995.

[7]Wong，C.S.&Chan，W.S.Mixture Gaussian Time Series Modeling of LongTerm Markrting Returns.Prepared for the 2003 Stochastic Modeling Symposium 4-5 september，2003，Toronto，Canada.

[8]Hamilton，J.D.著.刘明志，译.时间序列分析.中国社会科学出版社，1999.

[9]Benes，V.E.Existence of Finite Invariant Measures for Markov Process.Proceedings of the American Mathemstical Socirty，1967，18，1058-1061.