基于ARMA模型的兰州市人口短期预测研究

李姝敏　张勋尘

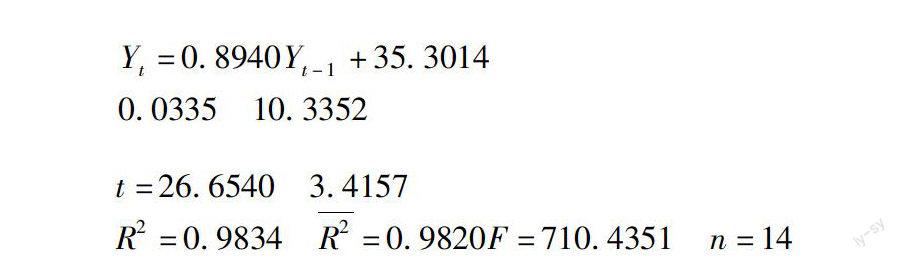
[摘 要]作为影响房价的重要因素之一，研究人口的变动规律对调控房地产行业以及国民经济运行有着重要的意义。本文以兰州市为例，选取1998—2012年年末总人口数，通过平稳性检验、阶数识别、参数检验等步骤建立ARMA模型，并对2013—2015年的预期总人口数进行估计。

[关键词]人口预测；ARMA模型；兰州市；自回归

[DOI]10.13939/j.cnki.zgsc.2015.39.054

1 引 言

近年来很多学者都对房价预测模型进行了广泛研究。李建等对我国35个大中城市同比和环比房价指数时间序列进行建模和预测，认为简单的AR模型和ARMA模型的预测精度较高[1]。侯普光等将小波分析理论和ARMA模型相结合，提出给予小波分析和ARMA模型的房价预测模型[2]。

人口总数作为我国房价主要影响因素之一，分析其变动对研究我国国民经济支柱产业之一的房地产产业的发展有着重要的指导意义。本文以兰州市为例，建立ARMA模型对短期人口总数进行预测。

2 建模预测

2.1 数据获取

本文以兰州市1998—2012年年末总人口数据为研究对象，通过建立ARMA模型对兰州市人口进行短期预测。

2.2 平稳性检测

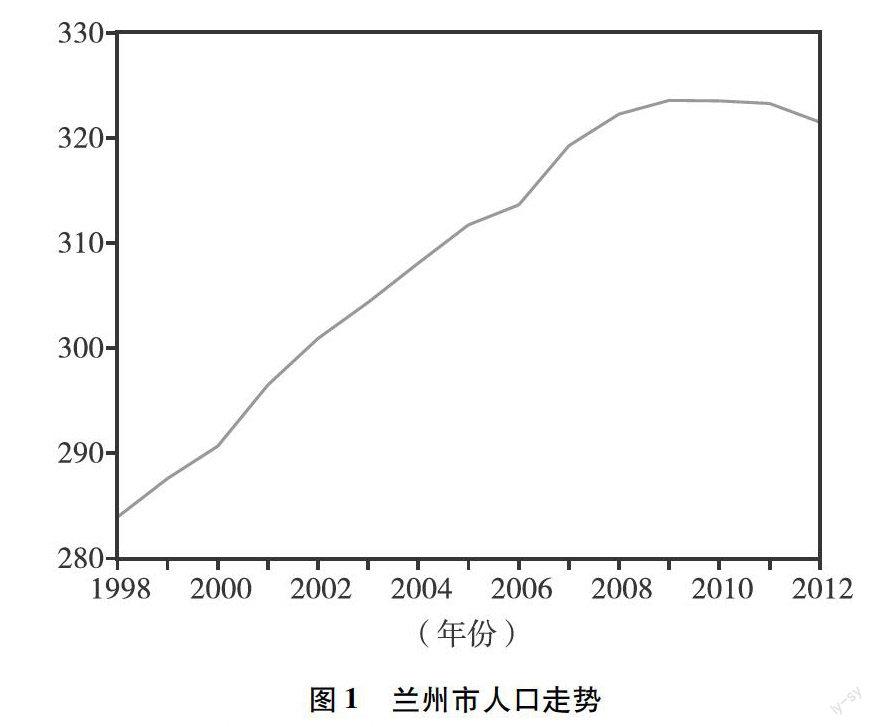
首先绘制1998—2012年兰州市人口均值走势图，如图1所示。

由图1可知，兰州市人口大致上呈上升趋势，因此需要进行相应的ADF单位根检验。Eviews 6.0检验结果如表1所示：

由ADF检验结果可知，3.1589大于3.0989和2.6904，能以5%的水平通过平稳性检验。即兰州市总人口序列在5%的显著性水平上是平稳的时间序列。

2.3 模型参数估计

ARMA（p，q）模型的识别和定阶可以依据样本的自相关系数和偏相关函数确定。将表1中的数据对数化后使用Eviews 6.0软件计算自相关系数和偏相关系数，结果如图2所示：

由图2的自相关图和偏相关图可知，时间序列自相关拖尾，偏相关截尾，选择自相关模型，p可选择1。

AR（1）模型调整后的R2为0.9820，大于AR（2）模型的0.9492；AR（1）模型的AIC值为4.0374，小于AR（2）的4.8509。因此AR（1）模型的解释程度更好。

2.4 模型检验

①显著性水平为0.05的情况下，查统计表知t检验临界值为1.782，模型两个解释变量都大于临界值，检验通过。②F统计量为710.4351，显然F检验也通过了。③模型的调整可决系数为0.9820，表明模型的拟合程度很高。

2.5 模型结果

由上一步骤的分析可知，AR（1）是最佳预测模型。模型估计结果为：

Yt=0.8940Yt-1+35.3014

0.0335 10.3352

t=26.6540 3.4157

R2=0.9834 R2[TX-]=0.9820F=710.4351 n=14

2.6 预测

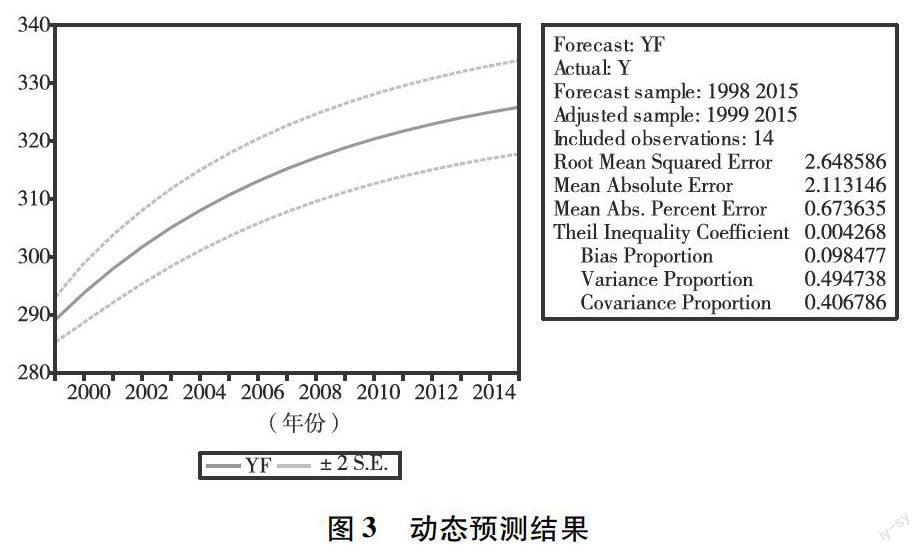
运用AR（1）模型对兰州市人口进行短期预测，预测兰州市2013年年末总人口，预测结果如图3所示：

3 结 论

本文以兰州市1998—2012年年末总人口数据通过模型识别、比较和检验，确立AR（1）模型为兰州市人口的预测模型，模型为：

Yt=0.8940Yt-1+35.3014

通过模型预测发现，ARMA模型在实际中有着广泛的适用性，可以推广到其他领域的预测。

参考文献：

[1]李建，庄健.国内35个大中城市房价指数预测[J].安徽工业大学学报（社会科学版），2014（1）.

[2]侯普光，乔泽群.基于小波分析和ARMA模型的房价预测研究[J].统计与决策，2014（15）.