培养高中生对数学图形语言的阅读能力的教学策略

蔡鹏

《普通高中数学课程标准（实验）》指出：“学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.”随着高考数学题型的变化，在选择题中出现了现学现考的题型，这就要求学生要有较高的自学能力和解决问题的能力，而阅读是自学的基础，所以要教会学生自学，就要培养学生的阅读能力，帮助学生养成良好的阅读习惯，使学生掌握一定的阅读策略.

一、什么是数学阅读、数学图形语言阅读

数学阅读是指主体在认知数学的过程中，利用不断假设、证明、想象、推理等方法，认知包含文字语言、符号语言和图形语言，同时感知和认读新概念的同化和顺应、阅读材料的理解和记忆等的积极能动的过程.

数学图形语言阅读是指学生“读”图、“画”图、“析”图、“化”图、“用”图的统称.具体包括：① 对已学的数学图形进行分析、说明；② 对新情景中的数学图形进行分析和整合；③ 对新学的数学图形的理解和记忆；④ 用原有的数学图形知识对新学的数学图形知识加以应用.

二、学生图形语言阅读现状分析

为了更好地了解中学生目前的阅读状况，我对所教的高一学生在校本课程“一元二次不等式的解法”的教学中，安排了学生自学，挑出一名同学给其他同学讲解的环节.具体情况如下：

问题1：求不等式x2 + 2x - 3 > 0的解集.

给出题目后，学生感到很吃惊，都说不会做，但是我提醒学生考虑用二次函数的图像进行求解，可是学生很迷茫，无法将图形与不等式联系起来，我认识到学生用数学图形解决数学问题的能力还很欠缺.

究其原因是多方面的，其中一个重要原因是初中教师在教学中对学生图形语言的训练不够重视，没有有效的手段训练学生图形语言的阅读，从而抑制了学生思维能力的发展，对学生后续学习也产生负面影响.

三、如何在学校教育中培养学生的数学图形语言的阅读能力

1. 明确图形语言的重要性，促使学生主动学习

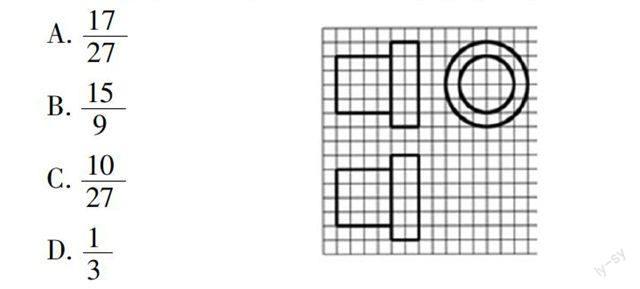
问题2：（2014·全国新课标Ⅱ）如图1，网格纸上正方形小格的边长为1（表示1 cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm，高为6 cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为 （ ）.

A. ■

B. ■

C. ■

D. ■

尽管学生、老师认为这道题是对程序框图中的循环结构的考查，其实归根结底是在考查学生对数学中的图形语言的掌握情况.在以往的高考试卷中也不乏这样的题目出现，既然图形语言的掌握是高考大纲中的要求，并且每年都出现相应的考题，这就要求每一名学生必须掌握数学图形语言的阅读，并能对其进行应用.

2. 巧设数学情境，使数学图形语言的培养成为可能

例1 求不等式 -2x - 3 > 0的解集.

解析 由 -2x - 3 > 0，得 -2x > 3，即x < -■.

所以不等式2x - 3 > 0的解集为{x|x<-■}.

探讨一元一次不等式ax + b > 0（或 < 0）的解法：（学生解决）

结论：（1）ax + b > 0的解集就是函数y = ax + b的图像落在x轴上方时的x的取值集合.

（2）ax + b < 0的解集就是函数y = ax + b的图像落在x轴下方时的x的取值集合.

例2 求不等式x2 + 2x - 3 > 0的解集.

解决方法：由例1得出的结论，让学生思考、相互讨论进行求解，然后让学生讲解过程.

探讨一元二次不等式ax2 + bx + c > 0（a > 0）的解法.（学生解决）

结论：（1）ax2 + bx + c > 0的解集就是函数y = ax2 + bx + c的图像落在x轴上方时的x的取值集合.

（2）ax2 + bx + c < 0的解集就是函数y = ax2 + bx + c的图像落在x轴下方时的x的取值集合.

3. 建立和谐的师生关系，使学生在学习数学图形语言时能大胆释疑

根据平时的观察以及与学生的交流沟通发现，不敢问问题、回答问题的学生越来越多，学生的问题意识明显下降，主要原因是“自尊心强”“回答错了怕同学嘲笑”“没有组织好自己的语言”.

现在的学生的征服欲都很强，对知识的驾驭欲望很强烈，所以作为教师，首先，要积极适应新课改的理念，做好学生的伙伴，而不是把自己的教师地位摆得很正，使学生感到畏惧；其次，学生回答问题出现错误时不要打断批评，而是欢迎其他同学补充、改进、质疑；再次，教师要鼓励学生在碰到图形、图像、图表问题时能积极思考，向老师进行挑战，充当老师的角色进行全班性的分析和讲解.

总之，教师要发挥自己的积极作用，抓好课堂教学，使学生在数学图形语言的学习上能更积极，更主动，更进一步.