浅论初中数学概念的教学方法
莫税芳
[摘要]众所周知,数学概念是数学知识的基础,只有将数学概念这一基础夯实,才能保证学生取得优异的数学成绩.基于此.从数学概念的由来、属性、形成、应用、巩固等五个方面来详细说明如何将初中数学概念教好.
[关键词]数学概念引入属性形成应用
[中图分类号]G633.6[文献标识码]A[文章编号]16746058(2015)230017
一、引入数学概念
数学概念是从现实世界中得来的,所以让学生充分理解概念的前提是给学生提供合理的物质感受,建立和准备比较好的数学概念教学模型.学生在学习和观察有关事物图案模型的同时,获得对所研究对象的感性认识,逐步认识本质,建立概念.对数学教师来讲,要开拓思维,就要多想办法动手制作一些好的数学模型,帮助学生深入理解数学概念.
二、让学生认识数学概念的属性
数学概念大都是语言性概念,要想使学生掌握好概念,必须要让学生真正认识这类概念的本质属性.例如,在给学生讲授“函数”这一概念时,可先将函数的本质特点和属性给学生讲述清楚,这样才能便于学生理解和学习.通过归纳总结的办法,将函数的属性一一逐层剖析,讲述透彻.函数的本质属性有:①“是一个变化的过程”,说明函数具有变量的属性;②“具有两个变量”,即自变量x和因变量y,说明函数是x的变化而引起y变化的一个整体关系;③“x是某一范围内确定的数值”,说明函数中x是某一范围内的数值,它具有范围性;④“因变量y值和自变量x的对应性”,说明一个x值就对应着一个确定的y值.通过上述对函数概念的逐层讲解,使学生真正认识到函数概念的本质属性就是对应关系.
三、让学生了解数学概念的形成
数学概念的教学要遵循数学概念的形成过程,并让学生了解这一过程,使学生更便于理解.给讲解学生概念的形成过程,学生能够更好地理解概念,同时能提升学生的抽象思维能力.数学本身就是着重考查学生的抽象思维能力.抽象思维能力的提高,为学生数学成绩的提高打下了良好的基础.下面我举一个简单的数学概念教学的例子.
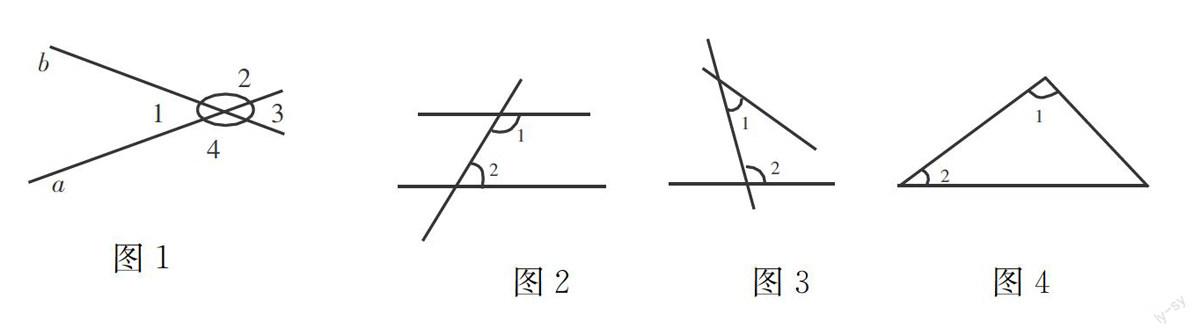
图1例如,先给学生提供图1图形,让学生分析判断这4个角的关系.因为之前学习过邻补角的概念,所以这时有学生会说:“∠1与∠2,∠2与∠3,∠3与∠4,∠1与∠4是邻补角.”不错,学生的回答没有问题.教师可以顺势再问:∠1和∠3,∠2和∠4是什么关系?这时我相信学生会说:“它们两组分别相等.”作为教师,此时就要抓住机会,在学生激烈讨论的同时,激发学生的思考意识,然后通过之前的邻补角相加之和等于180°的定理,把对顶角相等的关系给学生引出来.再利用两个木棍组成的教学模型,通过旋转木棍,使角的大小不断变化,并让学生观察发现不管角有何变化,对顶角总是相等.这样就将这一概念形象地展示给学生,使学生充分理解什么是对顶角以及对顶角的相互关系,最后引入对顶角的定义.这样,按照概念的形成过程把对顶角的概念给学生讲述了一遍,使学生更易于理解和学习.
四、让学生学会应用数学概念
掌握概念的目的就是为了更好地应用概念,只有概念在不断的应用中才能加深对概念的理解,通过对概念的应用,才能解决数学问题.例如,在给学生讲述“三角形的内切圆”这一概念后,可以给学生出一道题:如果你有一个三角形铁板,怎么利用这块三角形铁板设计出一个圆形,且这个圆形的面积是最大的.这个时候学生就会认真思考:剪出圆形并不难,但是如何才能剪出一个面积最大的圆形来呢?这时他们就会开动脑筋,想到之前学习到的数学概念,悟出:要从三角形铁板中剪出一个与三角形三边都相切的内切圆应该是最大的.这是一个一举多得、非常好的讲授数学概念的模式.
五、帮助学生数学概念
当学生获得数学概念后,必须及时地巩固,在巩固中加深对概念的理解.作为教师,我们可以通过让学生复述的方式达到巩固的目的.复述不应要求学生按照定义的具体字面意思进行复述,只要能通过自己的语言将概念的关键核心意思表达清楚即可,但重要的部分不能缺少.
以“同旁内角”的概念为例进行说明,可以为学生提供以下3种图形,让学生自己根据图形分析∠1与∠2的位置关系,这样让学生全面认识同旁内角概念,在学生在排除图3和图4的过程中,认识到图3、图4不符合,而图2符合的原因.通过这一过程使学生增强对“平行线同旁内角之和等于180°”的概念的理解.作为教师,调动学生思考的积极性是非常重要的,只有学生开动脑筋去思考去理解的时候,才能加深、巩固学生对数学概念的理解.
(责任编辑黄桂坚)

