非数学专业数学教学的简约化及高效化探究
王淑芬 王卫

摘 要:课堂教学是连接教师讲授与学生学习的重要桥梁。数学知识抽象、枯燥,学生的学习效果往往不够理想。加强数学课堂教学的简约化,可以使得学生用较少精力在较短时间内获得知识技能,并且在愉悦的过程中掌握知识,从而提高教学质量,取得事半功倍的效果。因而,在数学课堂教学过程中,提高教学的简约化和高效化就显得尤为重要。
关键词:非数学专业;数学课堂教学;简约化;高效化
上世纪90年代后期开始,我国部分高校在文科专业开设了高等数学课,2003年全国90%以上的高校文科专业都已开设了高等数学课。2000年,高等教育出版社出版了“大学生文化素质教育书系”,其中张楚廷教授著的《数学文化》指出,数学不只是关于数的世界、形的世界或更广阔的科学,数学还是一门充满人文精神的科学,“确信数学学习能够对大学生人文素质的完善起重要的作用。应当可以使大学生感到数学学习不仅不是枯燥的,数学逻辑不是冷酷的,数学亦非主要是逻辑的,应当使他们感到数学的确令人赏心悦目,能够陶冶人的情操,能够使人更聪明,而且还能够使人更高尚”。
文乃培养人的感性思维能力,理乃培养人的理性思维能力,两者缺一不可。一个仅仅懂得感性思考的人是难有建树的。数学教育不仅是专业知识的学习,更是对人的理性思维和审美意识的培养,是潜在的能动性和创造性的开发。数学这座知识殿堂美丽与严谨、神秘与枯燥同时并存。如何把精要的知识在课堂教学中有效传授给学生,把握教学过程中师生互动的准确节奏,提高数学教学的效率,达到教的轻松而学有收获的效果是我们重点探讨的。
下面针对非数学专业学生数学课程的学习进行探讨。我们这里讨论的是简约而不是简单,简约是力求言语简洁扼要,单纯明快,辞少意多。教学过程的简约化是提高课堂教学质量的有效手段。
一、数学学习重要性的简约化讲授
在数学学习的重要性上,如果第一堂课就泛泛地谈论数学的重要性,虽然本身想法是好的,很容易造成“假大空”的印象。应该针对这门课程,用适合他们专业的实例来形象地说明学习数学的重要性。
1.线性代数这门课程在水建学院的讲授
第一步:列举与所学专业相关的例子,提升学生对这门课程重要性的关注,而不是仅仅为了学分去学习一门课程。
水利工程专业的水资源管理课程中,主要应用单纯形法来求解线性方程组的最优解,进行水资源的优化配置。
[实例]某灌溉水库可控制甲、乙两灌区,其耕地面积分别为7000hm2和13000hm2,由于两地自然条件及群众种植习惯的差异,设计采用不同的综合灌溉定额及产值(表1)。
已知设年渠道最大引流量出现在七月份,该时期甲、乙两地的毛灌溉定额分别为450m3/hm2和1350m3/hm2,要求6天内灌溉全部面积。已知设计水库来水总为14500万m3,渠道及干渠設计流量为23.14m3/s,问该水库兴建后甲、乙两地灌溉面积为多少时,总产值为最高?
第二步:通过具体例子的简单分析,对所学课程有个大概印象。
分析:首先建立数学模型。设甲、乙两地灌溉面积x1,x2时,总产值为最高。约束条件有:(1)灌溉面积约束;(2)水库供水约束;(3)渠道输水能力约束。目标函数为zmax=2200x1+3000x2,然后将模型转换为标准型,用单纯型法求解(计算略)。
第三步:总结
线性代数是高等院校理工科专业的一门重要的必修基础课程。该学科具有较强的抽象性与逻辑性,概念多、符号多、运算法则多,包含的内容纵横交错,前后联系紧密,环环相扣,相互渗透。随着科学技术的飞速发展和计算机的广泛应用,线性代数所涉及的处理问题的思想、方法和技术已被广泛应用到科技的各个领域,成为各类科技人员必备的数学基础之一。
2.高等数学对信息学专业的重要性讲授设计
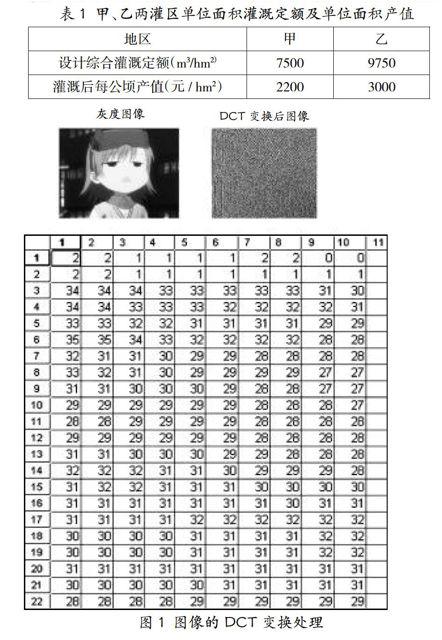
第一步:直观给学生展示三副图(图1),让学生视觉上产生冲击,加深第一印象。
第二步:对三副图及与高等数学的联系展开讲授。
数学的重要性体现在学科的各个方面,例如图象处理用到的傅立叶变换。下面三图就是现在广泛应用的图象压缩方法JPEG,采用了将图象进行DCT变换的方法。DCT变换是二维离散余弦变换,是傅立叶变换的简化。一副图象是由一个一个的象素点组成的,整个图象看作一个矩阵,矩阵的大小就是图象的分辨率,每个象素就是矩阵里的一个数字。
3.各门课程交叉融合的简约性举例
没有哪门课程是单一,可以用学或不学,有用或没用来定义。3D游戏的制作也是以图形的矩阵运算为基础的,游戏里的大量图像数据处理更离不开矩阵和高数这两个强大的工具。比如电影《阿凡达》中大量的后期电脑制作,如果没有现代的数学工具简直难以想象。
二、数学知识讲授的简约
在非专业的数学课堂上如果花大篇幅去介绍、证明太多的定理和结论,不仅让学生丧失对这门课程的学习,而且容易“未学先拒”,这样的一堂课效果肯定不理想。那么怎样将抽象、枯燥、乏味的数学知识以简约但不简单的方式传授给学生就是教师日常知识储备和提炼的最好体现。
1.高等数学中数列极限定义的简约讲授
第一步:先举数列:
(1)1,,,…,,…,
(2),,,…,,…,
(3),,,…,,…
让学生观察上述数列的特点,学生可以很容易发现数列随着下标的增大,值会越来越接近某个确定的数。此时引导学生把这个确定的数定义为常数A。
第二步:以反问的形式抛出问题,引导学生思考:怎样的量可以描述数列通项的值和确定常数接近?写出绝对值|an-A|。
第三步:描述无限接近。以数列(1)为例,an=,A=0。从具体值出发,寻找给出ε和N时机。
给定一个距离0.1,|an-A|=,<0.1,n>10,数列从第11项开始,通项与常数的距离都小于0.1.
给定一个距离0.001,|an-A|=,<0.01,n>100,数列从第101项开始,通项与常数A的距离都小于0.01.
给定一个距离0.001,|an-A|=,<0.001,n>1000,数列从第1001项开始,通项与常数A的距离都小于0.001.
……
教师让学生思考观察后,先给出结论:随着给定距离的变小,让|an-A|小于给定的距离,发现总能从某一项开始,后面的都满足通项与确定常数A的距离小于事先给定的距离。而距离的变小同时表明了通项与确定常数A的距离越来越小。此时为提出ε和N最好时机。
第四步:总结上述步骤,提炼标准抽象的极限定义:xn=a??ε>0,?正整数N,当n>N时,有|xn-a|<ε。
2.线性代数中向量线性相关与无关定义的讲述
教师在教授过程中纯粹是按照教材定义给出向量线性相关与无关的定义,学生在不能完全理解的基础上,也能固化概念,但是由此会加深数学抽象、枯燥的印象。笛卡儿说:“没有任何东西比几何图形更容易印入脑际了,因此用这种方式表达事物是非常有意义的。”如果在讲授中辅以几何图形的知识去理解抽象的概念,则会事半功倍。
第一步:数乘的几何解释为在原向量的基础上进行长度的缩放,向量加法的几何解释为依照平行四边形法则的向量合并。
第二步:线性表示的几何意义:即把向量按照平行四边形法则分解为向量组上其余向量的和。3个向量,,线性相关,画图所示(图2),可以分解为和的和。
图2 3个向量线性线性相关,,
第三步:一个向量组里,只要有一个向量可以由其他向量线性表示,我们就称这个向量组线性相关。即,,…,线性相关,不妨设被,…,线性表示,有=k2+…+kn,变形为-+k2+…+kn=,令k1=-1。
第四步:向量组,,…,线性相关,存在不全为零的数k1,k2,…,kn,使得k1+k2+…+kn=。
综上所述,通过数形结合的方式,学生对抽象的线性相关概念会有深层次的理解。高等数学、线性代数等作为高等院校各专业重要的数学基础课程,其知识已渗透到自然科学的其他各个学科,如工程技术、科学计算、经济管理等领域。如何让非数学专业的数学教育更好地发挥它应有的作用,在有限的课堂教学中提升学生学习数学的兴趣和效率,让非数学专业的数学课堂活起来、灵起来,课堂教学过程中的简约化和高效化探究就是重要的方向。提高非数学专业课堂教学的效率,使其简约化、高效化,对大学生整体数学素养的提高及专业方面创新能力的发展,无疑起着至关重要的作用。
参考文献:
[1]谢正卫,施俊.数学文化融入大学文科数学教学的意义和途径[J].江苏技术师范学院学报,2012,18(4):140-143.
[2]卢飞雁.高校文科數学教育的发展与思考[J].湛江师范学院学报,2001,22(6):96-99.
[3]张楚廷.数学文化[M].北京:高等教育出版社,2009.
[4]张卫星.简约充实:有效数学课堂本质的追寻[J].教学与管理,2008(2):29-31.
基金项目:石河子大学教育教学改革项目,项目编号:JG-2012
-166。
作者简介:王淑芬,理学硕士,石河子大学理学院讲师,主要从事数学教学工作。

