基于Matlab 的含移动副的五杆机构误差分析

冯 志，杨 光，许志乐，李 娜

(武汉理工大学 机电工程学院，湖北 武汉430070)

平行四边形刀架机构可以实现曲轴连杆颈的随动车削［1］，但其存在如下不足之处。①平行四边形机构具有一个自由度，因此需要一个原动件，那么当平行四边形机构的四杆处在一条直线上时，从动件的运动方向不确定［2］;②平行四边形机构由旋转副联接而成，由于旋转副间隙的存在，刀架连杆将沿水平方向“蹿动”，从而导致“扎刀”现象［3］。通过对平行四边形机构的变形可以弥补上述不足，并分析新机构中各杆件的杆长精度对机构位置的影响。

1 含移动副的五杆机构

为解决平行四边形机构的不足，在平行四边形机构基础上演化出含一个移动副的五杆机构，该机构是由移动副和旋转副联接而成的五杆机构［4］，如图1 所示，滑块4 长度为无限长时，D的轨迹变为直线，而D处的旋转副变为移动副。

由于带移动副的五杆机构运动副的刚度与杆长精度是相互独立的，不存在耦合问题［5］，因此，暂不考虑连接副的精度问题，独立地分析各个杆件的杆长精度对连架杆2 上尖点M点位置误差的影响。

2 误差分析理论

实际工程的机构中均会存在测量误差、加工制造误差及装配误差等，而机构在运动过程中，由于各种阻力的存在亦会产生一定的变形。以上静态与动态因素综合改变着机构的实际运动轨迹，使得实际机构与理想机构之间存在差别，该差别即为机构误差［6］。从动件的位置参数φk可由机构的相关参数表示，其表达式为：

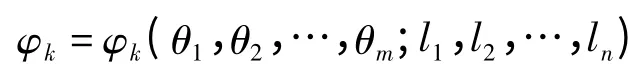
可简写为：

式中：m为机构自由度;ln为构件尺寸参数;φk为从动件k的位置参数;θi为第i个广义坐标;lj为第j个尺寸参数值;Xr(r=1，2，…，n)为(θi，lj)的缩写。

由于加工制造、装配等影响因素，实际机构中不可避免存在误差，当从动件存在误差ΔXr时，上式可变形为：

图1 五杆机构模型

假定误差ΔXr相互独立，因此将式(1)在X=Xr处按照泰勒级数展开，由于ΔXr对于Xr来说是很小的，因此二阶及以上阶数的微分部分忽略不计，展开后可得：

式中：φk为从动件k的实际位置;φk(Xr)为从动件k的理想位置，从而得到从动件k的位置误差为：

3 误差计算与分析

3.1 误差计算

含一个移动副的五杆机构的自由度为2，因此需要两个主动件即连架杆1 和连架杆3 为主动件。这里需要两连架杆的初始相位和转速都相同，可以利用差速轮系做到这点，类似于最基本的同向等角速平面铰链四杆机构［8］，即θ1=θ3。由于只考虑杆长精度误差对机构中尖点M的位置误差的影响，因此，θ1=θ3且为准确值。L为BM长度值，L1为AB长度值，L2为BC长度值，L3为CD长度值。计算过程如下：

由图1 可知，坐标原点A到连杆上点M(xM，yM)的向量为：

将式(4)写成分量形式：

根据微分定理可知，dxM≈ΔxM;dyM≈ΔyM;dLi≈ΔLi;dθi≈Δθi。将式(5)两边微分并结合微分定理，可得：

根据四边形ABCD的矢量封闭，可得：

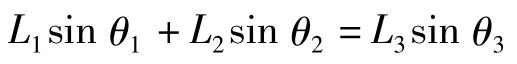
可变形为：)

在此需要四边形ABCD为平行四边形，故θ2为微量，即sin θ2≈θ2，cos θ2≈1，因此，式(7)可变形为：

将式(8)两边微分，可得：

将式(9)代入式(6)中，即可得到机构M点处的位置误差。根据式(5)可知，在理想的情况下，θ2应为零，进而尖点M的理想位置为以点(-L，0)为圆心，以L1为半径的圆。综上，在只考虑杆长精度影响的情况下，相对于连架杆1 和连架杆2 的杆长精度而言，连架杆3 的杆长精度对尖点M的位置误差影响更小。在式(6)中，因为θ1为准确值，所以可以判断连架杆1 的加工精度对连架杆2 上M点的位置误差影响最大。

3.2 Matlab 仿真计算分析

笔者分4 种情况进行仿真计算。

(1)各杆件加工精度全部取7 级精度，尺寸为：L1= 60.5 ± 0.015，ΔL1= 0.03;L2= 600 ±0.035，ΔL2=0.07;L3=60 ±0.015，ΔL3=0.03;L=250±0.025，ΔL=0.05，计算结果如图2 所示。

图2 各杆件为7 级精度计算结果

图2 结果显示，尖点M水平方向的位置误差在-0.08 ～-0.02 之间波动，而垂直方向的位置误差在-0.03 ～0.03 之间波动。

(2)杆件1 取8 级精度，其余取7 级精度，尺寸为：L1=60.5 ±0.023，ΔL1=0.047;其余尺寸与情况(1)相同，计算结果如图3 所示。图3 显示，尖点M的水平方向的位置误差约在-0.10 ～0 之间波动，而垂直方向的位置误差约在-0.045 ～0.045之间波动。

(3)杆件2 取8 级精度，其余取7 级精度，尺寸为：L2=600 ±0.11，ΔL2=0.22;其余尺寸与情况(1)相同，计算结果如图4 所示，结果与情况(1)接近。

图3 杆1 为8 级精度计算结果

图4 杆2 为8 级精度计算结果

(4)BM段的杆长L取8 级精度，其余取7 级精度，尺寸为：L=250 ±0.04 ，ΔL=0.08，其余尺寸与情况(1)相同，计算结果如图5 所示。

图5 BM 段8 级精度计算结果

图5 结果显示，尖点M的水平方向的位置误差约在-0.11 ～-0.05 之间波动，而垂直方向的位置误差约在-0.03 ～0.03 之间波动。

比较图2 与图3 可知，连架杆1 的杆长精度降一个等级，即变为8 级时，尖点M的水平方向的位置误差由-0.08 ～-0.02 之间波动变为约在-0.10 ～0 之间波动，而尖点M的垂直方向的位置误差由-0.03 ～0.03 之间波动变为约在-0.045 ～0.045 之间波动。由此可见，连架杆1的杆长精度对尖点M的位置误差影响很大。

比较图2 与图4 可知，连架杆2 的杆长精度降一个等级，即变为8 级时，尖点M的水平方向和垂直方向的位置误差均与连架杆2 的杆长精度为7 级时的位置误差很接近，因此，适当降低连架杆2 的杆长精度对误差影响不大。连架杆3 的杆长精度对尖点M的位置误差的影响比连架杆2的杆长精度对尖点M的位置误差的影响更小。

比较图2 与图5 可知，BM段杆长L的精度降为8 级时，尖点M的水平方向的位置误差由-0.08 ～-0.02 之间波动变为约在-0.11 ～-0.05 之间波动，而尖点M的垂直方向的位置误差依然约在-0.03 ～0.03 之间波动，可以看出，BM段杆长L的杆长精度对尖点M的水平方向的位置误差影响较大。

4 结论

构建机构位置方程组后，利用全微分法对其求全微分可以直接得到机构位置误差方程组［9］，因此利用全微分法对含有一个移动副的五杆机构的杆长误差导致的机构误差进行计算，而借助Matlab 软件强大的数据处理能力［10］，将尖点M的位置误差随着曲柄变化显示出来，即连架杆1的旋转而变化的具体数据可视化，有助于更加科学地分析出两者之间的关系，为以后的工作提供科学的指导。

［1］杨光，王三武，黄继雄，等.曲轴外圆切削加工方法：中国，CN200810046773.8［P］.2008 -07 -16.

［2］孙恒，陈作模.机械原理［M］.北京：高等教育出版社，2000：100 -134.

［3］李辉鹏，杨光，薛利峰，等.实现曲轴随动车削的刀架机构分析［J］. 武汉理工大学学报，2012，34(5)：127 -128.

［4］卢迪.可调曲柄长度圆度平动刀架的研究及精度分析［D］.武汉：武汉理工大学图书馆，2013.

［5］薛利峰.基于齿轮-连杆组合机构的曲轴复合车削刀架系统研究［D］. 武汉：武汉理工大学图书馆，2012.

［6］邹蕾.曲轴复合车削工艺试验装置误差因素分析与研究［D］.武汉：武汉理工大学图书馆，2011.

［7］吴石林.误差分析与数据处理［M］.北京：清华大学出版社，2010：54 -55.

［8］王忠.平行四边形机构的拓展及其应用［J］.机械设计，2005，22(12)：57 -58.

［9］闵学习，贾育秦.齿轮五杆机构位置误差分析［J］.机械工程师，2011(9)：36 -37.

［10］周建兴. Matlab 从入门到精通［M］. 北京：人民邮电出版社，2012：152 -157.