随机条件下一个网络选址问题的模型及算法

何方国

(黄冈师范学院 数理学院，湖北 黄冈438000)

选址问题是在运筹学和管理科学领域普遍存在的决策问题，主要研究如何选择设施的数目和最优位置来为用户提供相应的服务。1909 年，WEBER 研究了在平面上确定一个仓库的位置使得仓库与多个顾客之间的总距离最小的问题，标志着选址理论研究的开始。1964 年HAKIMI 提出了网络上的p-中值问题，激发了选址问题的研究，从此该问题的研究开始活跃起来。选址研究中的典型问题，如Weber 问题、中值问题、覆盖问题、中心问题、多目标选址、竞争选址、选址-分配和选址-路线等，都是被广泛关注和深入研究的热点课题，研究结果也较为成熟［1-2］。笔者以物流网络为例讨论选址问题。在物流网络中，可以用节点(供货点、需求点)和有向边(运输路线)构成的网络或有向图表示。选址问题是物流网络优化设计的核心，因此相关研究较多［3-5］。在现有的研究中，绝大部分是在确定性需求条件下构造的确定性模型。随着社会经济的发展及市场竞争环境的日益复杂，需求动态变化的特征日益明显。确定性选址模型不再适应动态变化的需求特征，因此能描述需求动态变化特征的不确定性模型就应运而生。笔者提出了一个需求与供给不确定的网络选址模型，并为求解模型给出了一个算法。

1 问题的描述与数学模型

考虑一个物流网络由m个分销点和n个客户组成，根据客户的需求，货物从分销点运到需求点。在客户的需求量和分销点供货量呈随机需求与供应特征的情况下，在给定的m个候选位置中确定分销点的个数和分销点的位置，达到满足每一个客户需求的要求，同时保证网络中所有的费用和成本之和达到最小。为了方便建立数学模型，作出以下基本假设：①各客户需求量和各分销点供货量为随机变量，并且服从已知均值和方差的正态分布。②分销点的候选位置建设费用已知。③每个需求点只由一个分销点供货，且总需求不超过分销点总的供货能力。其中涉及到的变量定义如下：i为第i个分销点，i=1，2，…，m;j为第j个需求点(客户)，j=1，2，…，n;di为分销点i的建设成本;ξi为分销点i的供货能力，ξi～N(μi，);ηj为客户j的需求量，ηj～N(μ~j，);cij为分销点i与客户j之间的单位物流费;αi为给定的置信水平，或称满意率。决策变量包括：

优化问题的目标函数为：

其中，第一部分为分销点与客户之间的物流费用，该费用与需求量成正比，第二部分为分销点的建设费用。由于目标函数含有随机变量ηj，按式(1)求Z的最小值是无意义的，因此建立有机会约束的期望值模型(模型1)：

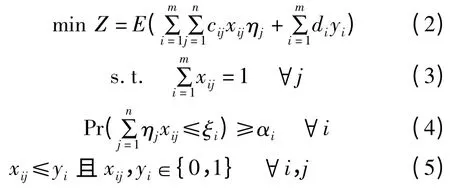
模型优化的目的是在满足一系列机会约束的前提下使得总费用期望值最小。式(3)表示每个客户被且只被一个分销点服务;式(4)限定与某个分销点存在供需关系的客户的总需求量不超过该分销点供货量的概率大于αi;式(5)表示客户只能分配给选定的分销点。这种选址问题具有广泛的代表性，不仅在物流网络而且在通信网络及电力网络中也有应用［6-8］。

2 不确定性模型的转化

不确定性模型转化是一个随机规划问题，模型中需求供给满足正态分布，该模型可以转化成确定性的等价模型。

定理1 设ξi和ηj分别为服从正态分布且为相互独立的随机变量，则式(4)有：

证明 令g(x)=∑jηjxij-ξi，显然g(x)服从正态分布，且期望和方差分别为E(g(x))=这样可以得到变量：

η 服从标准正态分布，因此：

其中，Φ-1为标准正态分布函数的逆。假设机会约束有Pr{η1x1+η2x2+η3x3≤ξ}≥0.95 ，其中η1，η2，η3，ξ 分别服从正态分布N(1，1)，N(2，1)，N(3，1)和N(4，1)。由于Φ-1(0.95)=1.645，则可得其等价形式为：

式(4)通过等价变换为确定性的不等式后，仍是一个非线性优化问题。希望通过近似线性化之后变成一个线性优化问题。根据数学归纳法，可以证明下列结论成立。

定理2 若mi(i= 1，2，…，l)为正数，则且mi相等时取等号。

定理2 表明，当mi较小或者是相差不大时，可以用近似表示而在研究的问题中标准差σi都较小且相差不大，因为正常情况下需求量不会有很大的波动，实际上这个前提比较容易满足。因此约束适当放松成线性约束。这样把表示成

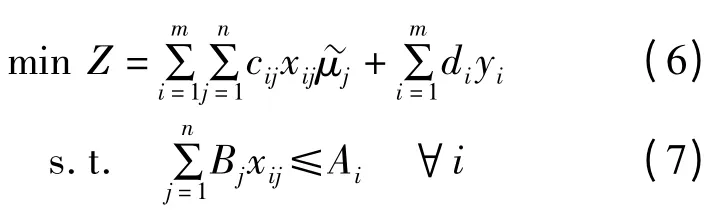
且满足式(3)和式(5)。

3 拉格朗日松弛法求解

对于不同的选址问题有不同算法［9-10］。笔者利用次梯度搜索结合拉格朗日松弛方法来求解。首先对限制条件式(3)和式(7)进行松弛得到拉格朗日松弛问题，并求解得到原问题的一个下界ZLB;其次根据当前的可行解得到原问题的一个上界ZUB;然后利用次梯度法调整拉格朗日乘子得到原问题的上下界并校正，直到得到一个可接受的近似解或迭代次数足够多则算法停止。解的质量由相对对偶间隙(ZUB-ZLB)/ZLB来衡量。

通过拉格朗日乘子将约束条件式(3)和式(7)转移到目标函数中。原问题的拉格朗日松弛问题为：

显然L(λ，γ)是式(6)最优值的一个下界。拉格朗日乘子γi，λj在模型中起到了影子价格的作用，反映了对违反供需平衡约束的惩罚。模型经过松弛转换后，供需之间的依赖关系只反映在式(8)中。利用拉格朗日松弛法，可得到式(8)对偶函数如下(约束条件相同)：

若令Z*为原问题的最优解，则有L(λ，γ)≤D≤Z*。所得的松弛问题与原问题的目标函数比较，松弛问题改变了目标函数中xij的系数。在最小化松弛问题的过程中，如果xij的系数足够小，能够抵消yi所带来的目标函数值的上升，则yi=1，否则yi=0。松弛问题的物理意义在于通过拉格朗日乘子建立了需求与建设成本之间的关系。如果需求所带来的费用压力足够大，就建设某个分销点;否则不建设该分销点。基于该分析，对给定的拉格朗日乘子γi，λj，确定yi，xij的方法(即解松弛问题式(8))如下，令：若Ki＜0，则yi=1，否则yi=0;若yi=1 且Cj＜0，则xij=1，否则xij=0。

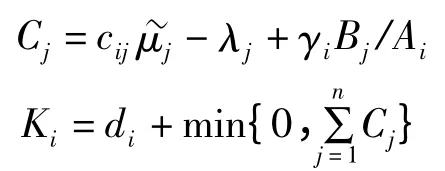
因此求解模型2 的整个算法步骤如下：

(1)设k=0，选取确定的拉格朗日乘子γi，λj，ZLB= -∞，ZUB= +∞。

(2)求解松弛问题式(8)得到yi，xij，由式(9)计算得到原问题的一个下界如果得到的解既满足可行性条件xij≤yi，又满足互补松弛性γi(∑Bjxij-Ai)=0，或者说存在一个次梯度为0，则该解是最优解，算法停止;否则校正下界ZLB=

(4)若存在可接受的θ，使得|(ZUB-ZLB)/ZLB| ＜θ，或迭代次数已经达到了某个极限，则停止迭代。

(5)利用次梯度算法调整拉格朗日乘子，其中θk为迭代第k步的步长。

(6)令k=k+1，返回步骤(2)。

4 算法的实例

给定5 个可能的分销点的候选位置，同时给定10 个已有的客户点，即m=5，n=10。假设每个客户只能由一个分销点提供服务，分销点的供应量和客户的需求量分别服从正态分布N(μi，σi2)，i=1，2，…，5 和N(μj，σj2)，j=1，2，…，10。设所有随机变量的方差均为1，给定的置信水平(客户满意率)均不低于85%。分销点的建设成本di(i=1，2，…，5)和单位物流费用矩阵Cij(如表1 所示)，μi={42，55，65，60，50};μj={18，23，14，15，20，11，19，10，20，16};di={32，37，29，38，34}。用Matlab 编程实现拉格朗日松弛算法。计算时首先转化成确定性模型，然后转化为整数线性规划。应用上述算法得到：yi={0，1，1，0，1}，确定了网络选址的位置和数量;网络选址的费用和为574。得出的解满足原问题的约束条件，是原问题的可行解，同时也是原问题的近似最优解。此时xij为：x23=x26=x28=x29=x32=x35=x37=x51=x54=x5，10=1，其余为0。

表1 供货点i 到需求点j 的单位物流费用

5 结论

笔者对不确定的供需物流网络优化问题进行了研究，按照成本最低化原则，给出了包含不确定参数的选址数学模型。当产品的供应量和需求量均满足正态分布时，以随机理论为基础，证明了在正态分布的情况下，该问题的数学模型可以转化为确定性的数学模型。采用拉格朗日松弛算法对系统费用进行优化。通过将原问题简化，把一个非线性优化问题简化为线性问题进行求解，然后利用次梯度搜索结合拉格朗日松弛方法来求解，获得总费用最小的分销点数量和位置的选择方案，以及分销点与客户之间的供需关系。实例数值结果证明了该模型和算法的有效性。

［1］王非，徐渝.离散设施选址问题研究综述［J］. 运筹与管理，2006，15(5)：64 -68.

［2］王丹，马云峰. 竞争与合作设施并存的最大覆盖选址问题［J］. 武汉理工大学学报：信息与管理工程版，2010，32(4)：628 -630.

［3］杨丰梅，华国伟.选址问题研究的若干进展［J］. 运筹与管理，2005，14(6)：1 -6.

［4］蒋利军，蒋明，赵正佳.配送中心选址问题研究文献综述［J］.物流科技，2008(4)：31 -33.

［5］万波.基于层级模型的嵌套型公共设施选址问题研究［J］. 武汉理工大学学报：信息与管理工程版，2012，32(2)：218 -222.

［6］吕静，樊锁海.会议选址问题的优化模型［J］. 数学的实践与认识，2011，41(3)：141 -149.

［7］FARAHANI R Z.Multiple criteria facility location problems：a survey［J］.Applied Mathematical Modelling，2010(6)：1689-1709.

［8］ANDREAS K.Facility location models for distribution system design［J］. European Journal of Operational Research，2005，162(1)：4 -29.

［9］朱思峰.多目标优化量子免疫算法求解基站选址问题［J］.华中科技大学学报，2012，40(1)：49 -53.

［10］沈萍，陈燕.物流配送中心选址问题的0 -1 规划并行算法［J］. 计算技术与自动化，2012，31(3)：131 -133.