可分离二次规划问题的自适应交替方向乘子法

唐 瑜，张守贵

(重庆师范大学 数学科学学院， 重庆 401331)

0 引言

交替方向乘子法是求解可分离凸优化问题的一种经典方法。该算法利用目标函数的可分离性，将原问题分解成多个极小化子问题，然后通过迭代交替求解[1-3]。交替方向乘子法有很好的理论基础，其收敛性和计算复杂性已得到深入研究，且应用广泛[4-5]。理论和实际应用证明，拉格朗日乘子法是求解最优化问题的一种有效方法[6-7]。该算法的主要优点在于每次迭代均把所求解的问题分解为2个子问题，迭代矩阵始终保持不变[8-9]。另外，算法对罚参数具有全局收敛性。然而，该方法的罚参数取值对收敛速度影响很大，罚参数太小或太大都将极大地减缓收敛速度，因此在实际应用中面临如何优化选择罚参数的问题[10-11]。

针对交替方向乘子法求解具有等式约束的可分离二次规划问题，对罚参数的选择给出了具体可行的自适应方法[12]。引入1个罚参数和增广拉格朗日乘子法表示的极小值问题，再用交替方向乘子法求解，得到1个简单的两步迭代方法。该方法的每次迭代均是先求解2个简单的极小值问题，在此基础上更新拉格朗日乘子。为了克服罚参数对收敛速度的影响，给出基于平衡原理选择合适罚参数的自适应法则，该法则已成功应用于投影算法和Uzawa块松弛算法[13-15]。在上述交替方向乘子法的基础上，进一步得到类似的法则，自动选取使算法收敛较快的可变罚参数，从而显著提高算法性能。最后，通过数值算例验证算法的可行性和有效性。

1 交替方向乘子法

考虑具有等式约束的可分离二次规划问题：

(1)

其中：A∈Rr×n，B∈Rr×m是行满秩矩阵；b∈Rr是一个给定列向量；f(x)、g(y)均为二次函数；X⊂Rn、Y⊂Rm为非空闭凸集。显然，问题(1)存在唯一最优解(x*,y*)。

引入问题(1)的增广拉格朗日函数：

lρ(x,y,λ)=f(x)+g(y)+

λT(Ax+By-b)+

其中：λ∈Rr是拉格朗日乘子；ρ>0是给定的罚参数。

采用交替方向乘子法求解，将原问题进行等价变形和分解，并交替求解，使每个极小化问题以更简单的形式有效解决，具体算法过程见算法1[1]。

算法1交替方向乘子法(ADMM)

步骤1给定初始值{y0,λ0}∈Rm×Rr，ρ>0，令k=0。

步骤2计算xk+1∈Rn，使得对∀x∈Rn有

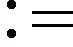
(2)

步骤3计算yk+1∈Rm，使得对∀y∈Rm有

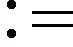
(3)

步骤4更新拉格朗日乘子

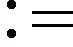
(4)

步骤5对给定的误差限ε>0，若满足

则停止迭代，得到数值解(xk+1,yk+1)；否则，令k=k+1，返回步骤2。

对于上述交替方向乘子法，在文献[1]中已得到一些重要结果。最优解(x*,y*)和拉格朗日乘子λ*满足

(5)

引理1 由交替方向乘子法得到的序列{xk,yk,λk}满足

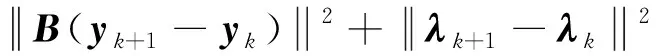
(6)

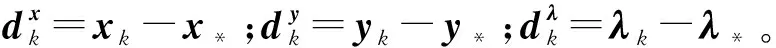
(7)

则当k→∞时，右端收敛于0。

引理1和引理2的证明过程参见文献[1]。

2 自适应交替方向乘子法

交替方向乘子法对所有正的罚参数都收敛，通常取固定参数。然而，交替方向乘子法的收敛速度高度依赖于罚参数，而且在具体问题中很难选择合适的罚参数。针对如何选择合适罚参数的问题，提出一种改进交替方向乘子法，即利用自适应法则和迭代结果近似选取合适罚参数来代替固定参数[12-15]。

在引理1中，用ρk代替ρ，则由交替方向乘子法生成的序列{xk,yk,λk}满足不等式：

||λk-λ*||≈ρk||B(yk-y*)||

分别用λk+1和yk+1替代λ*和y*，可得

||λk-λk+1||≈ρk||B(yk-yk+1)||

于是得到选择罚参数ρk+1的基本思路。对于一个给定的正常数τ，如果

ρk||B(yk-yk+1)||>(1+τ)||λk-λk+1||

则在下一次迭代中减小ρk；如果

则在下一次迭代中增大ρk。

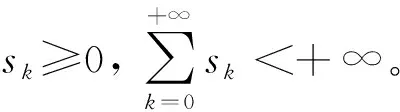
综上，改进交替方向乘子法即自适应交替方向乘子法算法过程见算法2。

算法2自适应交替方向乘子法(SADMM)

步骤1给定初始值{y0,λ0}∈Rm×Rr，ρ>0，ρk=ρ>0，令k=0。

步骤2计算xk+1∈Rn，使得对∀x∈Rn有

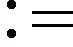
(8)

步骤3计算yk+1∈Rm，使得对∀y∈Rm有

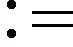
(9)

步骤4更新拉格朗日乘子

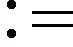
(10)

步骤5选择罚参数ρk+1

步骤6对给定的误差限ε>0，若满足

则停止迭代得到数值解(xk+1,yk+1)；否则，令k=k+1，返回步骤2。

3 收敛性分析

为了证明自适应交替方向乘子法的收敛性，在此先给出引理3。

记

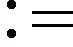
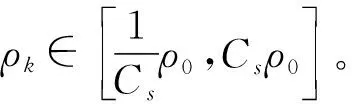
得到有关收敛性结果的定理1。

定理1当k→∞时，由改进交替方向乘子法得到的序列{xk,yk,λk}收敛于{x*,y*,λ*}。

(11)

(12)

因此，由式(11)和式(12)得

(13)

从而有

(14)

(15)

对不等式(13)两端求和，结合式(15)得到

(16)

这表明，

(17)

由式(8)—(10)得到

(18)

把式(18)的最后1个式子代入其余2个等式得到

(19)

这样就有

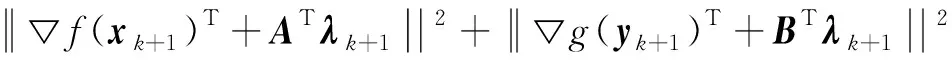
由式(17)得到

当k→∞时，序列{xk,yk,λk}的极限满足问题的最优化条件(5)，从而收敛于{x*,y*,λ*}。

4 算例分析

利用自适应交替方向乘子法求解可分离二次规划问题。迭代过程中，利用迭代数据自动调整罚参数，用变参数ρk代替固定参数ρ，从而达到提高算法效率的目的[12-15]。对于交替方向乘子法(算法1)，取固定罚参数ρ；对于自适应交替方向乘子法(算法2)，序列{sk}按照如下方式得到：

其中：cmax是一个正常数；ck表示ρk改变的次数，即

显然，序列{sk}满足引理3的条件。在数值算例中，取τ=2，cmax=100。

考虑求解等式约束的二次规划问题：

(20)

对于不同的初始罚参数取值ρ，表1分别对n=10 000，20 000，40 000时的交替方向乘子法和自适应交替方向乘子法所需迭代次数进行了比较，表中“—”表示迭代次数超过500次。表2分别给出了迭代所需的CPU运行时间，时间单位为s。表1和表2的结果表明，自适应交替方向乘子法不仅使迭代次数有效减少，收敛速度更快，而且非常稳定。自适应交替方向乘子法的收敛速度和CPU运行时间几乎不受初始参数ρ的影响。

表1 2种算法的迭代次数

表2 2种算法的CPU运行时间

5 结论

在求解具有等式约束二次规划问题的交替方向乘子法的基础上，提出了自适应罚参数算法。交替方向乘子法的主要优点是迭代计算简单，对所有罚参数都具有全局收敛性。然而，交替方向乘子法的收敛速度高度依赖罚参数的取值，而且事先很难选择合适的罚参数。为了提高算法的性能，提出了采用可变罚参数的自适应交替方向乘子法。该方法在迭代过程中利用迭代数据自动调整罚参数，加快收敛速度。数值算例表明了新算法具有优越性。