智能微调的混合动力汽车能量管理策略研究

赖晨光，庞玉涵，胡 博，杨小青，张苏男，黄志华

(1.重庆理工大学 汽车零部件制造及检测技术教育部重点实验室， 重庆 400054；2.重庆理工大学 车辆工程学院， 重庆 400054)

0 引言

随着社会和科技的发展，能源危机和环境污染问题日趋严重，在此环境下新能源汽车迅速发展[1]。混合动力汽车是新能源汽车的一种，动力系统包含2种或多种动力装置，最常见的组合是发动机与电动机，在保障续航里程的同时，还能减少油耗和降低排放[2]。

混合动力汽车动力系统的好坏主要取决于能量管理策略，好的能量管理策略能够在满足动力性的前提下同时减少油耗。如图1所示，目前的控制策略主要分为3种[3]：基于规则、基于优化和基于学习。基于规则的控制策略是基于启发式、直觉、人类专业知识或者数学模型而设计的，并且通常不需要预先定义的驾驶循环的先验知识，但需要花费大量的时间进行人为调参，适用范围受到行驶工况的限制，已有很多学者将其应用于混合动力汽车[4-6]。基于优化的控制策略由于适应好、调参简单等特点受到诸多学者的关注。Serrao[7]对动态规划[8]、庞特里亚金最小原理[9]和等效能耗最小策略[10]3种已知的优化算法进行了比较分析。全局最优的动态规划(dynamic programming，DP)由于需要知道全局信息才能求解，所以在实际应用中存在一定的局限性，通常作为其他策略的比较基准[11]。国内外许多学者将庞特里亚金最小原理(Pontryagin’s minimum principle，PMP)应用于混合动力汽车能量管理问题上，均取得了不错的控制效果[12-14]。PMP解决的是离散问题，学者们在此基础上提出了等效能耗最小策略(equivalent consumption minimization strategy，ECMS)，用于解决连续的问题[15]。随着人工智能技术的发展，基于学习的方法也广泛应用于混合动力汽车能量管理问题的研究。Liu等提出了基于Q-learning和Dyna算法的混合动力车辆自适应能量管理策略，并取得优于基于规则能量管理策略的控制效果[16-17]。Sciarretta等[18]提出了一种基于深度强化学习的能量管理策略，可以学习直接从状态中选择动作，而无需任何预测或预定义规则，并在仿真环境中验证策略在燃油经济性方面的有效性。

图1 混合动力汽车能量管理策略分类框图

目前国内外利用深度强化学习算法强大的自学习能力去优化已有的控制策略的研究较少，往往是通过深度强化学习算法直接控制，但是控制效果不是很理想，需要大量的学习时间。李家曦等[19]利用DDPG算法直接调整ECMS的等效因子，取得了接近A-ECMS的控制结果，在油耗上也有所改善。陈渠等[20]将DP算法与机器学习相结合，提出了一种全新的控制策略，该策略的燃油经济性较基于规则的能量管理策略有明显的提升。

基于上述的一些研究，结合深度强化学习算法与自适应等效能耗最小策略，提出了基于DDPG微调的能量管理策略。利用DDPG考虑更完善的汽车状态来微调A-ECMS输出的等效因子，实现电池SOC保持，整车油耗降低。

1 混合动力汽车模型

P2构型混合动力汽车的电机、发动机和变速器位于同一轴线上，通过对离合器与P2模块的协同控制可以让汽车在纯发动机、纯电动、能量回收、加速助力4种模式下工作。图2为P2混合动力汽车结构示意图。搭建整车仿真模型的参数如表1所示。

图2 P2混合动力汽车结构示意图

表1 整车及动力部件参数

1.1 动力总成模型

在给定车速v后，需求功率Prep由所需克服的道路滚动阻力Ff、空气阻力Fw、坡度阻力Fj、加速阻力Fi通过以下公式计算得到：

Prep=(Ff+Fw+Fi+Fj)v

(1)

(2)

式中：v为车速；m为车辆质量；f为滚动阻力系数；α为道路的坡度；g为重力加速度；Cd为空气阻力系数；A为迎风面积；δ为质量系数。

混合动力汽车的需求功率由发动机和电池共同提供：

Prep=(Peng+Pbatηm)ηT

(3)

式中：Peng为发动机输出功率；Pbat为电池功率；ηm为电动机效率；ηT为变速器和车轴的效率。

1.2 发动机建模

发动机的燃料消耗与发动机输出扭矩Peng和发动机转速neng有关，所以燃料消耗率表示为：

(4)

汽车发动机在时间t内的总油耗可由燃油消耗率积分得到：

(5)

1.3 电机建模

电机作为电动机时，通过电池组供电与发动机共同提供扭矩，输出功率可以由输出转子端转速和转矩乘积决定；作为发电机时，通过回收发动机多余的输出功率给电池组充电，发电功率由定子端电压和电流乘积决定。

电动状态时，电机转矩Tmot与转速ωn满足：

(6)

发电状态时，电机转矩Tmot与转速ωn满足：

Pmot=Tmot·ωn·ηm

(7)

1.4 电池模型

采用容量为5.3 Ah的磷酸铁锂电池，整个电池组由72个单体电池串联组成。忽略温度对电池组的影响，使用内阻建模的方法建立电池组模型。电池组输出功率Pbat和输出电压Ubat为：

(8)

式中：Voc为开路电压；rint为电池内阻；Ibat为电池电流。由式(8)可知，当电池组输出功率已知时，电池电流可表示为：

(9)

电池荷电状态SOC是电池组的重要参数，是电池所剩电量和电池总容量Qbat之比：

(10)

式中：Ibat为电池电流，本文选择SOC作为能量管理问题中的状态变量之一。联立式(9)和(10)可得SOC微分，重新表示为：

(11)

1.5 建模约束

为了保证部件的安全性和可靠性，整车动力系统需要满足相应的物理约束，即发动机与电机的输出转速、转矩，SOC的变化范围、电池功率应该在约束范围内工作：

(12)

2 等效燃油消耗最小控制策略

等效燃油消耗最小控制策略(equivalent consumption minimization strategies，ECMS)基于的理念：电量维持型的混合动力汽车的电池初始SOC值和最终SOC值之间的差异非常小，相对于所使用的总能量可以忽略不计，所以最终所有的能量消耗均来自燃油。电池等同于一个可逆的辅助油箱，消耗的电能终将通过发动机的多余输出功率补充回来。

ECMS的关键思想是，在放电过程中，等效燃油消耗可以与电能的使用联系起来。未来(或过去)电能消耗可以等效为燃油消耗量，与当前实际燃油消耗量求和可以得到瞬时等价燃油消耗。以功率的形式定义ECMS的瞬时成本：

Peqv(t)=Pfuel(t)+s(t)Pbatt(t)

(13)

式中：s(t)是等效因子，其作用是把电池的功率转为等效的燃油功率。实际上，等效因子代表燃油转化为电能的效率链，也是电能转化为等效油耗的效率链，因此，它会随着动力系统的运行条件而改变。根据等效因子是否会实时变化，将ECMS分为恒等效因子ECMS和A-ECMS。

恒等效因子ECMS将等效因子看作一个恒定的常数，该常数往往是在离线实验中通过迭代发现最优值求得。但是离线实验得到的等效因子往往只适用于一段工况或者同类型的各工况，没办法满足混合动力汽车复杂的行驶工况。

基于SOC反馈的A-ECMS是通过一个PID控制器根据SOC与SOC目标值的差值来输出一个可实时变化的等效因子，这是一种最常见的A-ECMS方法，如图3所示。该种方法由于只单一地考虑SOC的变化，没有考虑复杂工况的行驶需求以及汽车本身的状态，所以控制效果并不是很好，本文将利用DDPG算法对此控制策略进行优化探索。

图3 基于PID的A-ECMS逻辑图

3 强化学习理论

3.1 强化学习

强化学习主要应用于控制领域，它的本质是试错学习，通过不断地探索与环境交互获取状态和奖励来优化自身的策略。从图4中可以看出，在t时刻状态St下，智能体根据已有的策略选取动作At，环境在t+1时刻到达状态St+1，同时反馈一个奖励Rt+1给智能体，通过此循环不断优化奖励值得到接近最优的控制序列。

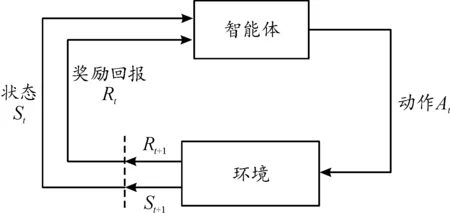
图4 强化学习过程框图

3.2 深度强化学习

普通的强化学习是表格化动作、状态和奖励，通过与环境交互对状态下采取动作所获得的奖励值进行迭代，直至收敛。这种方法受到储存空间、状态与动作的维度的限制，让强化学习只能用于较为简单的离散动作控制。深度强化学习早在2015年就已经被提出来了，谷歌Deepmind团队将其用于解决围棋问题，在与人类的比赛上，成功击败人类顶级棋手，让强化学习受到了学者们的广泛关注[21-22]。如图5所示，智能体动作的选择，以及评价动作选取的优劣都是通过神经网络来实现的，提高了算法的计算能力，为强化学习应用于更加复杂的环境提供了基础。

图5 深度强化学习逻辑图

3.3 深度确定性策略梯度算法

2016年，在DQN算法的基础上结合Actor-Critic和确定性策略梯度，谷歌Deepmind团队提出了DDPG算法，该算法可以在连续空间上进行控制，动作直接由神经网络输出[23]。如图6所示，DDPG算法总共有2套Actor-Critic网络，一套为评估网络，另一套为目标网络。

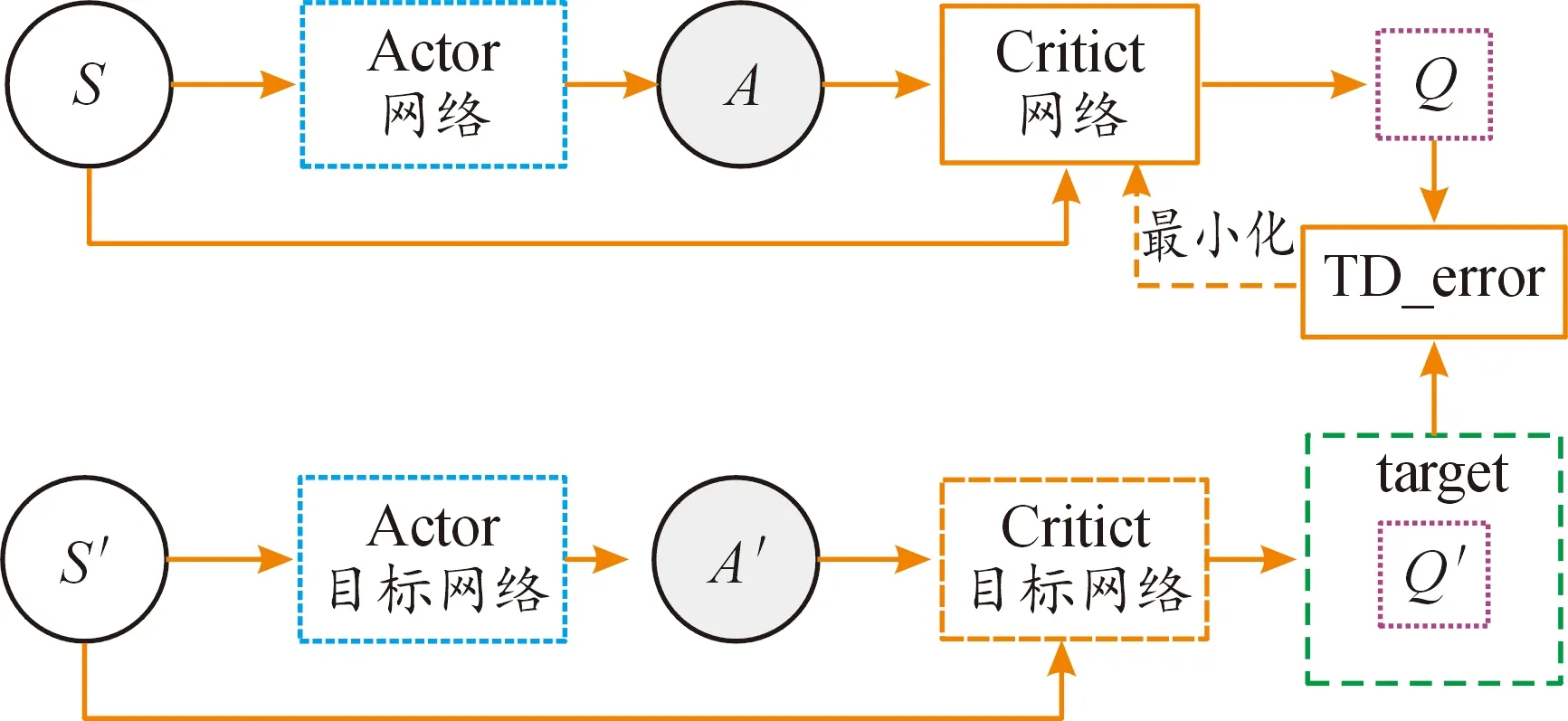
图6 DDPG算法逻辑图

Actor网络目的是找出动作A，令输出的Q(S,A)最大化，Critic网络是根据当前的动作A和状态S计算出Q(S,A)。算法更新时，智能体先冻结住目标网络，从换环境获得状态，通过评估网络计算出Q值，同时也通过目标网络计算出Q′值，最小化Q和Q′的差值来更新评估网络。当智能体与环境交互经过时间T之后，把评估网络的网络参数赋值给目标网络。

DDPG算法的伪代码如下：

1： Randomly initialize critic networkQ(s,a|θQ) and actorμ(s|θμ) with weightsθQandθμ

2： Initialize target networkθ*andμ′ with weights

θQ←θQ,θμ←θμ

3： Initialize replay bufferR

4： for episode = 1 toMdo

5： Initialize a random processNfor action exploration

6: Receive initial observation state

7: fort= 1 toTdo

8: Select actionat=μ(st|θμ)+Ntaccording to the current policy and exploration noise

9: Execute actionatand observe rewardrtand observe new statest+1

10: Store transition (st,at,rt,st+1) inR

11: Sample a random mini-batch ofNtransitions (si,ai,ri,si+1) formR

12: Setyi=ri+γQ′(st+1,μ′(si+1|θμ)|θQ)

13: Update critic by minimizing the loss:

14: Update the actor policy using the sampled policy gradient:

▽θμμ(s|θμ)|si

15: Update the target networks:

θQ←τθQ+(1-τ)θQ

θμ←τθμ+(1-τ)θμ

16: end for

17: end for

4 基于深度强化学习微调的能量管理策略

A-ECMS根据电池SOC的实时变化对等效因子进行实时地修改来控制发动机与电机的输出功率。但A-ECMS对汽车自身的状态考虑较少，仅考虑了电池SOC的变化，所以本研究通过DDPG算法考虑汽车自身的状态来获得一个等效因子修正量，然后与PID控制器输出的等效因子相加得到最终的等效因子来控制发动机与电机的输出功率，整个控制逻辑如图7所示。从图7中可以看出，基于DDPG微调的能量管理策略在考虑电池SOC的基础上，增加了上一时刻的发动机和电机的输出扭矩和当前时刻的需求扭矩。

图7 基于DDPG微调的A-ECMS能量管理策略逻辑图

结合文献和源代码的理解[19,24]，搭建基于DDPG算法框架的部分超参数，如表2。DDPG中神经网络的结构如图8，Actor网络和Critic网络均由输入层、3个隐藏层、输出层构成，其中每一层隐藏层包含120个神经元，神经层之间均采用全连接。

表2 DDPG超参数

DDPG记忆库需要存储由当前状态St、该状态下所执行的动作At、动作执行后得到的奖励Rt以及环境所达到的下一状态St+1组成的一个四元组(St,At,Rt,St+1)。所以，接下来分别对状态、动作、奖励进行定义。

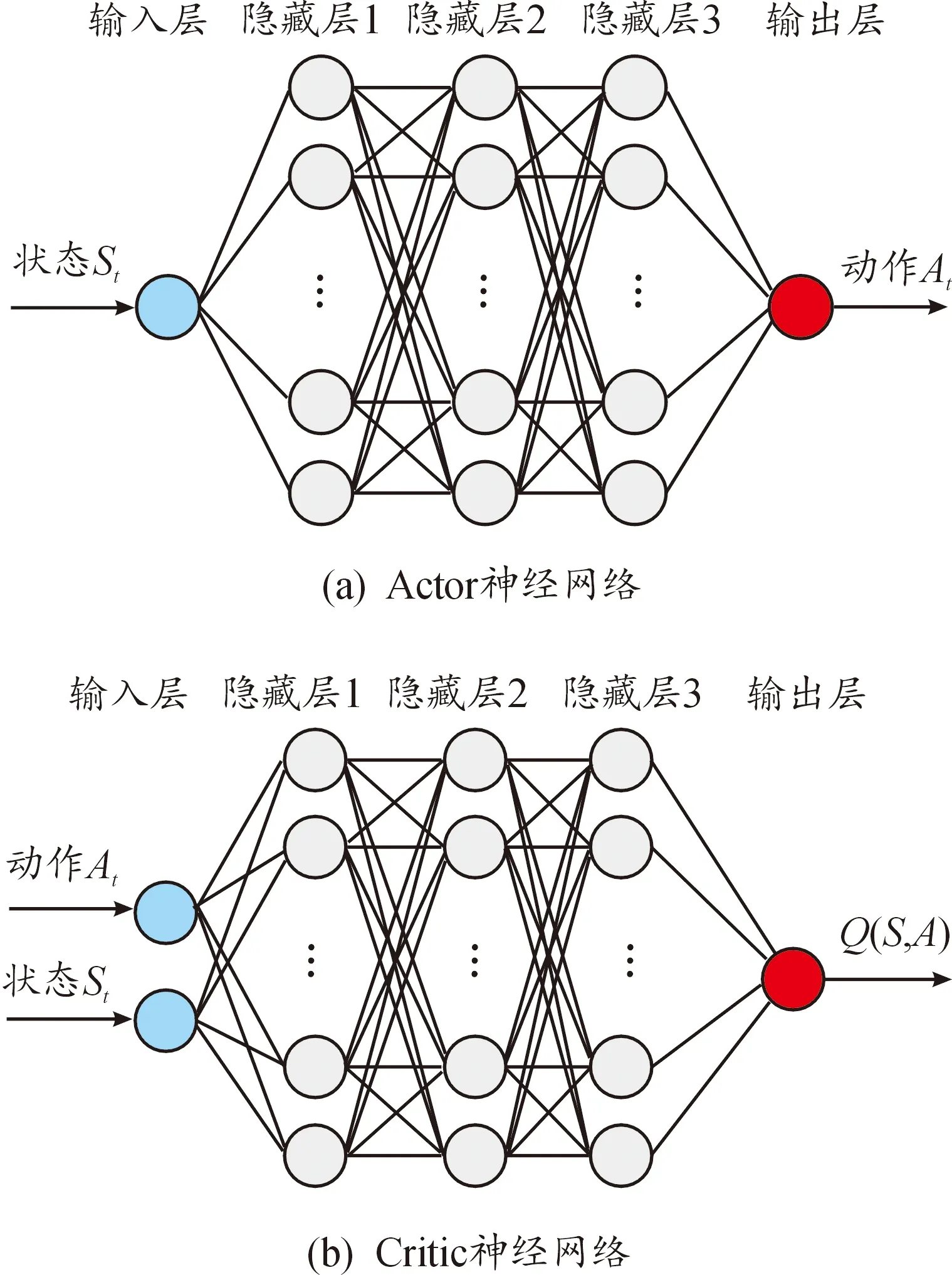
图8 Actor和Critic神经网络结构示意图

状态St：混合动力汽车的驾驶循环是连续变化的，所以为了更加准确地描述混合动力汽车的状态，状态应选择连续变量。同时，如何精确描述行驶状态的变化具有很大的挑战性，所以应该选择能够定义混合动力汽车的行驶周期状态的状态变量。本研究选取了6个状态变量：电池SOC、PID控制器输出的等效因子、汽车的需求扭矩、上一步的输出动作、上一步ECMS的电机和发动机的扭矩控制量。选择SOC作为状态变量是因为本研究的混合动力汽车是电量维持型的混合动力汽车，所以SOC与汽车油耗息息相关，如何在电量与油耗之间找到最优的平衡点是本研究的目的。选择PID控制器输出的等效因子、汽车的需求扭矩、上一步的输出动作、上一步ECMS的电机和发动机的扭矩控制量作为状态变量是为了更加准确地描述混合动力汽车当前的状态，对等效因子的影响因素考虑更加完善，从而更加准确地修正等效因子。

动作At：通过DDPG控制根据汽车当前的状态对PID控制器输出的等效因子施加一个修正量，从而让ECMS控制器能够更合理地分配发动机电机输出扭矩。

奖励Rt：奖励信号应该与整个模型的优化目标高度相关。本研究的最终目的是在保持电池SOC的基础上尽可能地减少油耗，所以本研究的奖励函数包含了电池SOC和油耗2个关注点，奖励函数设置如下：

rt=exp(-0.7|et|-0.3|it|2)

(14)

式中：et是电池SOC与目标值的差值；it是控制周期内的燃油消耗量。经过调整后，最终将et和it的系数设置为0.7与0.3。为了保证计算的高效性，采用高斯函数的形式对奖励函数进行构建，让奖励值在(0，1)。

5 仿真分析

使用一台搭载Windows 10专业版、64位操作系统、处理器为Intel(R) Core(TM) i5-10400F CPU @ 2.90 GHz、基带RAM为32.0 GB的计算机完成计算任务。在Matlab/Simulink中搭建混合动力汽车仿真模型，通过To Workspace建立数据输出接口，而在Python端通过调用Matlab中的m文件控制混合动力模型，以此循环交互完成仿真实验。

将FTP75循环工况作为DDPG算法的训练工况。FTP75工况是美国环保局在1975年提出来的，用于评估车辆的燃油经济性，分为冷启动、瞬态、熄火浸车、热启动4个阶段，全程平均车速25 km/h，最高车速91.2 km/h，全程用时2 474 s，如图9所示。

图9 FTP75循环工况车速曲线

当算法训练收敛后，将使用NEDC循环工况进行验证，该工况包含了市区和市郊2种工况，具有频繁的加减速和启停，还有持续的加速，也是目前中国正在使用的测试工况，如图10所示。为了证明所提出控制策略的优越性，将基于DDPG微调的A-ECMS能量管理策略同基于规则的ruler-based、深度强化学习(DDPG)、A-ECMS、动态规划(DP)4种能量管理策略分别在电池SOC和等效油耗上进行分析比较。

图10 NEDC循环工况车速曲线

图11是DDPG与DDPG微调的能量管理策略学习曲线。从图11中可以看出，2种控制策略均能通过前期的探索然后收敛，但是两者在收敛回合数和收敛时的奖励均有所不同，具体细节如表3所示。

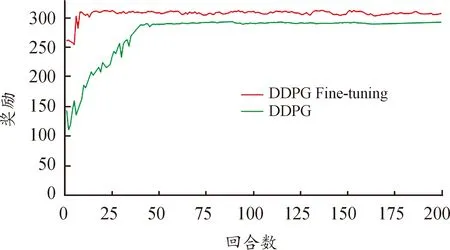
图11 基于DDPG和DDPG微调的能量管理 策略学习曲线

表3 DDPG与DDPG微调学习曲线的细节

由表3可知，DDPG收敛时的回合数为40，DDPG微调收敛时的回合数为16，在训练时间上效率提升60%；同时DDPG微调收敛时的奖励值为308.6，相较于DDPG收敛时的奖励值在动作优化上提高了6.05%(选择的动作越好，所获得奖励越高)。由此可知，将PID控制器的输出动作作为输入状态的DDPG微调的控制策略能够花更短的训练时间得到更好的控制动作序列。

从图12可以看到，动作的随机选取概率随着训练回合数的增加逐渐减小并趋近0。在训练的前期，由于初始化的神经网络参数基本相同，因此需要较大的概率去探索获取更多有用经验，加快收敛速度。在训练的后期，因为当前智能体已经学习到较好的策略，不适合使用较大的动作探索，所以选择较小的动作探索。当概率逐渐趋近于0时，表示智能体所执行的动作基本上都是由DDPG控制器给出，但仍然有极小的随机概率，所以导致奖励曲线在收敛后仍有小波动。

图12 训练过程中动作随机选取概率变化曲线

图13是5种能量管理控制策略在FTP75工况上的SOC的变化曲线。可以看出,5种能量管理策略均能够在一个工况结束后将SOC控制在目标值附近。

图13 不同能量管理策略在FTP75工况的 SOC变化曲线

从表4可以看出，5种能量管理策略的SOC终止值都不相同，因为不同控制策略在控制时会选取不同的等效因子，所以导致控制策略对发动机与电机的扭矩分配不同，最终导致了SOC的差异。从SOC变化曲线可以看出，DDPG微调十分接近最优的动态规划曲线，SOC整体变化较为平缓，对电池有益。而基于规则和DDPG的SOC的变化较为剧烈，前者对电池的利用明显没有后者完善，电池一直在目标值之下工作。

表4 不同能量管理策略在FTP75工况SOC曲线的特征参数

SOC曲线的差异主要在0～250 s(图13黑色虚线方框)和800～1 350 s(图13红色虚线方框)。为了进一步解释SOC曲线的差异，通过导出5种控制策略的发动机与电机扭矩分配图来说明原因。从扭矩分配图可知，基于规则的能量管理策略的发动机多数情况下提供较小的扭矩，剩下的扭矩完全靠电机提供，这导致了整个工况过程中SOC均在目标值之下。从图14(a)黑色方框可以看到，这段时间内几乎全靠电机提供扭矩，对应SOC在0～250 s和800～1 350 s的2次快速下降。图14(d)中黑色方框里发动机与电机的转矩分配则解释了800～1 350 s基于DDPG能量管理策略的SOC曲线连续2次快速下降。从图14(a)-(e)可以看出，不同的能量管理策略对发动机与电机扭矩分配存在较大的差别，DDPG微调的控制效果与动态规划十分接近。

图14 不同能量管理策略的发动机和电动机扭矩分配曲线

图15给出DDPG微调控制过程中实际的车速曲线，DDPG能够很好地满足汽车的动力性要求，只有在最高车速附近时才与参考车速有一点差距，最大差值为0.79 m/s，与参考车速的均方误差为0.03。

图15 基于DDPG微调的能量管理策略的车速曲线

为了进一步证明本研究提出的基于DDPG能量管理策略的优异性，表5给出了5种控制策略在FTP75循环工况上的等效油耗。动态规划的等效油耗最低为7.61 L/100 km，本研究所提出的DDPG微调的等效油耗为7.62 L/100 km，十分接近最优的动态规划，与基于规则的相比，油耗减少了7.07%，与基于A-ECMS和DDPG相比，油耗减少了0.52%。从表5可以看出，DDPG通过训练能够取得与A-ECMS相近的控制结果，由于只保留了小数点后面两位，但是实际结果是DDPG略微优于A-ECMS。图16给出不同能量管理策略的发动机工作点图。从图中可以看出，基于规则的能量管理策略的发动机大多数情况下工作在低扭矩高油耗区域。基于DDPG的能量管理策略与最优的动态规划较为相似，发动机多数情况下在高扭矩低油耗区域工作，而且发动机的扭矩输出比基于规则的输出范围更大。

表5 不同能量管理策略在FTP75工况的等效油耗

图16 不同能量管理策略的发动机工作点图

通过将训练好的控制策略用于没有接触过的全新工况上对比控制结果，看是否能与训练的控制结果一样来验证基于DDPG微调的能量管理策略的适用性。从图17和表6可以看出，不同的能量管理策略在NEDC工况上的控制效果是不同的，但都能将SOC的终止值控制在目标值附近。发动机能长时间工作在高效区间，持续地加速和快速地制动减速，控制策略频繁使用发动机提供扭矩，同时利用多余的扭矩和制动能量给电池充电。

在等效油耗上，本研究提出的基于DDPG微调的能量管理策略在测试工况上一样取得了优异的省油效果。在NEDC工况上，基于DDPG微调等效油耗为7.74 L/100 km，与基于规则的比较油耗减少2.27%，与基于A-ECMS的相比油耗减少0.77%(见表7)。

图17 不同能量管理策略在NEDC工况的SOC变化曲线

表6 不同能量管理策略在NEDC工况的SOC曲线特征参数

表7 不同能量管理策略在NEDC工况的等效油耗

6 结论

在A-ECMS的基础上结合DDPG控制算法考虑更为全面的汽车状态，搭建了基于DDPG微调的能量管理策略，先进行了理论分析，然后通过仿真实验进行验证。由训练过程可知，基于DDPG微调的能量管理策略可以在原有的强化学习的能量管理策略基础上进一步优化发动机和电机的输出扭矩，优化效果提升了6.05%，同时也能够加快整个控制策略的收敛时间，效率提升了60%。在训练工况FTP75以及工况NEDC和FTP72上均取得了优于基于规则和A-ECMS的控制结果，证明了深度强化学习可以与其控制策略结合并取得优于原来的控制结果。通过将训练好的控制策略在不同工况上测试，从测试结果上可以得知，基于DDPG微调的能量管理策略能够在保障优异的控制结果的同时具备很好的可适用性。

本文的研究结果在混合动力汽车的控制策略优化上有参考意义，同时也对强化学习用于优化其他控制策略或者结合提供了思路。后续将会通过第三软件获取交通信息、平均车流速度等信息优化控制策略的控制效果。未来，在有条件的情况下，将进行硬件在环验证和实车实验等。