四轮转向前后梯形优化设计

黄妙华，程 勇

(武汉理工大学 汽车工程学院，湖北 武汉430070)

四轮转向技术作为一种有效的主动安全技术已经得到广泛重视。高速时，前后轮同向转动可改善车辆的操纵稳定性;低速时，前后轮异向转动可减小最小转弯半径，提高车辆的通过性［1-2］。四轮转向技术应用于消防车辆上可帮助车辆通过狭窄的城市路段。商用车四轮转向的研究集中于四轮转向控制策略的研究，主要采用线性二自由度模型，将车辆简化为自行车模型，分析车辆高速的操纵稳定性［3-4］。

转向车辆的四轮模型，考虑了内外侧车轮的干涉问题。建立基于转向梯形参数的评价方法，并分析四轮转向梯形机构的运动瞬心偏差产生原因，优化计算得到了最优的前后梯形参数。

1 运动瞬心偏差

某前轮转向消防车最小转弯半径为8.5 m。将后桥改为转向驱动桥，后转向梯形前置，要求转弯半径减小至5.9 m。前桥参数：两前主销距K1为1.798 m，梯形臂长m1为0.169 m，梯形底角γ1为75.4°。后桥参数：两后主销轴线与地面交线的距离K2为1.68 m，梯形臂长m2为0.281 m，梯形底角γ2为82.2°。前后轴距L=4.5 m［5］。

理想的车轮轴线交于一点，但4 个车轮轴线两两相交产生4 个交点A、B、C和D，如图1 所示。若4 点重合于一点，瞬心偏差最小，车轮的磨损也最小。低速行驶时，车辆处于平衡状态，运动瞬心在四边形区域ABCD中。

存在一点R，使得∠RMD=∠RNC，∠RPB=∠RQC。用f=∠RMD+∠RNC+∠RPB+∠RQC评价瞬心位置偏差;f越小，瞬心偏差越小，车轮磨损量越小。存在一个最小圆，包含交点A、B、C和D，即为当前转向状态的交圆。

图1 瞬心偏差示意图

2 四轮转向梯形机构仿真分析

2.1 前转向梯形优化设计

图2 为前桥梯形示意图，图中A、B为前主销轴线与地面的交点，C、D为梯形拉杆交接点在地面的投影。

整体式转向梯形理想内轮转角θf2与外轮转

角θf1的关系为：

实际的内外轮转角关系为：

其中，有：

图2 前转向梯形示意图

基于Ackerman 定律优化前转向梯形参数，前外轮转角范围为0° ～30°，建立前桥转向梯形的评价函数。

其中，权函数［6］为：

前转向梯形的最小传动角为：

其中，前外轮最大转角A为30°。

考虑到实际装配等要求，选定前桥参数的优化范围，前梯形臂长m1在0.16 ～0.18 m 之间，前梯形底角γ1在67° ～77°之间。最优的前轮轴线交点在后桥轴线附近［7-8］。

如式(2)所示，评价函数f(m1，γ1)是关于m1和γ1的二元函数，每个m1和γ1都对应唯一f(m1，γ1)。在图3 中，线1 处的梯形传动角为30°。A为最优区域，梯形质量最好，且满足最小传动角的要求。前转向梯形质量对梯形底角值敏感，对梯形臂长不敏感。最优区域内中间区域梯形底角值即为最理想的值。优化后的前梯形臂长为0.169 m，前梯形底角为72°。

优化前后的前桥内轮实际转角与理论转角之差的曲线如图4 所示。优化后，在车辆经常使用的小转角区域，内轮实际转角与理论转角更接近。

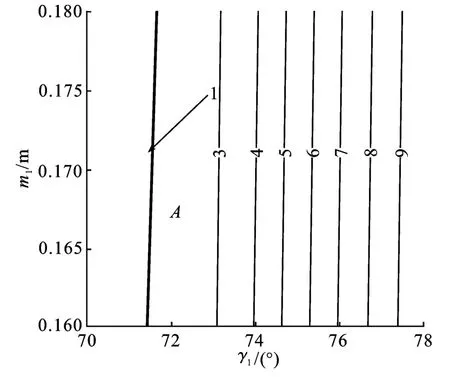
图3 前桥评价函数等高线图

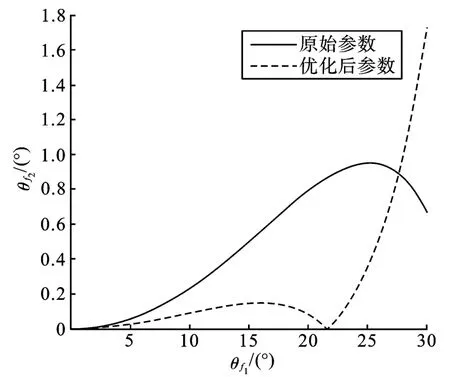
图4 前桥内外轮转角关系

2.2 后转向梯形机构评价方法

转动瞬心的偏差与前后梯形参数和前后轮的实际转角相关，前后轮的转角决定车辆的转弯半径［9-10］。在前后外轮转角分别为θf1，θr1的情况下，建立转角评价函数为：

四轮转向时，前后外轮转角关系为：

建立基于后转向梯形参数的瞬心偏差评价函数为：

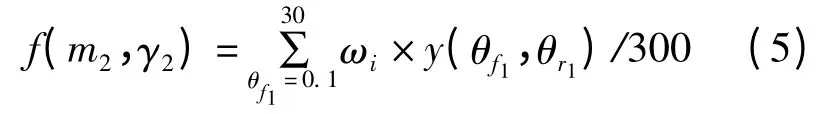
后梯形最小传动角为：

后转向梯形外轮最大转角B=20°。转弯半径为主销偏移距。R+r、R-r分别为转弯半径上限与下限，r为交圆半径。

2.3 后转向梯形仿真分析

由式(5)可得关于后梯形臂长m2和后梯形底角γ2的梯形二元函数f(m2，γ2)，并绘制出后梯形评价函数等高线图，如图5 所示。后梯形臂长m2在0.26 ～0.34 m 之间，后梯形底角γ2在60° ～70°之间。考虑到保证梯形传动效率的要求，后梯形的最小传动角δ2≥30°。由图5 可知，瞬心偏差量对后梯形臂长m2不敏感，对后梯形底角γ2敏感，且梯形底角值越小，瞬心偏差越小。线1 处的后桥梯形最小传动角为30°。在保证传动角要求的前提下，选择图5 中线1 右侧并靠近线1 的区域为最优区域。不改变后梯形臂长m2，选择最佳的后梯形底角值γ2。点2 为优化前后桥参数m2和γ2的位置，评价函数值为1. 092。点3 为优化后后桥参数m2和γ2的位置，评价函数值为0.778 4。优化后评价函数值减小28.7%。优化后的后梯形臂长m2为0.281 m，后梯形底角γ2为62°。

图5 后梯形评价函数等高线图

将原梯形参数与优化后的梯形参数代入式(3)，可得到不同的前后轮转角情况下的瞬心偏差等高线图。图6 为原梯形参数瞬心偏差等高线图，图7 为优化后梯形参数瞬心偏差等高线图。优化后，瞬心偏差最大值减小了46%。

图6 原梯形瞬心偏差等高线图

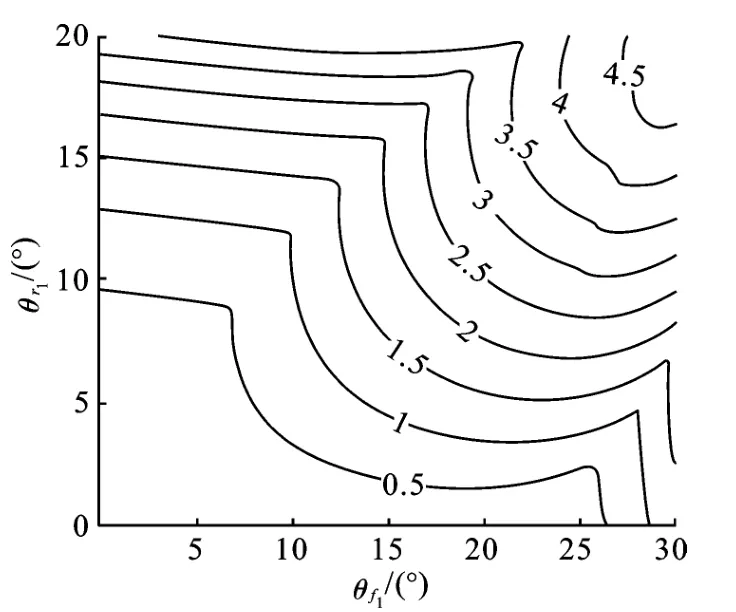
图7 优化后梯形瞬心偏差等高线图

3 结论

运动瞬心偏差量可以用来评价当前状态下的车轮磨损量。用后转向梯形评价方法优化后转向梯形参数，优化后瞬心偏差量明显减小。

优化前的最小转弯半径R为6.07 m，最大交圆半径r为0.40 m。优化后的最小转弯半径R为5.85 m，最大交圆半径r为0.21 m。优化后最大交圆半径减小，转弯半径估算更准确。

［1］胡国强. 汽车四轮转向系统转向特性的研究［D］.武汉：武汉理工大学图书馆，2012.

［2］NAGAI M，UEDA E.Nonlinear design approach to four wheel steering system using neural networks［J］.Vehicle System Dynamics，1995，24(4 -5)：329 -342.

［3］SHIOTSUKA T，NAGAOKA M.Adaptive control of 4WS system by using neural network［J］.Vehicle System Dynamics，1994，23(5-6)：411-424.

［4］徐锐良，曹青梅. 车辆转向梯形机构的参数优化［J］.拖拉机与农用运输车，2008，35(1)：38 -40.

［5］王宵锋，胡涛. 不同整体式转向梯形机构分析方法的对比研究［J］.汽车技术，2005(8)：8 -11.

［6］王望予. 汽车设计［M］. 北京：机械工业出版社，2000：189 -191.

［7］DURSTINE J.The truck steering system from hand wheel to road wheel［J］.SAE ，730039.

［8］SHOICHI S.Four wheel steering system with rear wheel steer angle controlled as a function of steering wheel angle［J］.SAE，860625.

［9］孙营.重型商用车转向系统建模及整车动力学仿真研究［D］.武汉：华中科技大学图书馆，2011.

［10］GERALD M，ROBERT R，FRED W. Optimum ackerman for improved steering axle tire wear on trucks［J］.SAE，912693.