某矿用车动力总成悬置系统隔振性能优化设计

田 晗，颜伏伍，邢 鹏

(武汉理工大学 汽车工程学院，湖北 武汉430070)

汽车行驶过程中的振动来源一般分为外部激励和内部激励两种，其中外部激励是由于路面不平所引起的振动，而内部激励则主要是由发动机工作时的不平衡往复力矩和惯性力力矩或扭矩输出的波动性而引起的振动。目前，评价及优化动力总成悬置系统隔振性能的方法主要有两种［1］：①能量解耦法。以悬置元件的各向刚度作为优化条件，考察动力总成经由悬置系统的能量传递率和解耦度。②振动传递路径法。该方法主要考虑动力总成的振动传递到车身或者车辆内部某些关键点的状况，从而判定悬置系统的隔振性能。与能量解耦法不同，振动传递路径法对整车NVH 性能的改进不仅要考虑悬置元件的各项参数，还需要对车辆本身不利于振动衰减的结构进行优化。

笔者运用能量解耦法，对某矿用车动力总成悬置系统隔振性能进行评估，并以悬置元件各向静刚度作为可变参数，以系统能量解耦率为目标函数，对悬置系统进行了优化计算，为悬置元件的设计开发和性能优化提供了可靠的依据。

1 动力总成悬置系统建模及能量解耦

1.1 柴油机动力总成及悬置系统

笔者选用某矿用车动力总成悬置系统为研究对象，该车车身设计为半承载式，采用以东风康明斯4BTAA 3.9 -C125 发动机为基础的防爆发动机，其最大转矩为280 N·m，对应发动机转速为1 500 r/min;最大转速2 200 r/min 时对应转矩为267 N·m。发动机在原机基础上采用进气关断阀、进气阻火隔栅、气起动机、液压油门、防爆增压器、隔爆型发电机、隔爆缸体缸盖接合面、防爆排气歧管和自动停机保护装置。

发动机悬置采用康明斯4BT 系列的4 点橡胶悬置，左右对称布置，随车架宽度适应性变化。图1 所示为前、后悬置外形及整体布置形式。其中，前悬置橡胶软垫为方形，与xy平面成45°角安装;后悬置橡胶软垫为环形，在y方向有限位。

动力总成模态频率分布一般在6 ～20 Hz 之间，橡胶悬置各向刚度会随振动频率的增加而增大。文献［2］表明，在该频率区间，若橡胶悬置的刚度增加值在7%以内，则对悬置系统整体性能分析影响不是很大。因此，在动力总成及悬置系统建模时，选取悬置元件三向静刚度作为分析参数。以发动机缸体前端面与曲轴中心线的交点为坐标原点，建立坐标系o-xyz。在该坐标系下，动力总成质心坐标为x=437，y=6.9，z=105，前、后悬置各向刚度与安装点位置分别如表1 和表2 所示。该动力总成质量为415 kg，其转动惯量如表3 所示。

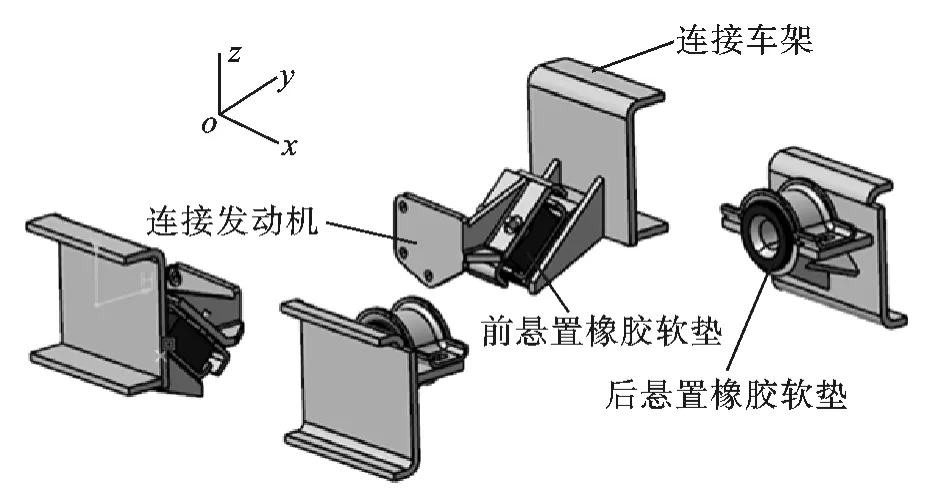
图1 动力总成悬置系统

表1 前、后悬置各向刚度 N/mm

表2 前、后悬置安装点坐标 mm

表3 动力总成转动惯量 kg·m2

1.2 动力总成悬置系统模型的建立

动力总成悬置系统的振动是一个复杂的多自由度的振动过程，其主要激振力来自于发动机内部。在对动力总成及悬置系统进行建模时，需要进行一些必要的简化。李勤等［3］提出了关于发动机悬置系统分析的一种高效建模方法，并通过实例验证了该方法的可用性。从车辆隔振的角度，动力总成及悬置系统的固有频率通常在6 ～12 Hz 之间，在该范围内，动力总成的振动只需考虑其刚体模态。车身及车架的模态频率远高于悬置系统频率，因此将车架部分视为刚体，每个悬置亦简化为无阻尼的线性弹簧。

以动力总成处于静平衡下的质心为坐标原点建立系统坐标系。在工作状态下，动力总成位置可用3 个直角坐标轴x、y、z及绕质心平行于坐标轴的3 个坐标轴转角θx、θy、θz来表示，可用广义坐标矢量表示为：

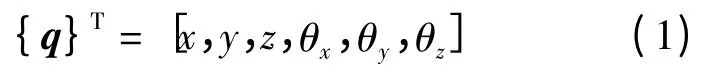
一般情况下，质量-刚度振动系统在无外力作用的情况下，其自由振动的方程式为：

式中：［M］为系统的质量矩阵;［q¨］为系统的广义加速度向量;［C］为系统的阻尼矩阵;［q·］为系统的广义速度向量;［K］为系统的刚度矩阵;［q］为系统的广义位移向量。

由于橡胶悬置元件阻尼不大，其主要作用是降低系统在共振时的最大位移，在小振幅振动状态下，系统阻尼可忽略不计。因此，系统振动微分方程可简化为：

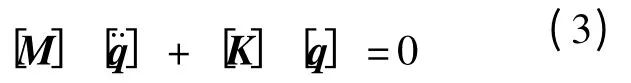
式(2)和式(3)中：

式中：m为动力总成的质量;Ixx、Iyy、Izz为动力总成的惯性矩;Ixy、Ixz、Iyz为动力总成的惯性积。

基于以上动力总成悬置系统基本理论，利用有限元分析软件ANSYS 建立如下简化模型：以重合的质量点单元1、2 表示动力总成刚体，该质量点单元MATRIX27 包含动力总成质量、转动惯量等参数，并设置其刚度为无限大;在各悬置安装点处分别建立沿x、y、z轴的一维弹簧单元COMBIN14;以刚性单元MPC184 连接动力总成质量点和各悬置安装点;各弹簧单元另一端施加全约束［4］，简化模型如图2 所示。

图2 动力总成悬置系统有限元简化模型

1.3 悬置系统的模态能量解耦

动力总成具有沿坐标轴的平移和扭转等6 个自由度，对应的有6 个模态。理想状态下，各模态彼此独立，称为完全解耦。但是在实际工程中，各阶模态互不影响是不可能的。在一定频率下，如果有两种及以上的模态存在，如动力总成即产生绕x轴的扭转，z方向上也会上下振动，还同时伴随y方向的平动。这种多模态并存的情况即称作模态耦合［5］。模态耦合会导致动力总成及悬置系统的振幅增加，在发动机怠速工况下，还有可能使动力总成和悬置系统及车架发生共振，严重影响车辆的NVH 性能。

动力总成在工作过程中，可以看作自由振动，每个模态频率下都有一定的能量。系统在第i阶模态频率下的所有模态能量之和EA为该频率下系统的模态总能量。由式(3)易得到系统在各阶模态频率下的振型{φi}，则有：

式中：ωi为悬置系统第i阶固有频率;mnm为质量矩阵［M］第n行、第m列元素，m=1，2，…，6;n=1，2，…，6。

第i阶模态频率下，作用于第k(k=1 ～6)个广义自由度上的能量Ek为：

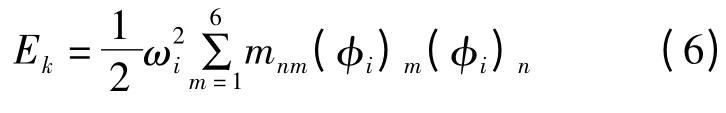
此时，第k个广义自由度上分配到的能量占悬置系统总动能的百分比为：

通过计算动力总成悬置系统各阶模态频率下的η 值，即能量解耦率，可直观地得知该悬置系统隔振性能的好坏。悬置系统优化的过程是通过改变悬置元件性能参数即悬置刚度使系统各阶模态下的能量解耦率尽可能接近100%［6］。

2 悬置系统模态分析及隔振性能评估

2.1 动力总成悬置系统模态分析

笔者对上述的动力总成悬置系统模型进行模态分析，计算该模型的6 阶模态频率并提取相应的模态振型，由式(7)算得系统能量解耦率，可得该悬置系统的模态能量分布情况，如表4 所示。

表4 悬置系统模态频率和能量分布 %

2.2 动力总成悬置系统隔振性能评估

从能量解耦的角度来说，悬置系统各阶模态频率下，主自由度上的能量分布只有达到该频率下系统总能量的80%以上才能达到隔振要求［7］。

从表4 可以看到，该动力总成悬置系统除一阶模态下Ux方向上的解耦率达到82.17%外，其他模态下的主自由度上的解耦率都不太理想。对动力总成而言，其主要运动方向是Uz方向上的上下振动和绕x轴的转动，而该悬置系统在这两个方向上的能量分布分别只有72.18%和68.32%。因此，对悬置系统进行优化设计十分必要。

3 动力总成悬置系统优化设计

3.1 优化目标

以各阶模态频率下主自由度上能量解耦率ηi为优化目标，在相应频率下的优化目标函数为：

即使各阶模态频率下悬置系统主自由度上的能量分布大于总能量的80%。

3.2 约束条件

动力总成悬置系统的优化设计，其输入参数一般是悬置元件三向静刚度，或者是悬置元件在系统坐标系下的安装位置［8］。笔者所述动力总成悬置系统的优化设计，是在悬置元件布置形式大致确定的条件下进行的。选取悬置元件的刚度系数作为优化变量，由于作为优化对象的悬置系统采用左右对称布置形式，因此，优化变量共有6个。考虑到动力总成在整车设计时的布置及空间因素，设定优化约束条件如下［9］：

式中：x为优化变量，其集合为设计空间，表示前、后悬置元件三向刚度;f(x)为目标函数，是优化变量x的函数;η0i为悬置系统能量解耦率的最低期望值，笔者取80%;min(ηi)为悬置系统中各阶模态解耦率的最小值;fi为系统模态频率，笔者设定悬置系统相邻模态频率相差值不小于1 Hz;xL、xU分别为优化变量的上、下限取值范围，其值分别取悬置元件原始刚度值的1 ±30%。

3.3 优化结果

优化计算后各悬置元件三向静刚度如表5 所示。表6 为优化后悬置系统模态频率及系统能量分布。从表6 可以看到，优化后悬置系统模态频率得到了明显改善，不再出现相邻阶次模态频率过于接近的情况。x轴方向的能量解耦率达到90%以上，z轴方向上的解耦率从72.18%提高到85.3%，Rx方向上的解耦率也从68.32%提高到81.69%;优化效果达到预定要求。

表5 优化后前、后悬置各向静刚度 N/mm

表6 优化后悬置系统模态频率和能量分布 %

4 结论

笔者介绍了某矿用车动力总成及其橡胶悬置系统概况，从动力总成悬置系统能量解耦的角度出发，建立了ANSYS 软件下的系统简化模型，对所选用的悬置系统隔振性能进行了评价。以前、后悬置元件三向静刚度作为优化设计变量，设定若干优化条件，对该动力总成悬置系统进行了优化设计。计算结果表明，优化后悬置系统的各阶模态频率分布情况得到改善，相应频率下主自由度上的能量解耦率也大大提高，对该矿用车整车NVH 性能改善具有较大的参考价值。

［1］龙岩，史文库. 动力总成悬置系统优化方法的对比研究［J］.汽车工程，2011，33 (10)：875 -879.

［2］刘祖斌，刘英杰.发动机悬置设计中的动、静刚度参数研究［J］.汽车技术，2008(6)：78 -81.

［3］李勤，卢汉奎，陈树勋.关于发动机悬置系统分析的一种高效建模方法［J］.装备制造技术，2011(6)：48-49.

［4］赵建才，李堑，姚振强，等.车辆动力总成悬置系统的能量法解耦仿真分析［J］. 上海交通大学学报，2008，42(6)：878 -881.

［5］方锡邦，陈树勇，张文炬.轿车动力总成悬置系统隔振性能的仿真研究［J］.合肥工业大学学报：自然科学版，2003，26(2)：236 -241.

［6］徐燚，吴彰伟.基于ADAMS 的某客车动力总成悬置系统分析及优化［J］. 农业装备与车辆工程，2013，

51(4)：52 -57.

［7］柯有恩，刘志恩，颜伏伍.某微型车动力总成悬置系统隔振性能研究［J］.武汉理工大学学报：信息与管理工程版，2013，35(6)：846 -850.

［8］王天利，孙营，田永义.基于能量解耦法的汽车动力总成悬置系统优化［J］.机械设计与制造，2006(7)：31-33.

［9］龚曙光.ANSYS 参数化编程与命令手册［M］.北京：机械工业出版社，2009：100 -136.