压电发电系统负载特性研究

赵 燕，杨 隆，李天鹏

(武汉理工大学 机电工程学院，湖北 武汉430070)

目前在压电发电的材料研究、压电振子的结构行为和电能的存储电路等方面有了不少成果［1-3］，特别是对压电振子的结构模型进行研究以提高振子的发电效率方面和对能量收集电路的研究以提高能量利用率方面取得了一定的成就。但对于压电发电系统的负载特性研究很少，忽略了压电发电系统的负载特性对整个系统的影响。电路的负载特性是指当电路中加入不同的负载时，负载的性质、大小对整个电路参数，包括电压、电流和功率等的影响。笔者从压电发电系统的负载效应出发，研究负载的大小、性质对压电发电系统的影响，同时，通过实验证明压电发电装置在持续振动的条件下能够为低功耗的传感网供电。

1 压电发电系统负载特性研究

1.1 压电发电装置电路设计

压电发电装置主要包括压电振子、压电能量变换及存储电路，而压电发电系统不仅包含压电发电装置，还包括负载电路。已有研究集中在对压电装置的分析，而笔者将主要通过实验研究在负载分别为不同大小的电容、电阻时，负载两端电压的变化状况，并与理论分析进行比较。为保证压电发电装置的发电量能够有最大的输出，根据在固有频率时的压电振子发电最大的理论［4-6］，笔者采用共振法测得压电振子的固有频率为52 Hz。

在压电发电系统中，能量转换电路能够把振子的交流电压转变为直流电压，但是压电振子输出能量较少，不能持续为低功耗器件供电，需要将这些能量通过储能介质存储起来，用于持续地为负载供电。对比电解电容和锂离子电池，超级电容在能量密度、充电时间、充放电效率、充放电次数和工作温度范围等方面都有其优越性。笔者选用的超级电容容量有两种：0.1 F 和0.47 F［7-8］。压电发电系统负载特性实验框图如图1 所示。压电能量变换及存储电路如图2 所示。

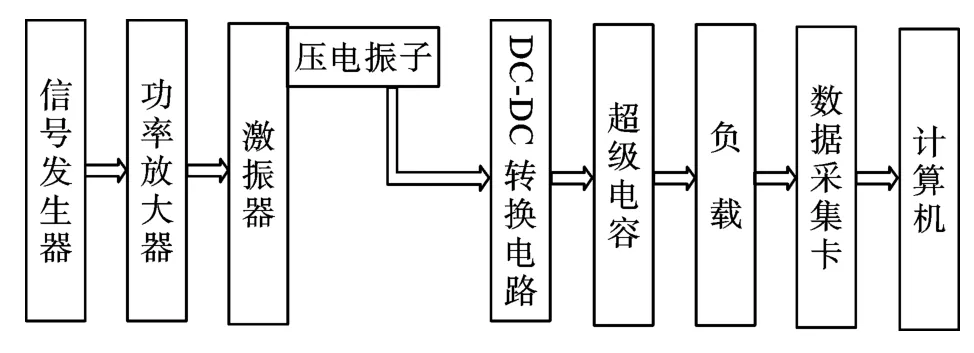
图1 压电系统负载特性实验框图

1.2 压电发电系统负载特性实验

通过调节信号发生器使其发出幅值恒为1V、频率恒为52 Hz 的正弦信号;同时，调节功率放大器使激振器输出力为0.2 sin(ωt)N，并在每个实验中保持持续振动。

(1)不外加负载。在不外加负载的情况下，开路电压波形界面图如图3 所示，压电振子开路峰峰值电压约为17.5 V。而经过DC/DC 电路后其直流输出电压约为3. 3 V。对超级电容(0.1 F)充电时，其两端电压状况如图4 所示。

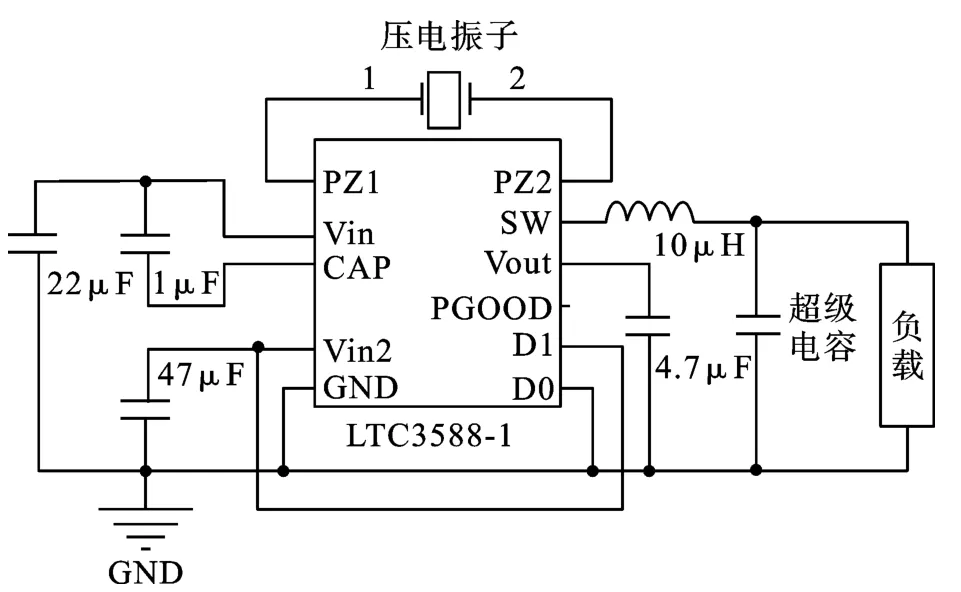
图2 压电能量变换及存储电路

图3 压电振子输出电压波形界面图

图4 充电时超级电容两端电压状况

(2)负载为电容。图5 描述了在负载为47 pF 和0.1 F 电容条件下，负载电压与时间之间的关系，其中，负载为pF、μF 和nF 数量级的电容时，充电曲线与47 pF 基本重合。

由图5 可知，在充电电容为0.1 F 超级电容，负载为pF 数量级的电容时，负载电容充满电的时间都大约为17 min;在负载电容等于储能超级电容时的充电过程与负载电容小于储能超级电容的充电过程有明显区别，并且充满时间变长，在负载为0.1 F 的电容时，超级电容充满电的时间达到35 min。

(3)负载为电阻。在10 kΩ，20 kΩ 和47 kΩ负载电阻下负载电压与时间之间的关系如图6 所示，其中，当负载电阻值大于47 kΩ 时，充电曲线与47 kΩ 基本重合。

图5 47 pF，0.1 F 负载电容下负载电压与时间之间的关系图

图6 10 kΩ，20 kΩ 和47 kΩ负载电阻下负载电压与时间之间的关系图

由图6 可知，在负载电阻大于等于47 kΩ 时，超级电容充满电的时间都大约为22 min，而负载电阻为20 kΩ 和10 kΩ 时，超级电容的充电状况与前面的负载电阻状况有明显不同，并且时间更长。负载电阻为20 kΩ 时，超级电容充满电的时间约为38 min，而负载电阻为10 kΩ 时，超级电容不能充满电，只是当负载两端的电压约为2.6 V时，整个压电发电系统进入动态平衡状态，最终负载两端的电压稳定在2.6 V;在负载电阻大于20 kΩ 时，超级储能电容都能够充满，达到最大的电压值3.3 V，而当负载电阻等于10 kΩ 时，电容两端的稳定电压值只有2.6 V，这是因为DC/DC 输出的功率值太小不足以满足电阻两端消耗的功率，使得最终的电压值只能在2.6 V［9-10］。

(4)负载为不同阻值下的输出功率。为说明负载在不同阻值下的输出功率情况，使压电振子的输出电压峰峰值为16 V，测量负载电阻两端的电压，通过公式P=U2/R，可得负载上的功率，通过数据处理得到输出功率与阻值的关系图如图7所示。当电阻由小变大时，输出功率开始不断增大，直到阻值为16 kΩ 时，输出功率达到最大值0.67 mW，此时的负载电阻与振子的阻抗基本相等，阻值继续增大，输出功率将减小。

图7 输出功率与电阻关系图

2 压电发电装置为传感网供电实验

笔者就压电发电装置能否对低功耗器件持续供电这一问题进行实验研究。采用两个ADT7410 温度传感器模拟传感网，实验原理框图如图8 所示，实验装置图如图9 所示。

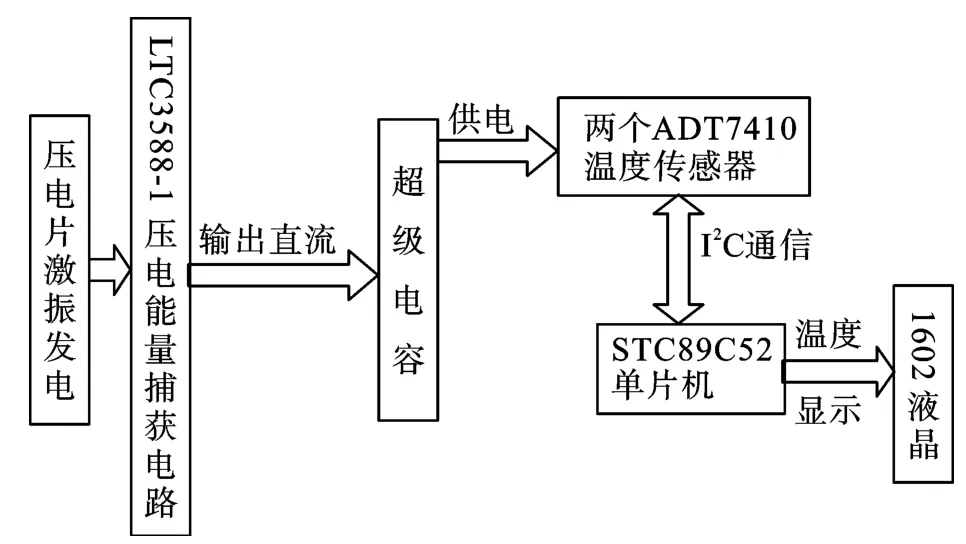
图8 实验原理框图

图9 实验装置图

(1)超级电容为两个ADT7410 器件供电实验。压电振子振动后得到的开路输出电压接上直流变换电路，把超级储能电容(0.47 F)充满电到3.3 V，充电过程大约为50 min。待超级电容充满电后为两个ADT7410 器件供电，超级电容两端电压变化状况如图10 所示。由图10 可知，超级电容可以为两个温度传感器正常供电，供电时间约为17 min。

图10 超级电容为两个温度传感器供电过程曲线图

(2)压电振子输出经整流后直接为两个ADT7410 器件供电。压电振子输出通过直流变换电路得到3.3 V 的直流电压，不通过超级电容，直接为两个ADT7410 器件供电，直流变换电路两端的电压输出波形界面图如图11 所示。当温度传感器采集温度时，电压有一个下降的过程，采集完成后电压又回到直流状态，此时，液晶显示屏能够准确显示温度，两个温度传感器正常工作。

图11 压电振子供电时整流输出电压波形界面图

(3)压电振子同时为超级电容充电和传感网供电压电振子输出经整流后得到3.3 V 直流电压，给超级电容(0. 47 F)充电，同时为两个ADT7410 温度传感器供电。超级电容端电压变化情况如图12 所示。由图12 可知，最终压电振子、超级电容和温度传感器负载三者处于动态平衡状态，电容两端的电压基本维持不变，两个温度传感器能够正常工作。

图12 压电振子同时为超级电容和两个温度传感器供电过程曲线图

3 结论

笔者针对压电发电系统的负载特性进行了研究，发现在不同电容值、电阻值的情况下，电路的负载特性会有明显不同;通过实验证明了持续振动的压电发电装置能对低功耗的传感网进行供电，并且可以通过对储能电路的设计来保证供电的持续性和稳定性。此外，对于实际应用中的大部分电路都可以简化为电容和电阻的串、并联连接，因此笔者的实验结果对复杂的负载电路也有一定的指导意义。

［1］阚君武，徐海龙，王淑云，等.多振子串联压电俘能器性能分析与测试［J］. 振动与冲击，2013，32(22)：79 -83.

［2］王浩金，邬丹燕，肖金，等.悬臂梁式压电发电结构理论模型及其仿真研究［J］. 机电工程，2011，28(11)：1412 -1415.

［3］阚君武，王淑云，彭少锋，等.多振子压电发电机的输出特 性［J］. 光学 精密 工程，2011，19 (9)：2108-2115.

［4］臧曦.压电装置的机电转换性能有限元分析［D］.武汉：武汉理工大学图书馆，2012.

［5］何学文，黄国平.基于ANSYS 的0-3 型压电振子的有限 元分析［J］. 压 电 与 声 光，2011，33 (6)：968-971.

［6］单小彪，袁江波，谢涛，等.不同截面形状悬臂梁双晶压电振子发电能力建模与实验研究［J］. 振动与冲击，2010，29(4)：177 -180.

［7］王永康，郑宗亚，闫雪奎.基于压电发电的同步电荷采集电路仿真［J］.机电信息，2012(3)：126 -127.

［8］JIANG S N，LI X F，GUO S H，et a1.Performance of a piezoelectric bimorph for scavenging vibration energy［J］.Smart Mater Struct，2005，14(2)：769 -774.

［9］王磊.多谐振频率压电振动能量回收结构特性及实验研究［D］. 北京：北京交通大学图书馆，2010.

［10］曾平，佟刚，程光明，等.压电发电能量存储方法的初步研究［J］.压电与声光，2008，30(2)：230-235.