关注本质:“小研究学习”的应然追求
周卫东
[摘 要]“平均数”的教学应让学生学习哪些本质?平均数是数据的代表,反映的是一组数据的集中趋势,平均数常用于统计对象的一般水平,它既可以反映出一组数量的一般情况,也可以用来进行不同组数量的比较,以看出组与组之间的差别。求平均数是分析数据的一种重要方法,在日常生活中,特别是工农业生产中经常要用到,如平均成绩、平均身高、平均产量、平均速度等。教学中应如何把握这些学科本质?可以“小研究学习”的方式,让学生在研究、交流、反思中自然领悟和把握。
[关键词]平均数 移多补少 易变性
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)14-014
A.课前学生进行前置性小研究。(研究单详见前文附录)
B.课堂学习与交流过程
一、小组交流,分享各自研究成果
师:这节课,我们学习一个新的数学知识,大家知道是什么吗?
师:关于“平均数”的知识,课前我们已经做了一个小研究,请大家拿出来,4人小组相互交流一下,在交流中如果遇到不一样的想法,可以商量商量,再做适当的修改。开始吧!”(时间5分钟左右)
二、全班交流
1.感受平均数的意义,掌握平均数的求法
师:哪个小组愿意与大家分享自己的研究成果?
生1:下面由我们小组来与大家交流。我先汇报我的想法。我觉得C组应该是冠军,因为C组的平均数最大。我算了一下,A组的平均数是4个,用(3+8+1)÷3=4(个);B组的平均数也是4个,用(3+5+4+4)÷4=4(个);C组的平均数是5个,用(4+5+6)÷3=5(个)。
生2:我不同意生1的想法,我觉得A组应该是冠军,因为他们说得对,最大数8在他们组啊!
(这时,班上大多数学生都举起了手)
生3:最大数在他们组,可是最小数1也在他们组啊!所以不能看单个人的数量,而要看整个组的水平!
生4:对,不能看某个人的数量,因为他不代表整个组的水平。
生5:同样,B组的说法也不对,虽然他们小组的总数最多,但他们小组的人数最多,平均摊到每个人的头上只有4个,而C组摊到每个人的头上是5个。所以我同意C组是冠军。
师:这个“摊”字挺有意思!摊字还可以怎么解释?
生6:摊就是平均的意思,平均就是让每个人都一样多!
师:多形象的一个字啊!让我们对一个科学的概念得到很好的理解,谢谢你!
师:孩子们,我们来把刚才大家的发言整理一下。A、B、C组都想用一个数据来代表自己组的水平(板书:数据代表),回忆一下,三个组的数据代表分别是什么?
生7:A组的代表是最大数,B组的代表是总数,C组的代表是平均数。
师:没错,在不同的场合下,最大数、总数和平均数都可以作为一组数据的代表,那在这种情况下,谁做数据代表更合适呢?
生:平均数。
师:平均数反映了一组数据的集中趋势,代表了这组数据的整体水平。
师:刚才生1同学介绍了求平均数的方法,谁来概括一下,她是怎么求平均数的?
生8:先求总数,再除以个数。
师:大家同意吗?(板书:平均数=总数÷个数)
生9:我来补充,求平均数还可以这样想,比如C组,把王宇的6个,移一个给李小钢,这样,3个人就都是5个了,那么平均数就是5了。
师:你是一个很善于思考、善于观察的孩子!那生9的这种方法,谁来给它取一个名字?
生10:取大给小。
生11:移多补少。
师:真好!这两个名称意义都表达了同一个意思。数学上规范的名称叫“移多补少”!
2.灵活运用平均数的求法,进一步感受平均数的“易变性”
师:小研究的第2题,哪个小组愿意与大家交流?
生12:下面由我们小组来与大家交流。我认为D组可能得冠军,也可能得不到。
生13:对,我来补充,刚才C组是冠军,平均数是5个,现在D组4个人来投,总数要达到20个,平均数才正好是5个,现在前3个人的总数是6+5+3=14个,14个与20个相差6个,第4个人如果投6个,平均数就是5个,正好与C组并列冠军,要想得绝对冠军,平均数就必须超过5个,那第4个人至少要投7个。
生14:对,我来小结一下,这里有3种情况。如果第4个人投了6个,平均数就正是5个,与C组是并列冠军;如果小于6个,平均数小于5个,就得不到冠军;如果大于6个,平均数大于5个,就是绝对冠军。
师:噢,听了这个小组的发言,大家有没有感觉到,左右D组能不能得冠军的个数只是区区的1个,多1个与少1个,结果完全不一样,看来平均数是易变的,难怪有人这样形容平均数“平均数这东西很敏感,任何一个数据的风吹草动,都会使平均数发生变化”。现在看来,这话有道理吗?
3.进一步理解平均数“介于大数与小数之间”等特性
师:孩子们,让我们一起来交流第3题,相信大家对平均数的认识会更深一层。
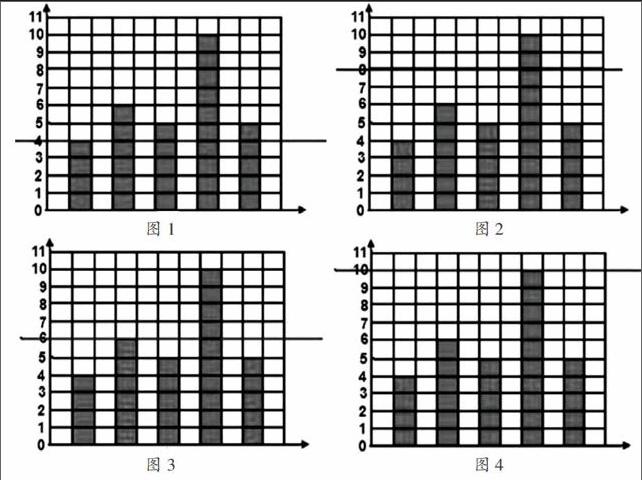
生15:我认为图3是对的。因为图1的虚线取的是最小数,平均数不可能是最小数,图4的虚线取的是最大数,平均数也不可能是最大数,图2多的部分拿给少的部分不够分,所以我觉得是图3是对的。
生16:我同意生15的想法。我根据5个人的多少,分别假设了他们投球的个数,用具体的数算一下就知道了。
师:大家同意吗?其实,生16介绍的这种方法,老师预先也准备了,大家一起来感受一下。
师:用图中的具体数据计算一下,哪一幅图是正确的呢?
师:通过对这道题的研究,你对平均数又有哪些新的认识呢?
生17:平均数大于最小数,小于最大数。
生18:平均数介于最大数和最小数之间。
生19:平均数是个中间数。
4.进一步理解“平均数是一组数据的集中趋势,个别数值不能代表整体水平”等特性
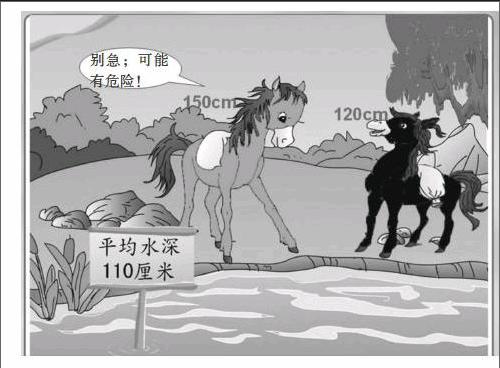
师:你觉得黑马说得有道理吗?(学生交流略)
师:孩子们,这个故事还没有结束呢。请看续节——
师:你觉得黄马说得有道理吗?(学生交流略)
师:听了这个故事,你觉得有哪些收获要与大家分享呢?
【课后反思】
“小研究学习”的课堂,不仅要关注学生的学,更应关注学科特质的提炼与表达,要让学科的本质占领课堂的主阵地,要体现出浓浓的“数学味”。
就平均数而言,“数学味”体现在重在突显概念的本质。
置于整体,概念的特点更能显现。众所周知,同样看一个事物,从局部看局部,从整体看局部,后者显然更为清楚。而在数学学习的过程中,也有同样的道理。平均数是什么呢?我们需要一个全景式的了解,统计学认为,描述一组数据的特征量有三种:差异量,集中量和相关量。集中量就是表示一组数据的典型水平或集中趋势的量。集中量又分为众数,中位数与平均数。平均数又分为加权平均数,调和平均数和算术平均数。从现实情况看,小学生学习的平均数更多的是指算术平均数,较复杂的平均数中有加权平均数。有一个这样整体系统的认识,教学中更能抓住其本质特征。从这些背景知识中,可以发现:平均数是众多集中量(小学生讲“代表数”比较容易理解)中的一个,并不唯一。反思第一环节,在学生判断哪一组得冠军的环节,要找一个能代表小组意见的分数时,从学生的回答中,我们可以看到除了平均数还有总数和最大数的影响,这就是一个概念形成的真实的整体背景。
丰富经历,概念的形成更加完整。平均数是一种反映一组数据集中趋势的统计量,是描述数据的重要统计指标之一,理解平均数的统计意义是教学的关键,有经历,才会有体验。纵观全课,四个教学场景各有侧重,将学生置于全方位的“场域”之中。引导学生通过辨析讨论,体会“平均数肯定在最大数与最小数之间”“平均数有时会受到极端数据的影响”“平均数是一个特征数,并不是所有数都是这个数”等特点,进一步理解平均数的实际意义,这样的教学,有助于学生今后理解用平均数表示的数据的特征,并且在进行数据分析时能想到用平均数刻画数据。
加强联系,概念的价值更为丰实。数学联系,就本节课教学设计而言,主要指数学与其他学科的联系,以及数学与德育的联系。本节课上,在数学学习的过程中,要丰富数学学习的素材,让数学与德育的联系并非只是停留在形式。在课堂上,当听完新“小马过河”的故事时,学生不仅对黄马和黑马赋予了人的个性特点,同时联想现实生活中的一些“平均数”,如重点中学的学生平均分数比一般学校高,那么是否就是就读重点中学好;好的单位平均工资比一般单位好,那么是否要选择好单位就业,以及“宁当鸡头不作凤尾”的俗语,都是对学生的学习和生活有着长远的教育意义的。“作为教育任务的数学”承载的不只是数学的学习。虽然我们也反对“去数学化”,反对数学与其他学科的牵强联系,也不赞成“贴标签式的德育渗透”,但我们认同和倡导用儿童所能接受并喜欢接受的方式,加强联系,渗透德育,真正实现“数学教学,不只教学数学。”
(责编 金 铃)

