考虑波浪作用下的深水桥墩地震响应分析

林曾，袁万城

(同济大学土木工程防灾国家重点实验室，上海 200092)

考虑波浪作用下的深水桥墩地震响应分析

林曾，袁万城

(同济大学土木工程防灾国家重点实验室，上海 200092)

跨海深水桥梁会受到地震和波浪的共同作用，研究地震和波浪共同作用下的深水桥梁动力响应问题具有非常重要的意义，并且该问题一直没有得到很好解决。本文以某典型深水桥墩为例，研究波浪作用对深水桥墩地震响应的影响。首先建立了考虑波浪作用下的深水桥墩地震响应分析方法，然后针对仅地震作用、仅波浪作用、同时考虑波浪作用下的地震作用3种情况对该桥墩进行动力响应分析。分析结果表明，动水压力增大了深水桥墩的地震响应，其影响程度与输入地震波的频谱特性有关;波浪响应值比地震响应值小;但考虑波浪作用前后的桥墩地震响应值变化较大，考虑地震作用下的深水桥墩地震响应不是两者独立作用下动力响应简单的叠加。

深水桥墩;地震响应;波浪作用;Morison方程;动水压力

随着全球经济的不断发展，世界各国都在加快交通基础设施的建设，桥梁作为交通运输的枢纽，在朝着大跨度发展的同时，也涌现了越来越多的跨海深水大桥，如希腊Rion-Antirion大桥、日本明石海峡大桥、意大利墨西拿海峡大桥。同时，我国也正在建设沿海高等级公路，包括五个大型跨海工程项目，从南到北依次跨越渤海海峡、长江口、杭州湾、珠江口伶仃洋和琼州海峡，这些水域的水深非常大，一般在80 m左右。跨海深水桥梁在施工和运营期间面临着极其复杂的环境条件［1］，如地震、波浪、海风、水流等情况。因此，跨海深水桥墩除了承受自身重力和上部活载作用外，还要承受地震力、波浪力、风力等环境荷载。通常情况下，地震发生时跨海深水桥梁会受到地震和波浪荷载的共同作用，故此类桥梁在考虑波浪作用下的抗震设计研究亟待深入开展。

国内外学者针对地震与波浪共同作用下水中结构的动力响应问题进行了一系列研究，并取得了相应的成果。Penzien等［2］采用随机振动方法研究了海浪和强震共同作用下，底端固定的近海塔架平台安全性;Yamada和Kawano等［3］以Bretscheider波功率谱模拟波浪，Kanai功率谱模拟强震输入，采用随机振动方法分析了海洋结构的动力反应;Karadeniz［4］采用谱分析方法，视波浪和地震为随机过程，分析了三维结构在地震和深水波浪耦合作用下的动力反应;何晓宇和李宏男［5］对导管架平台在地震作用和地震与波浪共同作用两种工况下进行了研究，分析中考虑了地震设防烈度、风浪条件及场地土类型等因素;李忠献、黄信［6］以一座3跨深水连续梁桥为例分析了地震和波浪联合作用下深水桥梁的动力响应。在海洋工程、水利工程等领域这方面的研究比较成熟，然而在桥梁工程领域这方面的研究非常少，很多学者都是将深水桥梁地震响应问题和波浪对结构作用问题独立考虑［1，10］，即有关考虑波浪作用下的深水桥梁地震响应的研究屈指可数。

鉴于此，本文建立考虑波浪作用下的深水桥墩地震响应分析方法，以一个典型圆柱型实体桥墩为例，利用有限元程序针对3种情况(仅地震作用、仅波浪作用、考虑波浪作用下的地震响应)分别对桥墩进行动力响应分析，以便分析波浪作用对深水桥墩地震响应的影响。

1 考虑波浪作用下的深水桥墩地震响应分析方法

1.1 地震动水压力及波浪力求解

深水桥墩结构所受到的波浪力求解方法与结构横向尺度大小有关［8］，对于横向尺度较小(d/L＜0.2)的结构，结构物的存在对波浪运动无显著的影响，此时可采用Morison方程法求解波浪力;对于横向尺度较大(d/L＞0.2)的结构，结构本身的存在对波浪运动有显著的影响，对波浪的绕射效应必须加以考虑，此时可采用绕射理论法或弗汝德-克雷洛夫(Froude-Krylov)法求解波浪力，其中d为桥墩直径，L为波浪波长。

对于d/L＜0.2的横向小尺度桥墩结构，深水桥墩波浪力的相关研究主要采用1950年Morison等［9］提出的半经验半解析Morison方程，忽略了结构对水运动的影响，认为水对结构的作用分别由未受扰动的加速度场和速度场引起的沿水运动作用于结构上的惯性力和阻力造成的，波浪对单位长度柱体上的波浪力fH为:

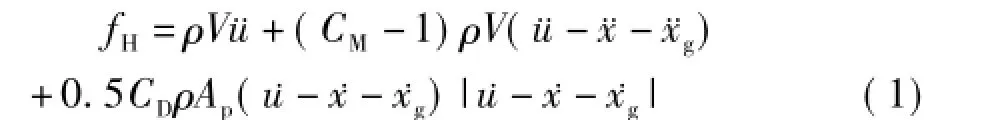
式中:ρ为水的密度;V为单位长度柱体的体积;Ap为单位长度柱体垂直于水流方向的投影面积;、分别为水的绝对加速度和绝对速度;、分别为桥墩的相对加速度和相对速度;g、g分别为地震动加速度和速度;CM为惯性力系数;CD为拖曳力系数。

当地震单独作用时，深水桥墩结构会受到地震动水压力的影响，用附加质量考虑地震动水压力对桥墩的作用。可假设水是静止的，相当于==D，经过一系列推导(由于论文篇幅所限，详细求解过程方法参见文献［7］)，最后假设结构两相邻单元中点之间水与结构的相对速度不变，且作用在结构第i个节点的作用力为与i点相连的各个构件受力总和的一半，即每个节点只承受单元受力的一半，则节点i处水的等效质量为［6］:

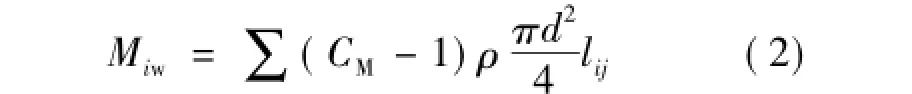
式中:j为与节点i相邻的节点;lij为第ij单元有效长度的一半;d为圆柱体结构直径;一般情况下对于圆柱体结构，CM=2.0。

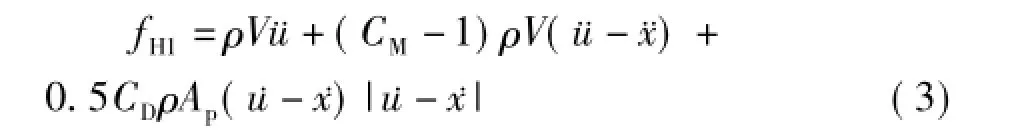
当地震和波浪同时作用时，此时单位长度柱体上的波浪力fH2如式(1)所示。

1.2 运动方程建立

当地震单独作用时，深水桥墩结构会受到地震动水压力的影响，此时桥墩结构的运动方程为:

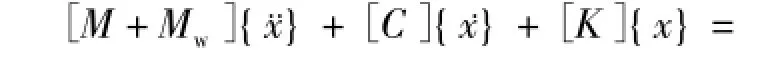
式中:［M］为桥墩结构的质量矩阵;［Mw］为动水压力的附加质量矩阵;［C］为桥墩结构的阻尼矩阵;［K］为桥墩结构的刚度矩阵;{}、{}、{x}分别为桥墩结构各节点的加速度、速度和位移向量; {g}为地震动加速度向量。

当波浪单独作用时，此时桥墩结构的运动方程为:

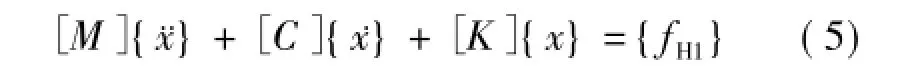
当考虑波浪作用下的深水桥墩结构地震响应的运动方程为:

式(5)、(6)中，{fH1}、{fH2}均为相应的波浪力向量，其余字母含义同前。

桥墩结构的阻尼矩阵［C］采用瑞利阻尼，运动方程的求解采用Newmark时间积分法。

2 深水桥墩计算模型的建立

本文以某典型圆柱型实体桥墩［7］为例，该桥墩的截面直径d=5 m，墩高H=24.7 m，水深h= 20 m，墩上为预应力混凝土主梁，梁的计算跨度L0=51.1 m，计算高度为H0=4.25 m，质量密度ρ =2500 kg/m3，弹性模量E=3.0×104MPa，计算时考虑桥面质量，并取一跨梁桥系质量，大小约为m=525000 kg，将其以集中质量的形式作用在桥墩顶部。利用有限元程序进行数值计算，建立桥墩的有限元模型时，仅考虑其在平面内的振动，墩底完全约束，刚性固结，简化的桥墩及模型如图1所示。

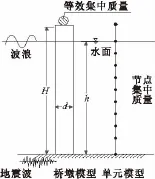
图1 简化桥墩及其模型

3 深水桥墩的动力响应分析

3.1 深水桥墩的地震响应分析

在Morison方程的基础上，用附加质量考虑地震动水压力作用对深水桥墩进行地震响应分析。地震设计烈度为8度，输入地震波为幅值按比例经过调整的1995年Kobe地震波和1940年El Centro地震波水平南－北分量，地震动的加速度峰值(PGA)为0.2g，其加速度时程曲线见图2、图3所示。为了分析地震动水压力对深水桥墩的影响，同时计算了无水情况下的桥墩地震响应。

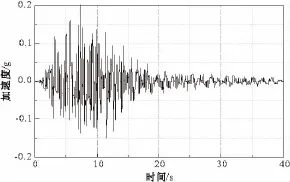
图2 Kobe波加速度时程

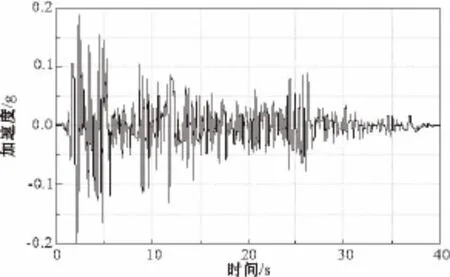
图3 El Centro波加速度时程

地震作用下桥墩的动力响应幅值见表1所示，表中仅列出了桥墩墩顶和墩底地震响应幅值。由于篇幅所限，仅给出Kobe地震波作用下墩底内力的时程图，见图4所示。

表1 桥墩的地震响应幅值

为了更好衡量动水压力对深水桥墩地震响应的影响，此处引入动水影响系数ts，其定义:

式中:s代表桥墩墩顶的水平位移、墩底的剪力和弯矩幅值。

地震作用下深水桥墩墩顶水平位移、墩底内力的动水影响系数ts见表2所示。

图4 Kobe波作用下桥墩底的内力时程

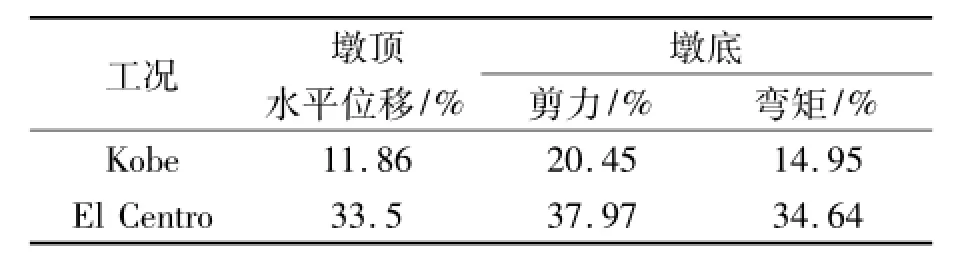
表2 深水桥墩的地震动水影响系数ts

由图4可以得到，地震动水压力对深水桥墩结构地震响应有显著的影响，其增大了桥墩墩底的剪力和弯矩。

由表1、2可以得到，考虑地震动水压力后，深水桥墩墩顶水平位移、墩底剪力和墩底弯矩均有不同程度的增加。Kobe波和El Centro波分别作用下，桥墩的地震动水影响系数不同，说明动水压力对其影响程度与地震波的频谱特性有关。

3.2 深水桥墩的波浪响应分析

根据桥址处水域的常年水文观测资料，深水桥墩所在处的设计波参数:波浪周期T=6 s，有效波高H1=3.4 m，如下图5所示。

图5 波浪示意

对于有限水深(0.05＜h/L＜0.5)，周期T与波数n、波长L的关系如下式［8］:

式中:h为水深。

由周期根据公式(8)、(9)可得波长L=55 m，此时墩的横向尺寸与波长之比d/L=5/55= 0.09＜0.2，该墩属于横向小尺寸结构，可采用Morison方程考虑波浪力作用，其中波浪采用Stokes五阶波浪理论，CD、CM的取值应与所采用的波浪理论有关。根据挪威船检局(1974)规范中规定［11］，此处的CD=1.0，CM=2.0。

波浪作用下深水桥墩的动力响应幅值见表3所示，图6给出波浪作用下深水桥墩墩底内力时程图。

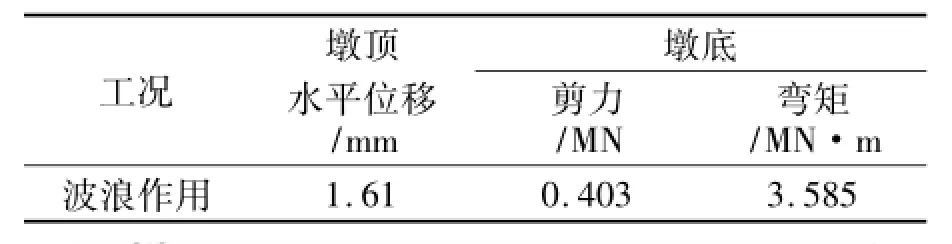
表3 深水桥墩的波浪响应幅值

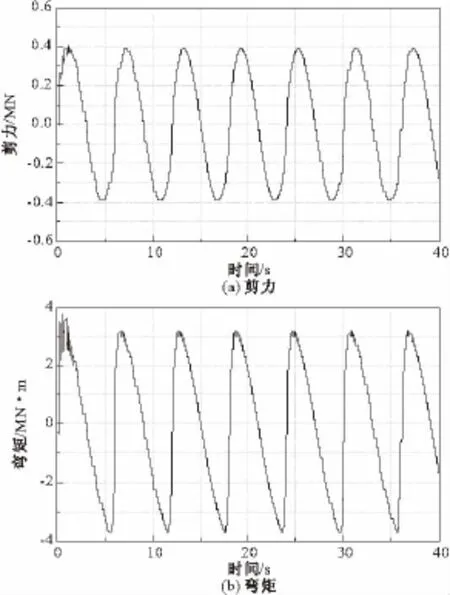
图6 波浪作用下桥墩底的内力时程

由表3可以得到，波浪作用下深水桥墩墩顶水平位移、墩底剪力和墩底弯矩分别为1.61 mm，0.403 MN和3.585 MN·m。与地震响应(见表1)相比，深水桥墩的波浪响应较小。

由图6可以得到，桥墩波浪响应值随时间呈类似正弦曲线规律变化，频率为0.167 HZ，与输入波浪的频率相吻合。同时图6与图4对比，进一步表明深水桥梁波浪响应值比地震响应值小。

3.3 考虑波浪作用下的深水桥墩地震响应分析

深水桥墩在地震作用下同时会受到波浪的作用，考虑波浪作用对深水桥墩进行地震响应分析。此处假设地震和波浪沿着同一方向作用。

考虑波浪作用下的深水桥墩地震响应幅值见表4所示。由于篇幅所限，仅给出Kobe地震波在考虑波浪作用下的墩底内力时程图，见图7所示。

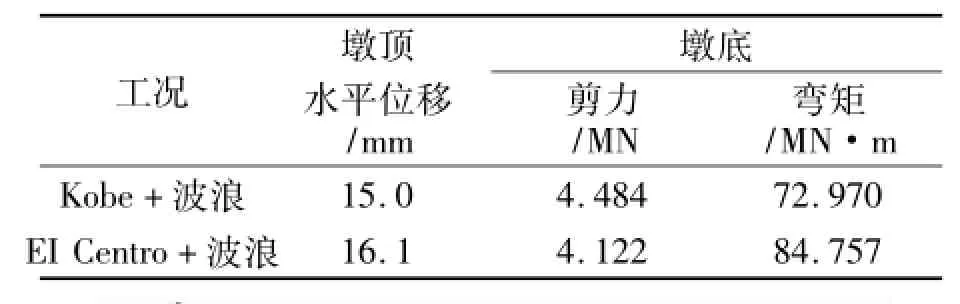
表4 考虑波浪作用下深水桥墩的地震响应幅值

图7 Kobe波对应的桥墩底内力时程

表4与表1对比，发现深水桥墩在考虑波浪作用后的地震响应幅值减小，并且其幅值不是深水桥墩地震响应幅值与波浪响应幅值简单的叠加。更需注意的是，考虑波浪作用的桥墩地震响应幅值与仅考虑地震作用的响应幅值之差大于波浪响应幅值。另外，El Centro地震波也有相同的规律。

由图7可以得到，考虑波浪作用下的深水桥墩地震响应时程曲线与仅地震作用下桥墩动力响应时程曲线差别较大，进一步表明考虑波浪作用下桥墩地震响应值并不是地震和波浪独立作用桥墩动力响应值简单的叠加，地震和波浪同时对深水桥墩的作用过程十分复杂，其原因可能主要有三点，一是地震、波浪存在相位差，导致两者独立作用深水桥梁动力响应峰值不是在同一时刻出现，二是地震波的频谱特性与波浪的频谱特性相差较大，三是两者施加在桥墩的不同位置，其中地震荷载施加在桥墩底部，而波浪荷载施加在近水面的墩身上，并且波浪对桥墩的自振特性有影响。

4 结论

(1)地震动水压力对深水桥墩结构地震响应有显著影响，其增大了桥墩的动力响应。动水压力对其影响程度与输入地震波的频谱特性有关。

(2)与地震响应相比，深水桥墩的波浪响应较小，其频率与输入波浪的频率相吻合。

(3)考虑波浪作用前后的深水桥墩地震响应变化较大，其差值大于仅波浪作用时的动力响应值，考虑波浪作用下的动力响应幅值不是两者独立作用下的动力响应幅值的简单叠加。

［1］赖伟.地震和波浪作用下深水桥梁的动力响应研究［D］.上海:同济大学，2004.

［2］Penzien J，Kaul M K.Response of offshore towers to strongmotion earthquakes［J］.Earthquake Engineering＆Structural Dynamic，1972，1(1):55-68.

［3］Yamada Y，Kawano K，Iemura H，et al.Wave and earthquake response of offshore structures with soilstructure interaction［J］.Proceeding of JSCE，Structure Eng/Earthquake Eng，1988，5(2):157-166.

［4］Karadeniz H.Spectral Analysis of Offshore Structures under Combined Wave Earthquake Loadings［C］// The Ninth International Offshore and Polar Engineering Conference.Brest:Lnternational Society of Offshore and Polar Engineers，1999:504-511.

［5］何晓宇，李宏男.地震与波浪联合作用下海洋平台动力特性分析［J］.海洋工程，2007，25(3):18-25.

［6］李忠献，黄信.地震和波浪联合作用下深水桥梁的动力响应［J］.土木工程学报，2012，45(11): 134-140.

［7］高学奎，朱晞.地震动水压力对深水桥墩的影响［J］.北京交通大学学报，2006，20(1):55-58.

［8］竺艳蓉.海洋工程波浪力学［M］.天津:天津大学出版社，1991.

［9］Morison JR，O’Brien M P，Johnson JW，etal.The force exerted by surface waves on piles［J］.Petroleum Transactions，AIME，1950，189:149-154.

［10］伍勇吉，魏凯，庞于涛，等.不同水深环境下桥梁群桩基础动力特性［J］.土木工程与管理学报，2012，29(2):21-25.

［11］张洁.动水压力对深水高墩桥梁地震响应影响的分析［D］.重庆:重庆交通大学，2012.

Seism ic Response of Bridge Pier in Deep Water Considering W ave Action

LIN Zeng，YUANWan-cheng
(State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai200092，China)

Earthquake and wave action may be applied to bridges crossing sea in deep water at the same time，it is very important to analyze the dynamic responses of bridges in deep water under earthquake and wave action，besides，this problem is not well solved.Taking a common bridge pier in deep water as an example，the wave action effect on the seismic response of this pier is investigated.The analysis method of the seismic response of this pier considering wave action is established.The dynamic response analyses of this pier under 3 working conditions that contain the earthquake action only，wave action only and earthquake action considering wave action are then conducted.Themajor conclusions are that，the dynamic responses of bridge pier in deep water are increased because of earthquake induced hydrodynamic pressure，and the influence of hydrodynamic pressure is related to the spectral characteristics of earthquake waves.Compared to the seismic response value，the wave action response value of this pier is very small.But the seismic response difference between considering wave action and not considering is very big.Seismic responses of bridge in deep water considering wave action can not be obtained by combining seismic response and wave action dynamic response by superposition.

bridge pier in deep water;seismic response;wave action;Morison equation;hydrodynamic pressure

U442.5+5

A

2095-0985(2015)02-0037-05

2014-12-28

2015-03-01

林曾(1989-)，男，江西萍乡人，硕士研究生，研究方向为桥梁抗震(Email:13linzengjx@tongji.edu.cn)

国家自然科学基金(51278376;51478339);土木工程防灾国家重点实验室基金(SLDRCE14-B-14)