Davidenkov土动力非线性模型在OpenSees软件中的实现与应用
赵旭清
(中铁十六局集团有限公司,北京 100018)
Davidenkov土动力非线性模型在OpenSees软件中的实现与应用
赵旭清
(中铁十六局集团有限公司,北京 100018)
在地下空间被大规模开发的过程中,地下结构抗震问题逐渐得到重视,由于地下结构的特殊性,对于地下结构周围地基土动力性质的研究显得尤为重要。土在动荷载作用下会出现非线性、滞后性和变形累积性等力学特性,骨架曲线可以通过实测资料采用函数进行拟合的方式确定。本文以武汉地区软土为研究对象,通过共振柱试验得到不同围压下剪应变和剪切模量的关系,并拟合出Davidenkov模型中的参数。以OpenSees地震工程模拟开放体系为平台进行二次开发,编制Davidenkov模型材料子程序,并对该黏土在地震作用下的动力响应进行了分析,同时对比试验结果验证了程序的可靠性。
Davidenkov模型;共振柱试验;OpenSees;地震动力响应
土在动荷载作用下会出现非线性、滞后性和变形累积的力学特性,其中非线性体现在骨架曲线的非线性中,骨架曲线可以通过实测资料采用函数进行拟合的方式确定,常用的拟合函数有直线、双曲线、Ramberg-Osgood曲线等[1];滞后性特征一般通过滞回曲线的形状来表征,而土体的变形累积特性一般通过滞回圈中心的移动来表征。在进行有关于土在循环荷载作用下力学行为研究的过程中,最困难的是确定描述土体性质的相关参数,因此,在进行有关于岩土工程的抗震设计时,采用动剪切模量、阻尼比等参数精确的描述土体的动力特性是需要解决的关键问题。
1 Davidenkov模型基本理论
Davidenkov模型是由Hardin[2]等提出的一种黏弹性模型,基本思想是采用某种双曲线函数来模拟土体应力–应变的骨架曲线,其动剪切模量之比可用如下表达式表示:

式中:G为剪切模量;Gmax为加载初始的最大剪切模量;γ为剪应变值;γref为参考剪应变值。
参考剪应变的取值可根据G/Gmax为0.5时的剪应变值确定,如图1所示。此时Hardin型骨架曲线方程可以表示为如下形式:
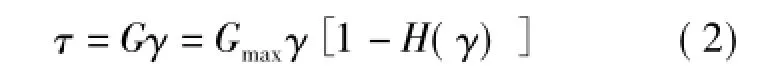
式中:τ为剪应力;H(γ)为表示曲线基本形状的函数。

图1 应力、应变与参考剪应变关系
Gmax应根据共振柱试验确定,但在没有试验的情况下,也可以通过Hardin提出的适用于未受扰动黏性土和砂土的经验公式来确定:
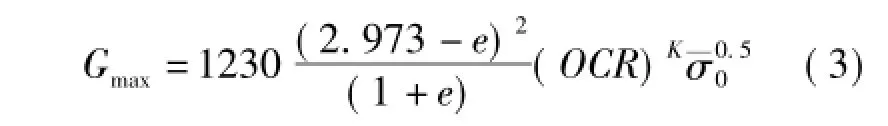

表1 K取值
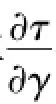
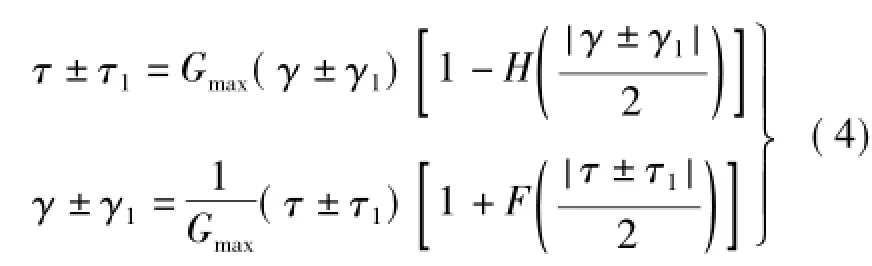
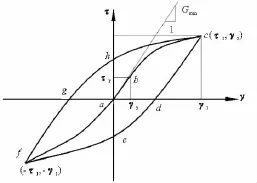
图2 Mashing法则示意
Martin和Seed(1982)等[4]对Hardin双曲线模型进行修正,采用Davidenkov型骨架曲线对上述应力–应变关系进行描述,上式中的H(γ)被改为:

式中:A,B为由土体性质决定的拟合参数;γ0为剪应变幅。
当A=1,B=0.5,γ=γr(γr为参考剪应变幅)时,该模型的骨架曲线即为Mashing骨架曲线表达式[6]:

将式(6)代入式(5)可得到Davidenkov模型加载再卸载曲线表达式:
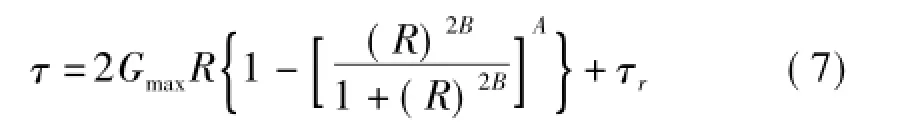
式中:R=(γ-γr)/(2γ0);τr为参考剪应力幅。
由于τ是关于γ的函数,因此将式(7)对于γ求导可得骨架曲线中G的增量表达式:

将式(6)对γ求导可得滞回曲线中G的增量表示形式:
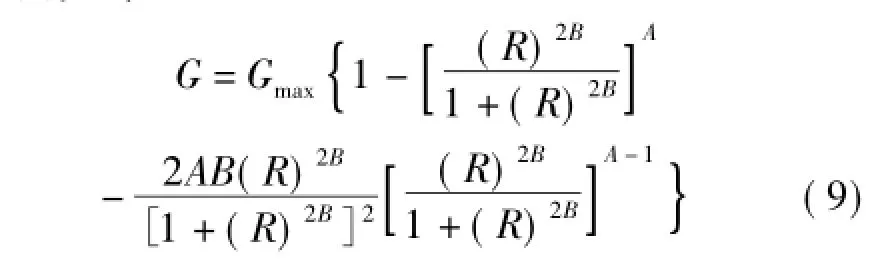
2 OpenSees程序框架
OpenSees作为开源有限元分析软件,不仅仅代码公开透明,并且OpenSees提供了良好的接口可供使用者方便的进行二次开发,使用者可以在不需要了解OpenSees完整框架结构的情况下,在所需要的方面对程序进行改进,增加用户自定义的材料、单元等内容。同其它面向对象程序设计的软件框架相同,OpenSees也具有抽象、封装、继承以及多态的性质[7]。
OpenSees在PEER等研究机构及国内外高校中的一些科研项目中已被广泛应用于结构及岩土工程的抗震分析,例如国家自然科学基金中美合作项目——重大工程地震灾变模拟系统OpenS-ees的联合开发与应用,其目标是将OpenSees作为重大工程地震灾变的主要模拟平台之一。
根据文中所阐述的Davidenkov本构模型的基本理论,程序计算流程图如图3所示,程序编制的主要思路如下:首先对于自定义材料中的相关参数进行初始化,随后提取从element传入的应变值,对其是否为拐点进行判断,如果经判断该点为拐点,则将拐点信息存储到相应的数组中进行保存,若不是拐点还需对其是否超过最大剪应变进行判断,若超过最大剪应变则将剪应变更新为最大剪应变,否则通过式8、9进行剪切模量的更新。在对剪切模量更新完成后,调用getstress()函数对应力值进行更新,最后进行收敛性判断,OpenSees中提供的收敛性判断有力平衡、位移平衡及能量守恒三种基本的判定方法可供选择,可根据情况进行设定,如果不收敛则重新进行一遍上述步骤直至在给定的精度和迭代次数的范围内计算收敛为止。

图3 程序计算流程
在本程序编制过程中拐点的判断是十分关键的问题。对于拐点的判断可以通过在程序中设置两个数组,分别用来存储近几次的应变值和历史拐点信息,每进行一次循环,都会将存储进几次应变值信息的数组中信息进行更新,通过判断应变增量的方向即可判断出该点是否为拐点,即可将此次的拐点信息存入对应的变量中用于程序后续的调用。
3 程序验证及参数分析
本文进行程序验证的方法如下,取一个单元,将单元材料属性赋予为自编材料属性,根据模拟土体的需要,单元类型选取为四边形单元,单元尺寸定为1 m×1 m计算时对单元施加正弦形式的动力荷载,加载总时间为10 s,最大振幅控制在20 mm,假设土体存在残余强度且破坏时剪切模量最小值取为0.05Gmax。通过这种方式得出单元在动力加载时的应力、应变规律以验证程序的正确性。由于试样较多且每个试样根据围压的不同又分为三种情况,为了方便起见,选取一个可塑粉质黏土试样进行验证分析。
3.1 可塑粉质黏土程序验证
图4分别给出了围压100 kPa情况下单元底部和顶部的加速度时程曲线和位移时程曲线,从图中可以看出,顶部和底部的加速度时程曲线和位移时程曲线均存在一个相位差,并且单元底部和顶部加速度峰值和位移峰值均存在较小差值,其中底部与顶部加速度峰值最大相差16.18%,位移峰值最大相差4.07%。同时可以看出,程序编制过程中的关键问题——拐点判断的方法有效。
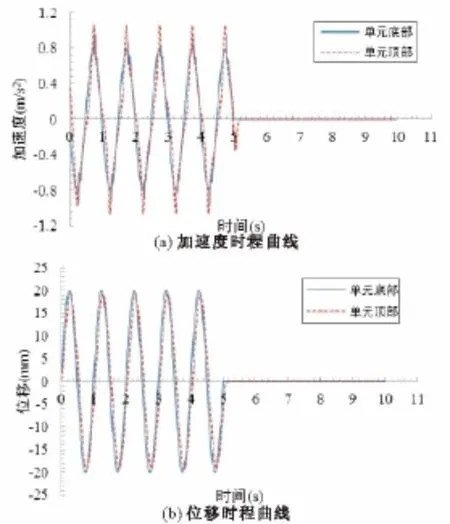
图4 围压100 kPa时加速度及位移时程曲线
图5、图6分别为围压在450 kPa、700 kPa时归一化剪切模量与剪应变关系曲线。从图中可以看出,程序计算结果与试验结果依旧趋势相同且吻合程度较好,由此可验证在可塑粉质黏土的动力分析中,所编制的程序是有效的。
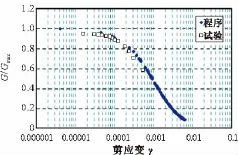
图5 围压450 kPa时G/Gmax-γ程序计算曲线与试验曲线对比
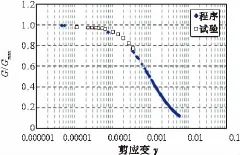
图6 围压700 kPa时G/Gmax-γ程序计算曲线与试验曲线对比
3.2 参数分析
由式8和式9可知,A,B,γ0三个拟合参数的取值对于Davidenkov模型的骨架曲线及滞回曲线均会产生一定的影响,本节研究A,B,γ0三个拟合参数取值的变化对于计算结果的影响。A,B,γ0的原始取值采用试样在围压为400 kPa时的参数,假设土体存在残余强度且破坏时剪切模量最小值取为0.05Gmax。
图7给出了当B和γ0保持不变时,A分别取0.9,1.1和1.3时的G/Gmax-γ曲线,从图中可以看出随着取值的增大,G/Gmax-γ曲线整体向上平移,曲线形状基本没有变化。图8给出了当A和γ0保持不变时,B分别取0.4,0.5和0.6时G/Gmax-γ的曲线,从图中可以看出同A值改变的情况不同,随着B值的增大,曲线没有出现平移,而是曲线下降段的斜率绝对值逐步增大。图9给出了当A和B保持不变时,γ0分别取0.0001,0.0003和0.0005时的G/Gmax-γ曲线,从图中可以看出,同A取值改变的情况相似,随着γ0取值的增大G/Gmax-γ曲线整体向上平移,曲线形状基本没有变化,且γ0取值越大,在γ0的变化量相同时,其曲线平移程度逐渐减小。

图7 围压400 kPa时拟合参数A对G/Gmax-γ曲线的影响
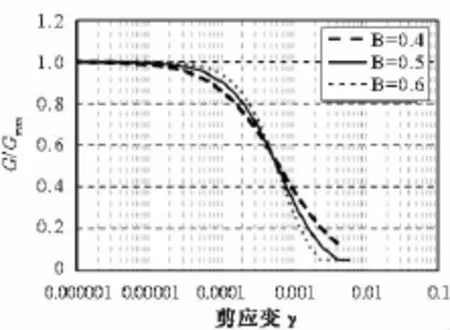
图8 围压400 kPa时拟合参数B对G/Gmax-γ曲线的影响
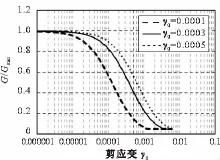
图9 围压400 kPa时拟合参数γ0对G/Gmax-γ曲线的影响
4 小结
本文以武汉典型软土作为研究对象,开展了共振柱试验,拟合了Davidenkov模型中的参数,通过有限元开源软件OpenSees的二次开发,编制Davidenkov模型的材料子程序并将其计算结果与试验结果进行对比以验证其正确性,最后通过所编制程序对Davidenkov模型中的参数进行敏感性分析,结果表明三个拟合参数中γ0的改变对于G/Gmax-γ曲线的影响程度是最大的。
[1]谢定义.土动力学[M].西安:西安交通大学出版社,1988.
[2]Hardin BO,Drnevich V P.Shearmodulusand damping in soils[J].Journal of the Soil Mechanics and Foundations Division,1972,98(7):667-692.
[3]Masing G.Eigenspannungen und Verfestigung Beim Messing[C]//Proceedings of the Second International Congress of Applied Mechanics.Zurich:1926:332-335.
[4]Martin P P,Seed H B.One-dimensional dynamic ground response analyses[J].Journal of the Geotechnical Engineering Division,1982,108(7):935-952.
[5]陈国兴,庄海洋.基于Davidenkov骨架曲线的土体动力本构关系及其参数研究[J].岩土工程学报,2005,27(8):860-864.
[6]庄海洋,陈国兴,梁艳仙,等.土体动非线性黏弹性模型及其ABAQUS软件的实现[J].岩土力学,2007,28(3):436-442.
[7]Gu Q,Conte JP.Convergence Studies in Nonlinear Finite Element Rsensitivity Analysis[C]//Proceedings of the Ninth International Conference on Applications of Statistics and Probability in Civil Engineering.San Francisco:Springer,2003:973-980.
Im plementation and App lication of Nonlinear Dynam ic Davidenkov Model of Soil in OpenSees
ZHAO Xu-qing
(China Railway 16th Bureau Group Company Limited,Beijing 100018,China)
Anti-seismic of underground structures is being focused gradually during the process of large-scale development.Due to its specialties,the research of the dynamic behavior of soil around underground structures is particularly significant.Soil dynamic mechanics characteristic includes nonlinear characteristic,hysteresis characteristic and the effectofstrain accumulated.Skeleton curves are fitted by measured data.In this paper,model parameters are fitted by resonant column tests,in which soft soil in Wuhan area was regarded as the research object.The Davidenkov model has been implemented into the OpenSees software as user-defined materials.The seismic response analysis of soilwas performed.
Davidenkovmodel;resonant column test;OpenSees;seismic response analysis
TU435
A
2095-0985(2015)02-0019-04
2015-01-21
2015-03-26
赵旭清(1970-),男,山西晋城人,高级工程师,博士,研究方向为交通土建应用技术(Email:zhaowuqingweb@sohu.com)

