高填方涵洞涵顶土压力影响因素敏感性分析

马强，朱健，肖衡林

(湖北工业大学土木工程与建筑学院，湖北武汉 430068)

高填方涵洞涵顶土压力影响因素敏感性分析

马强，朱健，肖衡林

(湖北工业大学土木工程与建筑学院，湖北武汉 430068)

高填方涵洞土压力受多种因素的影响。在对高填方涵洞受力影响因素归纳的基础上，筛选出埋设涵洞的沟谷宽度、沟谷边坡角度、地基土模量、填土模量、填土黏聚力和内摩擦角这6个主要影响因素，通过数值模拟对涵顶土压力系数的变化规律进行了分析，确定了上述6个因素产生有效影响的取值区间。根据正交试验原理，建立25个正交化数值模拟试验模型，针对上述6个主要影响因素，对高填方涵洞进行了影响因素敏感性分析，最后的极差分析结果表明，埋设涵洞的沟谷宽度和沟谷边坡角度是影响高填方涵洞涵顶土压力的最为主要和敏感的因素;填土模量、填土内摩擦角和地基模量对涵顶土压力有较显著影响;填土的黏聚力对涵顶土压力影响较小。

高填方涵洞;土压力系数;影响因素;敏感性分析;正交试验

山区公路建设往往会穿越沟谷地区，这些区域通常地形较为复杂，地层的分布也不均匀［1］，在山区建成的高填方涵洞大多存在不同程度的病害［2］。作为一种深埋构造物，高填方涵洞的受力受其几何尺寸、埋设方式、所处的地形和地质条件，路堤填料性质等诸多因素的影响［3，4］。在正确认识各种因素影响规律的基础上，开展涵洞受力影响因素敏感性分析，对高填方涵洞的设计和施工具有重要的意义。

目前为止，有关涵洞的研究多集中在涵顶土压力计算及对涵洞减载方面［5～7］，对涵洞受力影响因素的研究虽然也有不少的研究成果，这些工作主要是通过模型试验［8，9］或有限元计算［10，11］对比分析不同涵管孔径［12，13］、不同涵洞基础型式［14，15］，及不同填土高度时涵洞的受力状况。此外，部分研究工作分析了涵洞地基刚度和涵洞结构型式与尺寸等对涵洞受力的影响规律［16］。然而，这些研究工作对影响因素的分析仅考虑了单一变量所引起的土压力变化情况，没有分析各影响因素间的交互作用和土压力对各影响因素的敏感性。

在对影响涵洞受力的主要因素归纳分析的基础上，本文采用有限元计算手段，选择6个影响因素进行正交试验，分析这些影响因素交互作用下对涵洞受力的影响，并进行极差分析，对土压力系数受各因素影响的敏感性进行排序。

1 正交试验原理及流程

1.1 正交试验设计原理

单因素或两因素的试验，所分析的影响因素较少，采取全面试验时的分析规模也不算大。但试验因素较多时，如果采取全面试验分析，所需试验的数量、次数较多，受限于试验条件或时间原因，实施的可能性不大。这时就要从各因素的所有水平组合中挑选有代表性的部分组合进行试验。利用正交试验原理就可以解决这类问题。

正交试验设计就是从全面试验点中挑选出有代表性的部分点进行试验。正交设计在选择试验点时可利用正交表，正交表具有均匀分散、正交可比两大特点体现其正交性［17］。

1.2 正交模拟设计分析流程

根据正交试验原理，文中进行正交试验结合有限元分析的设计流程分四步:

(1)列出确定影响因素水平表;

(2)选择合适的正交表;

(3)正交试验方案设计及试验结果;

(4)对试验结果进行极差分析。

2 数值模型试验设计

2.1 计算参数与几何模型

将涵洞路段按照平面应变问题进行分析，采用PLAXIS有限元软件建立二维数值模型，在涵洞、填土和边坡等不同材料之间的接触面上使用接触单元来考虑摩擦作用。采用基于广义胡克定律的理想线弹性模型来描述涵洞洞身构件和基础，采用Mohr-Coulomb理想弹塑性模型描述地基土、边坡和填土，主要参数见表1。

表1 数值模拟参数

模型的几何条件如图1所示，采用板单元描述涵体构件的受力与变形特性，涵洞结构高h=8 m，基础宽度D=10 m，涵体宽度b=8 m。左右两侧山体边坡的坡角相等，均为β，涵洞左右侧墙到对应边坡的距离均为L。模型底部采用固定端约束水平向与竖向位移，模型两侧采用水平位移约束。

图1 涵洞路段几何模型示意

不同填土高度时的土压力系数数值模拟结果如图2所示。

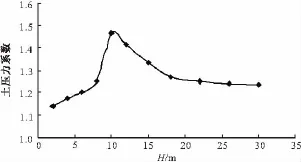
图2 土压力系数随涵顶填土高度变化规律

由图2可以看出涵顶填土高度在18 m以上，土压力系数趋于稳定，故在后述分析中选取涵顶填土高度H=18 m。

2.2 影响因素取值区间确定

在对文献归纳的基础上，选择影响涵洞受力的6个主要因素，包括沟谷宽度、涵洞所处沟谷边坡的角度、地基土模量、路堤填料的模量、黏聚力和内摩擦角进行分析，确定正交试验中各影响因素的取值区间。上述6个因素对涵顶土压力系数的影响规律如图3～8所示。

(1)沟谷宽度

有限元计算时几何参数取值为h=8.0 m，D =10 m，b=8.0 m，H=18 m，β=60°，使L发生变化，涵顶土压力系数变化规律如图3所示。

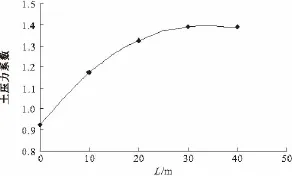
图3 侧墙到坡脚的距离对涵顶土压力系数的影响

由图3可知，沟谷地形对涵洞的有效影响宽度约为30 m。当L小于30 m时，涵顶土压力系数随L的增加而增大，当L大于30 m以后，涵顶土压力系数逐渐趋于稳定。

因此，在正交试验设计时选取沟谷宽度取值区间为0～30 m。

(2)边坡角度

有限元计算几何模型中取h=8.0 m，D=10 m，b=8.0 m，H=18 m，L=10 m，沟谷边坡的坡角β分别取10°、30°、50°、70°和90°进行数值模拟，所得涵顶土压力系数的变化规律如图4所示。

图4 边坡角度对涵顶土压力系数的影响

图4表明了边坡角度从10°向90°变化时，其对涵顶土压力系数均具有影响，故正交试验选取边坡角度取值范围10°～90°进行分析。

(3)地基土模量

有限元计算几何模型中取h=8.0 m，D=10 m，b=8.0 m，H=18 m，山体边坡坡角β=60°，H =10m，改变地基土的模量，得到涵顶土压力系数如图5所示。

由图5可以看出，地基土模量由1 MPa增大到20 MPa时，涵顶土压力系数变化较大，当地基土模量增大至40 MPa以后，涵顶土压力集中系数虽然继续增大，但增速减缓。同时，考虑地基模量常见的可能变化范围，正交试验选取地基土模量变化区间为1～60 MPa。

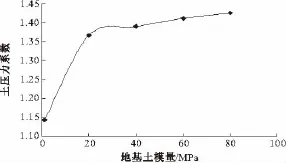
图5 地基模量对涵顶土压力系数的影响

(4)填土模量

为确定路堤填土模量、黏聚力、内摩擦角等填料性质对涵洞受力状态的影响规律，有限元计算模型中H=18 m，山体边坡坡角β=60°，L=10 m。分别改变路堤填土模量、黏聚力、内摩擦角等参数的取值进行数值模拟，所得涵洞土压力系数的变化规律如图6～8所示。

不同路堤填土模量时，涵顶土压力系数的变化规律如图6所示。当路堤填土模量从1 MPa增大到30 MPa时，涵顶土压力系数变化较大。当填土模量大于60 MPa后，涵顶土压力系数趋于稳定。同时，考虑填土模量可能变化的范围，正交试验选取填土模量变化区间为1～80 MPa。

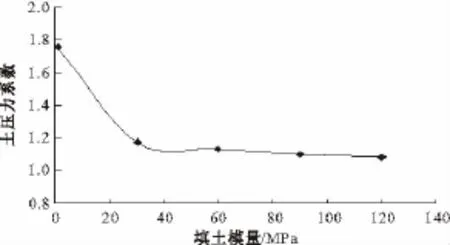
图6 填土模量对涵顶土压力系数的影响

(5)填土黏聚力

当路堤填土黏聚力发生变化时，涵顶土压力系数的变化规律如图7所示。由图7可以看出，填土黏聚力从0°增至40°时，涵顶土压力系数都会发生变化。正交试验选取黏聚力变化区间为0～40 kPa。

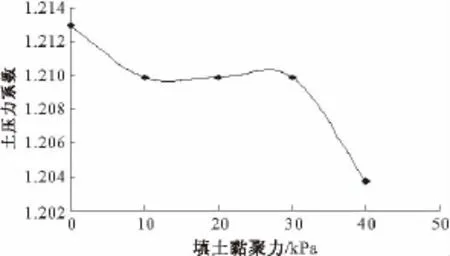
图7 填土黏聚力对涵顶土压力系数的影响

(6)填土内摩擦角

路堤填土内摩擦角变化时，涵顶土压力系数的变化规律如图8所示。随路堤填土内摩擦角的增加，涵顶土压力系数逐渐减小，填土内摩擦角由1°增大到60°时，涵顶土压力系数减小约0.09，正交试验选取填土内摩擦角变化区间为1°～60°。

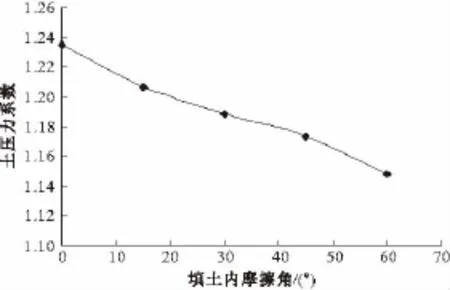
图8 涵顶土压力与路堤填土内摩擦角关系曲线

3 正交试验结果与极差分析

以上述分析为基础，确定了影响涵顶土压力6个因素变化区间，根据正交试验原理，按照5水平确定步长，各因素在不同水平的取值列于表2。

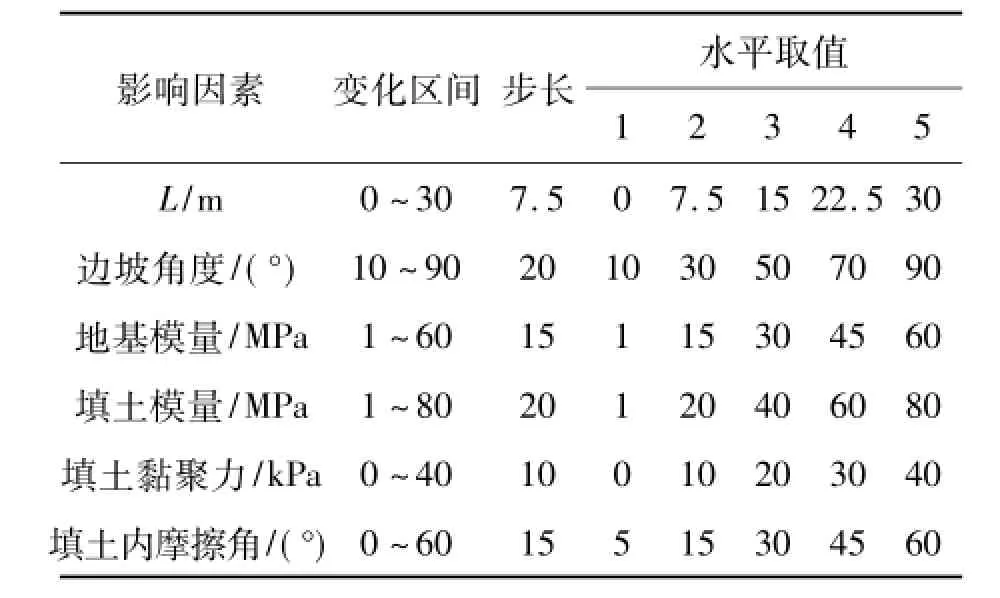
表2 涵顶土压力系数影响因素的水平取值

根据表2中各因素在不同水平的取值，进行6因素5水平正交试验，正交表如表3，其中因素1～6分别表示沟谷宽度、沟谷边坡角度、地基模量、填土模量、填土黏聚力和填土内摩擦角。各影响因素分别按照表3中的水平，在表2中选取对应水平的取值。对表3中25种组合情况分别建立有限元模型，计算涵顶土压力系数，计算结果列于表3。

由影响因素所对应的沟谷宽度、沟谷边坡角度、地基模量、填土模量、填土黏聚力和填土内摩擦角，进行正交组合后进行有限元计算，各因素在不同水平时涵顶土压力系数均值Kr及各因素在不同水平时涵顶土压力系数均值的极差R，如表4所示。

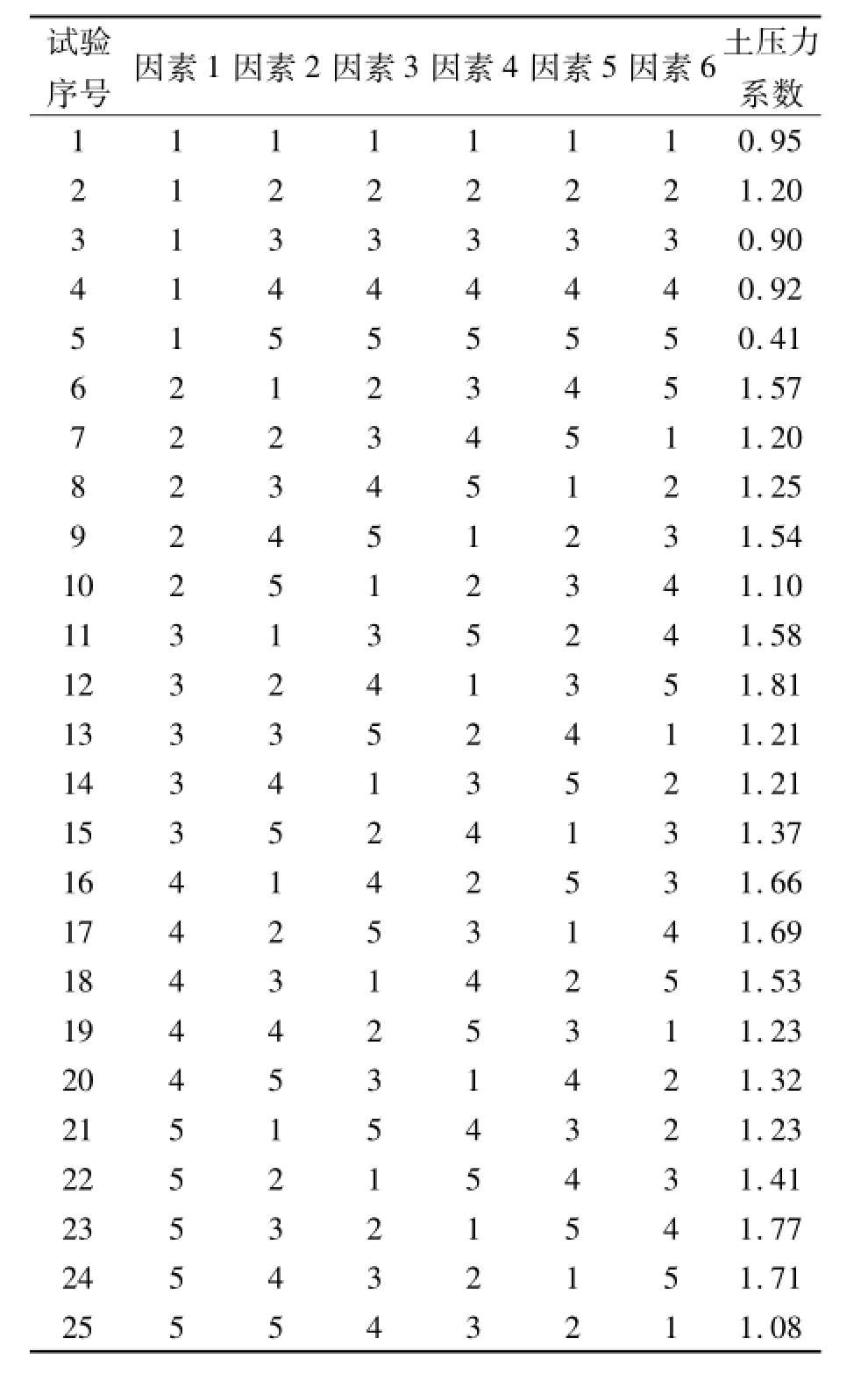
表3 L25(56)涵顶土压力影响因素的水平取值

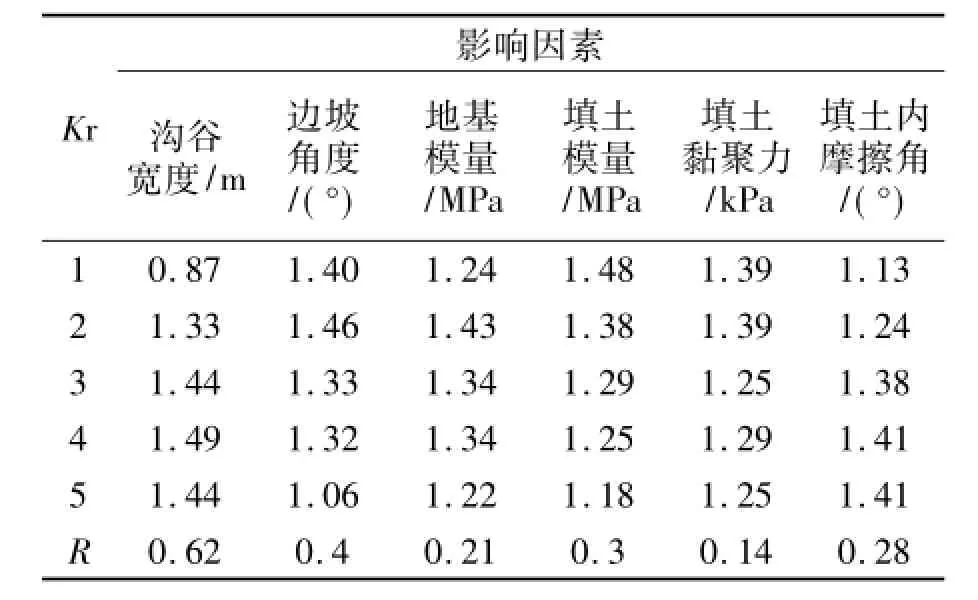
表4 涵顶土压力影响因素在各水平的Kr值及极差R

根据极差分析原理，极差越大说明因素对涵顶土压力系数的影响越大，由表4可以看出，沟谷宽度对应的极差为0.62，沟谷边坡角度极差为0.4，填土模量极差0.3，填土内摩擦角极差0.28，地基土模量极差为0.21，填土黏聚力极差0.14。按照极差的大小判断因素的主次顺序，影响因素的主次顺序为:

沟谷宽度＞沟谷边坡角度＞填土模量＞填土内摩擦角＞地基模量＞填土黏聚力

即沟谷宽度及沟谷边坡角度对涵顶土压力的影响最大，故在涵洞埋设时必须注意所埋设沟谷地形的影响，特别是在涵洞左右两侧地形或到沟谷距离有明显差异时，尤其要注意地形条件所引起的涵洞结构受力的非对称性。其次是路堤填土模量和填料内摩擦角对涵顶土压力的影响，可以采用具有较高模量的填筑材料，或具有较大内摩擦角的材料作为路堤填料，以利于减小涵顶的土压力值。地基模量对涵顶土压力具有一定的影响，该因素的影响规律与其他因素相反，地基模量大时，涵顶土压力也会增大。由于地基土的压缩性也反映地基承载力的高低，工程中不宜人为减小地基模量，以避免承载力不足或过大的沉降。

4 结论

本文通过根据正交试验原理，利用数值模拟对涵洞受力的6个主要影响因素进行的敏感性分析，得到如下主要结论:

(1)沟谷宽度对涵顶土压力有效影响宽度为30 m;沟谷边坡角度变化时，土压力系数发生波动，坡角在30°和70°左右时，土压力系数较小;地基土模量在0～20 MPa时，对涵顶土压力系数影响明显;填料模量由1 MPa增大到30 MPa，涵顶土压力系数变化显著。

(2)各因素对涵顶土压力影响大小依次为沟谷宽度、沟谷边坡角度、填土模量、填土内摩擦角、地基模量、填土黏聚力。

根据上述结论不仅可判断出各影响因素的主次，而且在判明影响因素对土压力系数影响趋势的基础上，预计出各影响因素取值将产生的土压力系数系统响应。可为涵洞的设计和施工以及涵洞减载方法确定提供指导和参考。

［1］郑俊杰，马强，陈保国.高填方涵洞地基承载力分析［J］.华中科技大学学报(自然科学版)，2009，37(4):115-118.

［2］顾安全.上埋式管道及洞室垂直土压力的研究［J］.岩土工程学报，1981，3(1):3-15.

［3］马强，郑俊杰，张军.山区涵洞受力影响因素的数值模拟分析［J］.合肥工业大学(自然科学版)，2009，32(10):1514-1517.

［4］Chen Baoguo，Zheng Junjie，Han Jie.Experimental study and numerical simulation on concrete box culverts in trenches［J］.Journal of Performance of Constructed Facilities，2010，24(3):223-234.

［5］郑俊杰，马强，张军.加筋减载涵洞的涵顶土压力计算［J］.岩土工程学报，2011，33(7):1135-1141.

［6］Zheng Junjie，Luo Depi，Ma Qiang.Numerical analysis of slab culvert beneath imperfect ditch covered with geogrid layers［J］.Applied Mechanics and Materials，2011，71-78:3338-3341.

［7］马强，郑俊杰，张军.高填方涵洞加筋减载的现场试验研究［J］.岩土力学，2012，33(8):2337-2342.

［8］李永刚，李力.钢筋混凝土涵洞顶部垂直土压力影响因素研究［J］.长江科学院院报，2006，23 (6):72-74.

［9］杨锡武，张永兴.公路高填方涵洞土压力变化规律及计算方法研究［J］.土木工程学报，2005，38 (9):119-124.

［10］寇宏刚，马强，母进伟，等.装配式盖板涵构件搭接强度分析［J］.土木工程与管理学报，2012，29(4):41-44.

［11］马强，郑俊杰，张军，等.高填方涵洞减载机制与数值分析［J］.岩土力学，2010，31(s1):424-429.

［12］许建军，张峻峰.关岭至兴仁公路涵洞布置与选型［J］.中国港湾建设，2002，(1):47-48.

［13］张发祥.拱形涵洞的受力分析和选型［J］.河海大学学报，1995，23(3):58-63.

［14］陈素君.高填土涵洞的基础设计［J］.公路，1998，(4):37-39.

［15］刘保健，谢永利，程海涛，等.上埋式公路涵洞地基及基础的设计［J］.长安大学学报(自然科学版)，2006，26(3):17-20.

［16］陈保国，骆瑞萍，孙金山.上埋式盖板涵受力特性及影响因素研究［J］.岩土力学，2011，32(1): 199-206.

［17］高允彦.正交及回归试验设计方法［M］.北京:冶金工业出版社，1988.

Orthogonal Polar Difference Analysis for Sensitivity of the Factors Influencing the Earth Pressures on High Embankment Culvert

MAQiang，ZHU Jian，XIAO Heng-lin
(School of Civil Engineering and Architecture，Hubei University of Technology，Wuhan 430068，China)

The earth pressure of high embankment culvert is influenced bymany internal and external factors.Based on the induction of factors influence the earth pressure on high embankment culvert，the valleywidth，slope angle，substrate soilmodulus，modulus，cohesion and internal friction angle of embankment fill are screened out as the 6 main influencing factors.The variations of coefficient of earth pressure on the crown of culvert are analyzed via numerical simulation，and the range of the factors have effective influence on the earth pressure are determined.According to the principle of orthogonal test，25 numericalmodels are installed for the analysis of the sensitivity of influence factors on the earth pressures on high embankment culvert.The results show that，thewidth and slope angle of the trench are themost important and sensitive factors for the earth pressures on the crown of the high embankment culvert.The modulus and friction angle of the backfill，as well as the subgrade modulus have secondary significant effect on the earth pressure.However the cohesion of the backfill has little effect on the earth pressure.

high embankment culvert;the coefficient of earth pressure;influencing factor; sensitivity analysis;orthogonal test

U449

A

2095-0985(2015)02-0008-05

2015-01-06

2015-03-02

马强(1983-)，男，湖北丹江口人，副教授，博士，研究方向为岩土工程(Email:maqiang927@163.com)

国家自然科学基金(51208187);黄土地区公路建设与养护技术交通行业重点实验室开放课题(KLTLR－Y12－11)