浅析“向量坐标系”在解题中的应用

☉江苏省苏州市田家炳实验高级中学 王 耀

浅析“向量坐标系”在解题中的应用

☉江苏省苏州市田家炳实验高级中学 王 耀

文1中，笔者通过建立“向量坐标系”解决了一类高考题.事实上，对“”这种形式的许多问题，［2］还可利用平面向量基本定理去进一步研究“向量坐标系”，并通过与平面直角坐标系的类比，得到向量坐标系中的一些重要推论，从而可直接基于向量视角顺利解决问题.

一、“向量坐标系”的三要素

1.认识“向量坐标系”中的“点”的属性

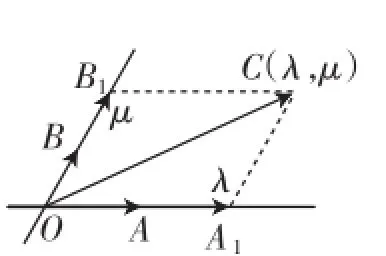
图1

2.分析“向量坐标系”中的距离、夹角和数量积

这里，以刚结束的一道2014年卓越联考自主招生试题为例来研究“向量坐标系”中的两点距离问题.

试题 n1、n2是两个夹角为θ的单位向量，以n1、n2为基的坐标系中，A（x1，y1），B（x2，y2），求|AB|.

首先，以n1方向为x轴建立平面直角坐标系，此时n1=（1，0），n2=（cosθ，sinθ），那么由A（x1，y1）知得到A（x1+y1cosθ，y1sinθ）；同理，可知B（x2+y2cosθ，y2sinθ），则可得到|AB|=

事实上，若建立向量坐标系的话，只要通过向量基本运算即可得到同样的结果，这也说明选择不同的坐标系，距离是不变的.具体解法如下：

设n1、n2的交点为O，则那么=（x2-x1）n1+（y2-y1）n2，那么（y2-y1）2+2（x2-x1）（y2-y1）n1n2，利用n1n2=cosθ即可解得

此时，即可探究向量坐标系中的两个向量的数量积定义与计算公式，不妨设a=一方面：a·b=（x1n1+y1n2）·（x2n1+y2n2）=x1x2+y1y2+（x1y2+ x2y1）n1·n2=x1x2+y1y2+（x1y2+x2y1）cosθ； 又由定义a·b=，及余弦定理：=|a|·|b|·cos〈a，b〉，则可知在向量坐标系中，向量数量积a·b=|a|·|b|·cos〈a，b〉仍然成立，这与平面直角坐标系中的结论一致.并且，向量极化恒等式a·b=和平行四边形公式|a+b|2+|a-b|2=2（|a|2+|b|2）依然成立.

3.探究“向量坐标系”中的“线”的本质

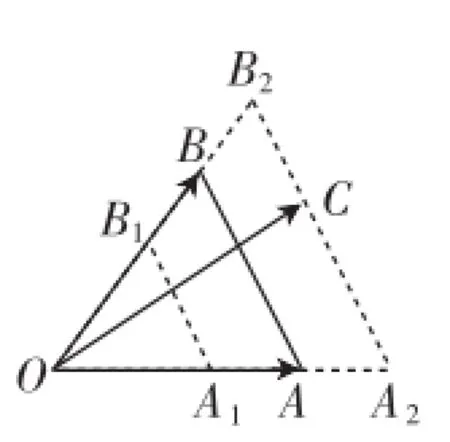
图2

文1中，基于平面向量基本定理的推论进一步讨论了一类可化为“”的向量值线性规划区域问题，即将问题转化为共起点的基底向量，从而研究k= λ+μ的取值范围，其中k=，如图2所示.那么，对于向量坐标系中任意的一条线aλ+bμ=c（a，b，c∈R）又表示何种意义呢？首先，分别考虑如下情形.

评注：事实上，此处也可用平面几何知识，过点C分别作OA、OB的平行线，由平行线分线段成比例定理更容易得到，同理也能够得到向量在直线μ=λ上.

二、例题赏析

例1 （1）（2013年北京（文）14）已知点A（1，-1），B（3，0），C（2，1）.若平面区域D由所有满足（1≤λ≤2，0≤μ≤1）的点P组成，则区域D的面积为_________.

（2）（2014年福建预赛8）已知点A（1，-1），B（4，0），C（2，2）.平面区域D由所有满足（1＜λ≤a， 1＜μ≤b）的点P（x，y）组成.若区域D的面积为8，则a+b的最小值为_________.

（3）已知-1≤x≤3，1≤y≤4，|a|=1，|b|=2，〈a，b〉=60°，则|xa+yb|的取值范围为_________.

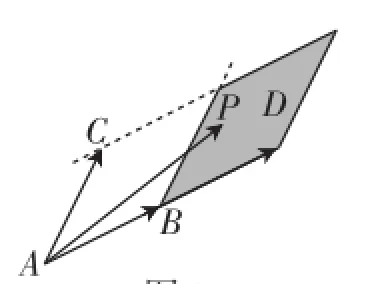
图3

那么区域D的形状为平行四边形，夹在两对平行线λ=1，λ=2与μ=0，μ=1之间，其面积与以为邻边的平行四边形面积相等，即

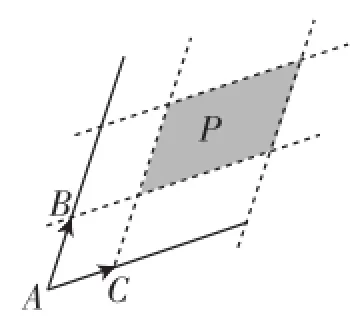
图4

由题意可知SP=（a-1）8（a-1）（b-1）=8，即（a-1）（b-1）=1.

（3）建立向量坐标系（如图5），分别作直线x=-1，x=3，y=1，y=4，易知|xa+yb|min=|m|，|xa+yb|max=|n|.

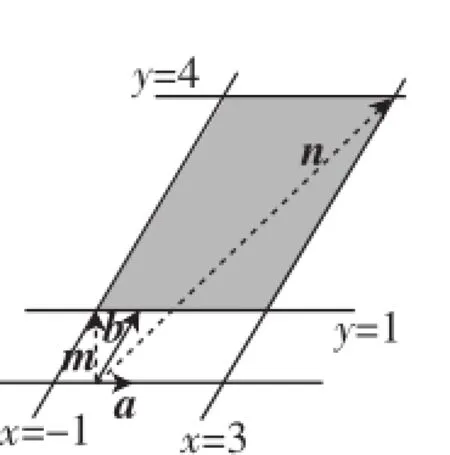
图5

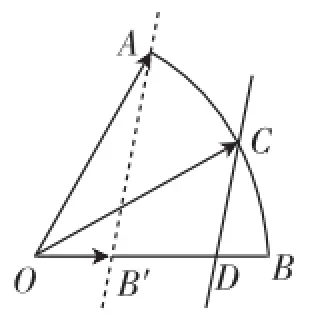
图6

例2（1）（2013年浙江省杭州市高三一模17）如图6，在扇形OAB中，∠AOB=60°，C为弧AB上的一个动点，若则x+3y的取值范围是_________.

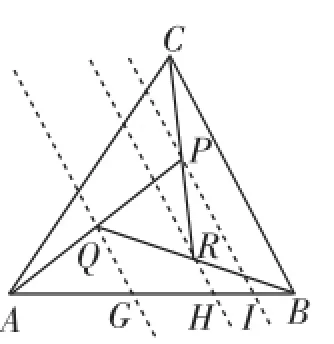
图7

（3）（2014年浙江省宁波市高三模拟）已知点O是△ABC的外心（外接圆的圆心），且AB= 3，AC=4，若存在非零实数x，y，使得且x+ 2y=1，则cos∠BAC=_________.

图8

（4）（2014年苏锡常镇高三第一次调研12）如图8，在△ABC中，BO为边AC上的中线，，则λ的值为_________.

（2）如图7所示，分别过点Q、R、P作BC的平行线，分别交AB于G、H、I三点，则可设AG=GI=x，IB=y，HI=z；BH= GH=y+z，那么AB=AG+GH+IB=x+x+y；AB=BH+HG+AG= 2（y+z）+x.由此可知x=y+2z.又由P为CR的中点，可知HI= IB，即y=z，那么x=3z.因此，由可知m+n==

评注：此题中若没有“若存在非零实数x、y”这个条件，结果将会发生变化.通过上述解析过程发现，当x=0， y=时，△ABC的外心点O和点D重合，此时△ABC为直角三角形，且AB⊥BC，则cos∠BAC=，故结果将会有两解.

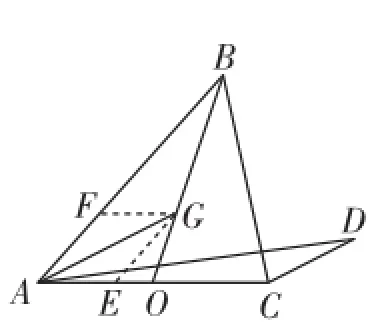
图9

（4）在图9中，过点G作AB的平行线交AO于点E，作AC的平行线交AO于点F，由可知即有=；同理那么

例3 （1）（2014届成都二诊数学（文科）试题15）已知单位向量i、j的夹角为θ（0＜ θ＜π，且θ≠），若平面向量a满足a=xi+yj（x，y∈R），则有序实数对（x，y）称为向量a在“仿射”坐标系Oxy（O为坐标原点）下的“仿射”坐标，记作a=（x，y）θ.有下列命题：

①已知a=（2，-1）θ，b=（1，2）θ，则a·b=0；

③已知a=（x1，y1）θ，b=（x2，y2）θ，则a-b=（x1-x2，y1-y2）θ；

④已知=（1，0）θ，=（0，1）θ，则线段AB的长度为2sin

其中为真命题的是________（写出所有真命题的序号）.

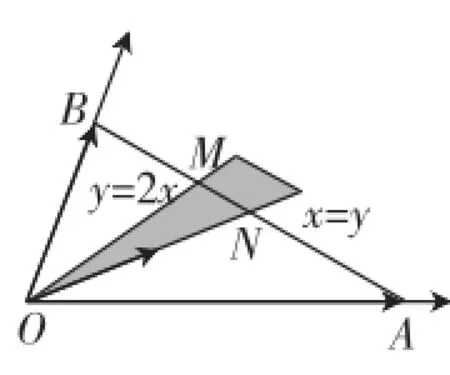
图10

①x≥0，y≥0；②x-y≥0；③x-y≤0；④x-2y≥0；⑤2x-y≥0.

解析：（1）①由前文分析知a·b=（2i-j）·（i+2j）=3i·j= 3cosθ，当且仅当θ=90°时，a·b=0.故①错.

②在向量坐标系下考虑，若向量a、b的夹角取到最小值0时，则向量a、b共线且同向，那么x=y＞0；反之，若x= y＜0时，向量a、b共线但是反向，故它们夹角取到最大值π.因此，②错.

③a-b=（x1-x2）i+（y1-y2）j=（x1-x2，y1-y2）θ.

综上可知，③④为真命题.

（2）建立如图10所示的“向量坐标系”，仿照平面直角坐标系，首先同样得到：x≥0，y≥0.

此外，线段MN上满足x+y=1；右上方的平行线段上满足x+y=k（k＞1）.故图10中所示区域内的系数满足：

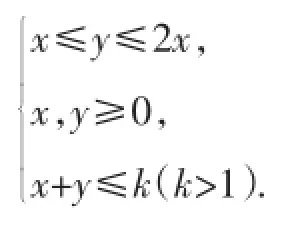
三、题后总结

文中，笔者从纯向量的角度分析了“向量坐标系”的特性，并成功应用到一系列可化为此背景的高考或模考试题中.常规做法主要是建立直角坐标系进行向量坐标运算或者直接利用向量基本运算，这种传统的处理方式在解决问题时，耗时耗力；而本文提供的这种“几何通法”的优势主要体现在：利用平面向量的基本定理，将一类涉及基底的线性表示系数之和的问题，化归为建立基底“向量坐标系”进行问题分析.这种做法既能避免烦琐的代数运算，又能够充分体现向量的“形”的几何优势，将“形”的魅力展现到极致.

在教学中，要对重要知识点有选择地“把书读厚”，即指要让学生明白知识的核心和本质是什么，它的上位知识是什么，以及构成知识的基本要素又有哪些，它的用处在哪儿.结合对文中相关内容的教学实践来看，笔者并没有涉及“仿射坐标系”等高深的概念，而是直接用“向量坐标系”来描述，并且通过与平面直角坐标系的类比而研究得到向量坐标系中的许多性质，这样的处理方式适合学生的认知结构，避免让学生觉得很难很高深，反而容易被学生理解和掌握.［3］

综上所述，作为教师，要了解知识体系结构，深谙个中的关系，并自觉地指导和帮助学生认识问题，参悟本质，形成思维.只有这样，作为求知者的学生，才能从被动的解题中解放出来，知晓知识的来龙去脉，深究核心知识的数学本质，从而做到了然于心，方能运用自如.

1.王耀.一类可化为向量值线性规划问题的研究及其应用［J］.中学数学（上），2014（3）.

2.蒋明建.破解向量难题 挖掘潜在信息［J］.中学数学（上），2013（9）.

3.齐民友.中学数学教学中的向量［J］.数学通报，2007（4）.F