问题表述多元性 等价转化变直观——解答函数问题中的转化思想

☉江苏省宿迁中学 徐红兵

问题表述多元性 等价转化变直观
——解答函数问题中的转化思想

☉江苏省宿迁中学 徐红兵

“化归与转化思想”是高中数学几大常规数学思想之一，数学解题的过程也可以称之为转化的过程，即将复杂问题简单化、抽象问题直观化、未知转化为已知、一般问题化为特殊问题等，本文以近几年高考中的函数问题为例，就解题中所涉及的转化思想分析说明，供同学们复习参考.

一、巧借对称——化被动为主动

对称性是函数的重要性质之一，主要包括函数图像关于x轴或y轴对称、关于某条直线对称、关于原点对称、关于某一点成中心对称，其中既包括函数自身的对称性，也包括两函数之间的对称性.

例1 （2014年高考湖南卷）已知函数f（x）=x2+ex-（x＜0）与g（x）=x2+ln（x+a）的图像上存在关于y轴对称的点，则a的取值范围是（ ）.

解析：已知函数f（x）=x2+ex-（x＜0）与g（x）=x2+ ln（x+a）的图像上存在关于y轴对称的点，则问题可等价转化为函数f（x）=x2+ex-（x＜0）关于y轴对称的函数f（-x）=（-x）2+e-x-与g（x）=x2+ ln（x+a）的图像有交点，即（-x）2+e-x-=x2+ln（x+a）有解，化简得e-x-=ln（x+a），结合图像（如图1）.

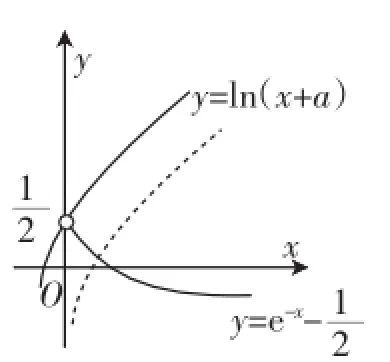
图1

评注：本题解答中，将两函数存在关于y轴对称的点，对称转化为两个函数的交点问题，进而将问题求解.在利用函数的对称性求解相关问题时，要注意变量的变与不变.

二、等价换元——化陌生为熟悉

化陌生为熟悉，是等价转化思想的精髓所在，高中数学解题的过程，其实就是化生为熟的过程，即将陌生的问题化为我们熟悉的问题解答.

例2 （2014年高考全国）若函数f（x）=cos2x+asinx在区间上是减函数，则a的取值范围是_________.

解析：f（x）=cos2x+asinx=-2sin2x+asinx+1，令sinx=t，则f（x）=-2t2+at+1.因为x∈），所以t∈所以f（x）=-2t2+at+1，t∈因为f（x）=cos2x+asinx在区间上是减函数，所以f（x）=-2t2+at+1在区间上是减函数.又对称轴为x=，所以，即a∈（-∞，2］.

评注：本题解答中，经过换元将陌生的函数化为我们熟悉的二次函数，进而利用二次函数最值问题求解.

三、参数分离——化烦琐为简洁

参数分离，即将参数从已知所给的函数关系中分离出来，使问题转化为确定的函数与常数函数（参数为常数）之间的关系，进而将问题简洁求解.

例3 （2014年高考天津）已知函数f（x）=|x2+3x|，x∈R.若方程f（x）-a|x-1|=0恰有4个互异的实数根，则实数a的取值范围为_________.

图2

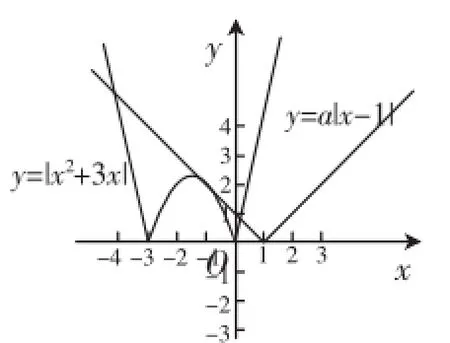
图3

评注：本题也可在同一坐标系内分别作出y=f（x）与y= a|x-1|的图像，如图3所示.当y= a|x-1|与y=f（x）的图像相切时，由整理得x2+（3-a）x+a=0，则Δ=（3-a）2-4a=a2-10a+9=0，解得a=1或a= 9.故当y=a|x-1|与y=f（x）的图像有4个交点时，0＜a＜1或a＞9.

四、分类讨论——化不定为确定

在众多函数问题中，大部分都带有参数，因参数的取值范围不同，造成函数的解析式、图像、性质不同，因此在解题中对参数的分类讨论必不可少.

例4 （2014年高考湖北）已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=（|x-a2|+|x-2a2|-3a2）.若∀x∈R，f（x-1）≤f（x），则实数a的取值范围为（ ）.

因此，根据奇函数的图像关于原点对称作出函数f（x）在R上的大致图像，如图4.

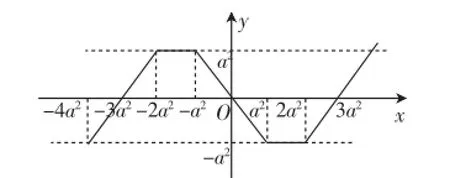
图4

观察图像可知，要使∀x∈R，f（x-1）≤f（x），则需满足2a2-（-4a2）≤1，解得-.故选B.

评注：分类讨论的运用，可将复杂的问题分解为几个基本的简单问题，进而各个击破.应用分类讨论的过程中，要注意分类标准的选择不重复、不遗漏.本题以x的取值为分类标准，将不确定的函数关系式转化为确定的函数关系式，使问题得以顺利解决.

五、借助具体函数——化一般为特殊

近几年来全国及各省市的高考题都或多或少地出现了一些我们从未见过的新题型，面对这些挑战时，有些学生不知所措，其实“新”并不等于“难”，题型“新”不等于解法“新”.

例5 （2013年高考福建）设S、T是R上的两个非空子集，如果存在一个从S到T的函数y=f（x）满足：

（1）T=｛f（x）|x∈S｝；

（2）对任意x1、x2∈S，当x1＜x2时，恒有f（x1）＜f（x2），那么称这两个集合“保序同构”.

以下集合对不是“保序同构”的是（ ）.

A.A=N*，B=N

B.A=｛x|-1≤x≤3｝，B=｛x|x=-8或0＜x≤10｝

C.A=｛x|0＜x＜1｝，B=R

D.A=Z，B=Q

解析：对于选项A，取f（x）=x-1，x∈N*，满足条件，所以A=N*，B=N是“保序同构”，应排除A.

故选D.

评注：从陌生的情景中寻找已学过的函数知识背景，设法建立沟通已知与未知的联系，寻求转化的途径是本题求解的关键.解答中所运用的排除法是解决选择题的一个重要方法，根据所给的条件，构造出符合条件的函数，进而利用特殊函数的性质得出结论.F