考虑输入受限和自动驾驶仪延迟的自适应滑模制导律

宋俊红，宋申民

考虑输入受限和自动驾驶仪延迟的自适应滑模制导律

宋俊红，宋申民

（哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001）

在输入受限的情况下，为了满足导弹拦截机动目标时高精度制导的需求，首先建立了满足输入受限和考虑导弹自动驾驶仪一阶动态特性的制导模型，其把目标加速度视为未知有界的外界干扰，通过设计自适应控制估计干扰的上界来避免对干扰上界的先验要求，同时结合滑模控制，设计了一种考虑输入受限和自动驾驶仪延迟的自适应滑模制导律，并且基于Lyapunov稳定性理论证明了制导系统状态渐进收敛到零。最后，在所设计的制导律下，对目标余弦机动和阶跃机动两种情况进行了仿真，得到的脱靶量分别为0.040 m和0.036 m，拦截时间分别为6.460 s和7.833 s。仿真结果表明所设计的制导律不仅保证导弹有效击中目标，并且具有较高的制导精度。

制导律；自动驾驶仪延迟；输入受限；自适应控制；滑模控制

在实际制导过程中，导弹自动驾驶仪的动态延迟严重影响着制导精度，尤其在目标存在机动的情况下，如果不考虑导弹自动驾驶仪动特性，制导精度就很难得到保证。因此，有必要对考虑自动驾驶仪动态特性的制导律进行深入研究，以获得较高的制导精度。文献[1-2]运用滑模控制理论设计制导律，并考虑了自动驾驶仪的一阶动态特性，在所设计的制导律下，制导系统状态有限时间收敛到零。文献[3-4]均考虑自动驾驶仪的一阶动态特性，运用反步法设计制导律，保证系统状态渐进收敛到零。另外，在考虑自动驾驶仪的制导律设计中，也有用二阶动态特性来描述自动驾驶仪的动特性，例如文献[5]应用动态面控制方法设计一种新型制导律。针对制导律和自动驾驶仪整体设计的研究，还有基于最优控制理论[6]、次最优控制[7]、Lyapunov稳定性理论[8]等设计的制导律。

然而，上述制导律在设计的过程中都没有对控制输入受限问题加以考虑，而这在实际的导弹制导过程中却是不容回避的。至今，已有许多学者对基于一些控制方法解决控制输入受限的问题进行了研究[9-12]。但是在导弹制导律设计中考虑控制输入受限问题的研究比较少。文献[13]通过运用滑模控制设计了一种带有输入受限的三维制导律。文献[14]也设计了一种三维的新型非线性模糊H∞制导律，该制导律在设计过程中也考虑了执行机构饱和问题。目前对同时考虑导弹自动驾驶仪动态特性和控制输入受限的制导问题研究相对较少。因此，设计一个考虑自动驾驶仪动态延迟且满足输入受限条件的制导律是十分必要的。

针对导弹拦截机动目标的带有控制输入受限的末制导问题，将目标加速度视作外界干扰，通过运用自适应律对其上界进行估计，并结合滑模控制方法提出了一种考虑自动驾驶仪动态特性的自适应滑模制导律。所提出的制导律不仅能够在满足输入受限约束下使得系统状态渐进收敛到零，同时不需要知道外界干扰上界的信息。通过仿真验证本文提出制导律的有效性。

1 问题描述

以平面拦截为例，导弹-目标相对运动关系如图1所示。为了简单起见，一般选取在攻击平面内的水平线作为基准线，由导弹指向目标的连线作为视线，由图1可以导出如下相对运动学方程[15]：

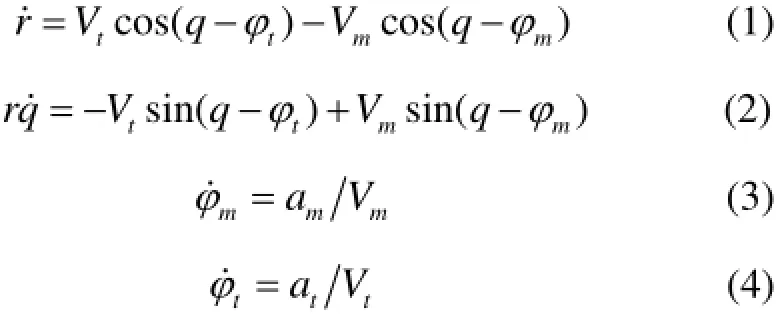
式中：r、r˙分别代表导弹和目标之间的相对距离和相对速度；mφ、tφ分别代表导弹和目标的速度方向角，若从基准线逆时针转到各自的速度矢量上，则mφ、tφ为正；q、q˙分别代表视线角和视线角速度，若从基准线逆时针转到视线上时，则q、q˙为正；ma、ta分别代表导弹和目标的法向加速度；mV、tV分别代表导弹和目标的速度，假设它们是常值。

对式(1)和式(2)相对于时间求一阶导数，得到

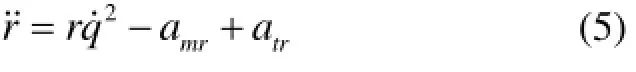
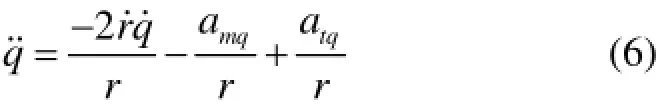
式中：amr=amsin(q-φm)、atr=atsin(q-φt)分别是导弹加速度和目标加速度在视线方向上的分量；amq=amcos(q-φm)、atq=atcos(q-φt)分别是导弹加速度和目标加速度在视线法向上的分量。

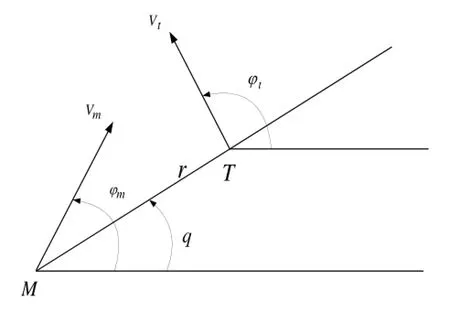
图1 导弹和目标相对运动关系Fig.1 Relative motion geometry of missile and target

导弹的自动驾驶仪动态特性用一阶惯性环节来描述，如下：

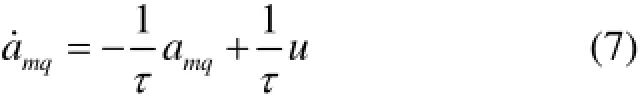
式中：τ为导弹自动驾驶仪时间常数，u为提供给导弹自动驾驶仪的制导指令。

本文的设计目的是提出一种制导律，保证导弹能够获得较小的脱靶量。也就是说，在目标存在机动的情况下，我们通过设计导弹自动驾驶仪的制导指令u使得视线角速率q˙渐进收敛到零。

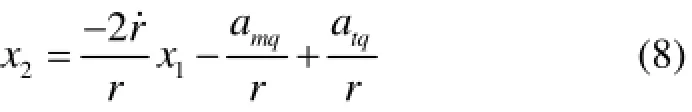
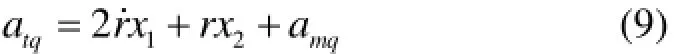
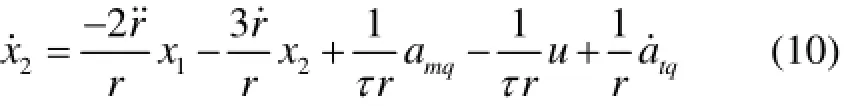
结合式(8)和式(10)可得考虑自动驾驶仪动特性的制导系统状态方程为

2 制导律设计

考虑导弹自动驾驶仪的制导指令u的输入受限约束条件，制导系统状态方程(11)改写成如下形式：

式中，饱和函数sat()u的定义为

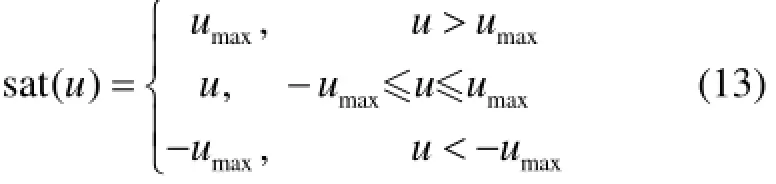
式(13)中，maxu是自动驾驶仪所能提供的制导指令的最大值，其是一个已知的正常数。

为了简便起见，饱和函数sat()u可以写成

式中，

根据文献[9]，实际的制导系统中存在一个未知常数δ满足0＜δ≤min(h(u ))≤1。

对于考虑输入受限和自动驾驶仪延迟的制导系统状态方程(12)，在外界干扰存在的情况下，设计制导律u使得状态变量1x和2x渐进收敛于零。同一般的滑模控制方法设计相似，首先是设计滑模面，来获得所期望的控制效果。则选取如下线性滑模面：

式中，0k＞为设计常数。

为了让制导系统状态快速地从初始状态收敛到滑模面(16)，选择以下的快速幂次趋近律：

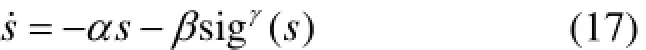
在描述定理之前，先给出如下的引理和假设。

引理 1[16]对于考虑输入受限和自动驾驶仪的制导系统(12)，如果滑模面s满足s=0，那么，进而可得到x1=0和x2=0。

假设1 d被视为总的外界干扰，在实际制导过程中是个有界量，并且满足其中c1,c2,c3是未知的正常数。

定理 1 针对考虑输入受限和自动驾驶仪延迟的制导系统(12)，在假设1成立和选取滑模面(16)的情况下，在以下设计的制导律(18)的作用下，滑模面渐进地收敛到零，进而视线角速度x1和视线角速度的导数x2渐进地收敛到零。

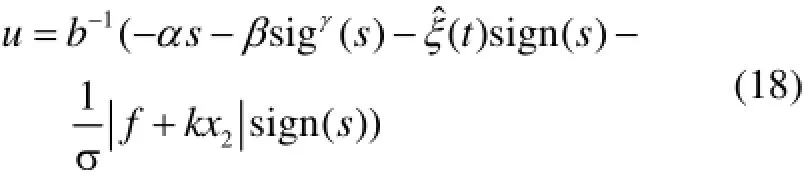
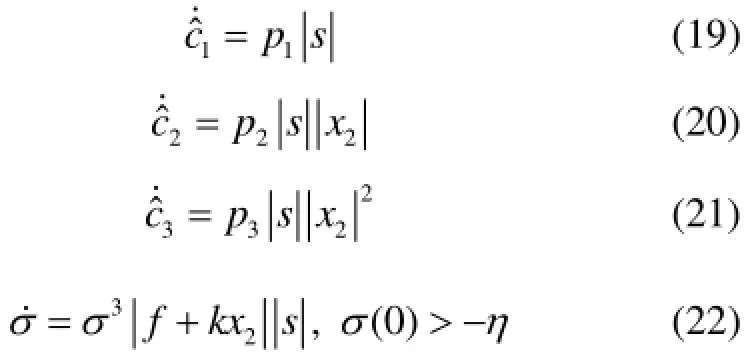
式中，p1,p2,p3＞0，η＜0。

证明：选取Lyapunov函数

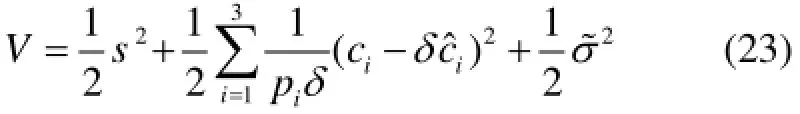
式中，σ˜=η-σ-1。 对V求导后可得

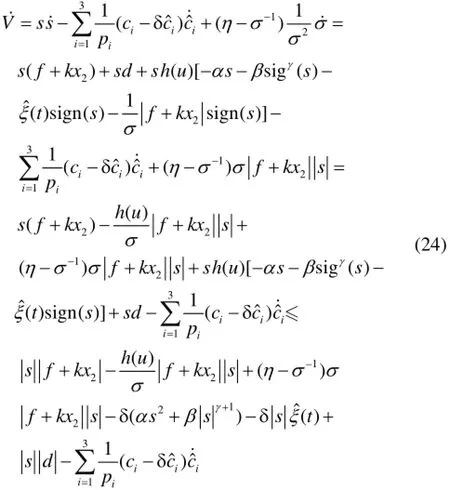
因为0()1hu＜≤，0η＜，()0tσ＞, 则有

由式(25)可得下面不等式成立：

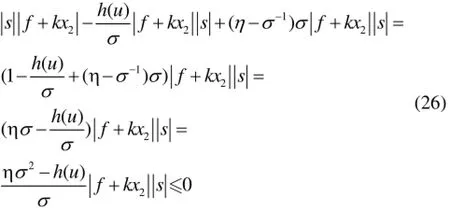
进一步由式(24)和式(26)可得

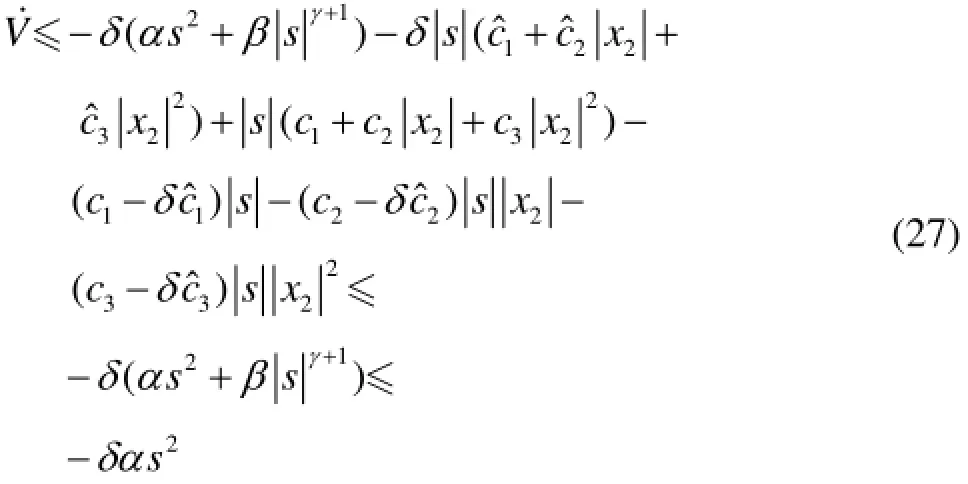
证毕。

注1 在本文所设计的制导律(18)式中，由于符号函数sign()s的存在导致制导律不连续，产生抖振现象。为了削弱抖振，选用连续的饱和函数sat()s代替符号函数sign()s，饱和函数表达式如下：

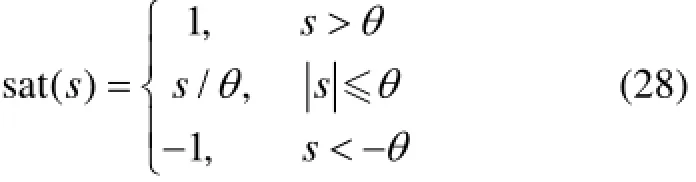
式中，θ是一个非常小的正数。

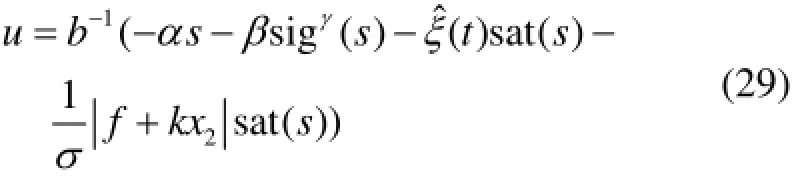
用饱和函数sat()s(28)替换符号函数sign()s代入式(18)，修改后的制导律为注2 从制导律式(29)中可以看出，制导律的实施需要知道x2=x˙1=˙q的信息，但是在实际制导中，q˙是不能够直接测量得到的。对此，本文应用滑模微分器[17]来获得q˙的估计值。令和分别是x1和x1的一阶导数的估计值。设计如下形式的滑模微分器：

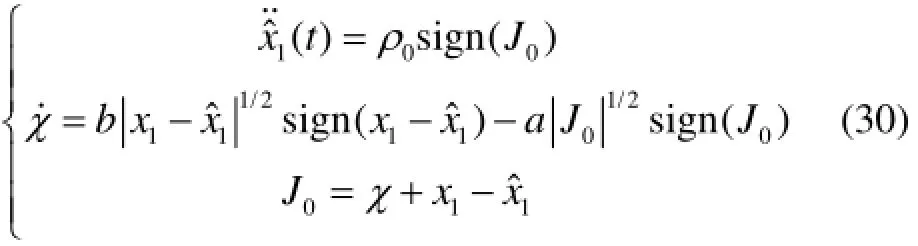
如果选择合适的常数0ab＞＞和00ρ＞，那么系统式(30)能够保证和在有限时间内分别收敛到1x和。

3 数字仿真

在本文的仿真实验中，制导系统的初始状态选择如下：导弹目标的初始相对距离为r(0)=5000 m，初始时刻的视线角为q(0)=30°，导弹的速度Vm=600 m/s，导弹的初始速度方向角φm(0)=20°，目标的速度Vt= -300 m/s， 目标的初始速度方向角φt(0)=-10°。重力加速度为g=9.8 m/s2，导弹自动驾驶仪所能够提供的最大制导指令为40g，导弹自动驾驶仪的动态参数为τ=0.5。

在设计的制导律式(29)中，参数选取为α=1，β=1，γ=0.9，k=10，p1=p2=p3=0.1，θ=0.002。为了更好地说明本文所提出的带有输入受限和考虑自动驾驶仪延迟的制导律(29)的性能，目标分为at=7gcos((π4)t )m/s2的余弦机动和的阶跃机动两种情况进行仿真。仿真结果分别如图2(a)-2(f)、图3(a)-3(f)和表1所示。

从图2(a)-2(b)和3(a)-3(b)所示的视线角速度和滑模面曲线可以清楚地看到，针对目标余弦机动和阶跃机动的两种情况，本文提出的制导律都能够保证视线角速度和滑模面快速收敛到零。

图2(c)和3(c)给出了目标两种机动情况下参数c1,c2,c3的估计值，可以看出参数c1,c2,c3能够被估计，并且估计值cˆ1,cˆ2,cˆ3分别收敛到常值。

图2(d)和3(d)为导弹自动驾驶仪输出的制导指令的变化曲线，从中可以看出，针对余弦和阶跃两种目标机动情况，由于在设计的制导律(29)式中考虑了输入受限约束条件，制导指令值是小于最大制导指令40g的，这说明所设计的制导律有很好的控制能力。另外，在所设计的制导律下，制导指令变化连续，不存在抖振现象，且随着视线角速度趋于零的同时其响应逐渐变小直至趋于零附近。

由表1、图2(e)-2(f)和图3(e)-3(f)可见，在余弦机动和阶跃机动两种不同目标机动情况下，本文所提出的带有输入受限和自动驾驶仪的制导律都能够保证导弹有效击中目标，并且有较高的制导精度。

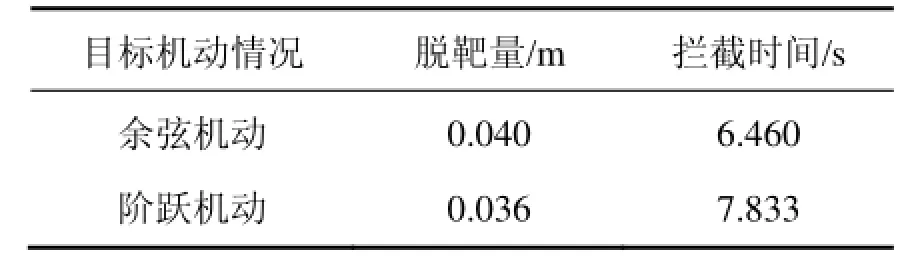
表1 两种目标机动情况下的脱靶量和拦截时间Tab.1 Miss distances and interception times of two target maneuvering cases

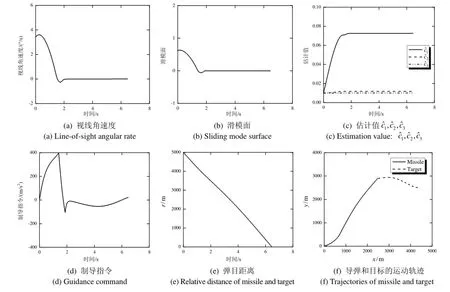
图2 针对余弦机动的仿真结果Fig.2 Simulation results for consine maneuvering

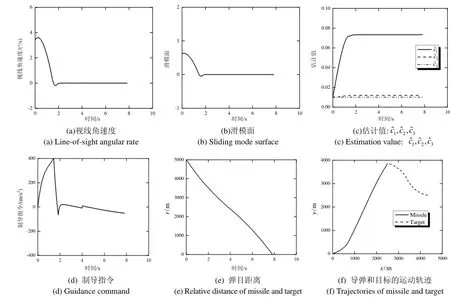
图3 针对阶跃机动的仿真结果Fig.3 Simulation results for step maneuvering

4 结 论

本文针对导弹拦截机动目标的末制导问题，基于考虑输入受限和导弹自动驾驶仪的制导模型，设计了一种新型的自适应滑模制导律。设计过程中把目标加速度视做未知有界的外界干扰，采用自适应控制算法估计干扰的上界，同时结合滑模控制，得到考虑输入受限和自动驾驶仪的自适应滑模制导律，实现了在满足输入受限约束条件下对目标机动的鲁棒性，并基于Lyapunov稳定性理论证明了该制导律的渐进稳定性。针对不同的目标机动情况，仿真结果验证了所设计制导律的有效性。

（References）：

[1] Zhang Z X, Li S H, Luo S, et al. Composite guidance laws based on sliding mode control with impact angle constraints and autopilot lag[J]. Transactions of the Institute of Measurement and Control, 2013, 35(6): 764-776.

[2] Sun S, Zhou D, Hou W T, et al. A guidance law with finite time convergence accounting for autopilot lag[J]. Aerospace Science and Technology, 2013, 25: 132-137.

[3] 刁兆师, 单家元. 考虑自动驾驶仪动态特性的含攻击角约束的反演递推制导律[J]. 宇航学报, 2014, 35(7): 818-826.

Diao Zhao-shi, Shan Jia-yuan. Back-stepping guidance law with autopilot lag for attack angle constrained trajectories[J]. Journal of Astronautics, 2014, 35(7): 818-826.

[4] 孙胜, 周荻. 考虑导弹自动驾驶仪动特性的三维非线性导引律[J]. 宇航学报, 2009, 30(3): 1052-1056.

Sun Sheng, Zhou Di. Three-dimensional nonlinear guidance law with consideration of autopilot dynamics[J]. Journal of Astronautics, 2009, 30(3): 1052-1056.

[5] 曲萍萍, 周荻. 考虑导弹自动驾驶仪二阶动态特性的导引律[J]. 系统工程与电子技术, 2011, 33(10): 2263-2267.

Qu Ping-ping, Zhou Di. Guidance law incorporating second-order dynamics of missile autopilots[J]. Systems Engineering and Electronics, 2011, 33(10): 2263-2267.

[6] Chen R H, Speyer J L, Lianos D, et al. Optimal intercept missile guidance strategies with autopilot lag[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(7): 1264-1272.

[7] Xin M, Balakrishnan S N, Ohlmeyer E J, et al. Integrated guidance and control of missiles withDθ-method[J]. IEEE Transactions on Control Systems Technology, 2006, 14(22): 981-992.

[8] No T S, Cochran J E, Kim E G, et al. Bank-to-turn guidance law using Lyapunov function and nonzero effort miss[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(2): 255-260.

[9] Zhu Z, Xia Y Q, Fu M Y, et al. Adaptive sliding mode control for attitude stabilization with actuator saturation [J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4898-4907.

[10] Xiao B, Hu Q L. Adaptive sliding mode fault tolerant attitude tracking control for flexible spacecraft under actuator actuator saturation[J]. IEEE Transactions on Control Systems Technology, 2012, 20(6): 1605-1612.

[11] Sun H B, li S H, Sun C Y, et al. Adaptive fault-tolerant controller design for airbreathing hypersonic vehicle with input saturation[J]. Journal of Systems Engineering and Electronics, 2013, 24(3): 488-499.

[12] 黄春庆, 施颂椒. 输入受限机器人的鲁棒自适应输出反馈跟踪控制[J]. 控制与决策, 2004, 19(5): 565-569.

Huang Chun-qing, Shi Song-jiao. Robust-adaptive output-tracking control of robot manipulators under input constraints[J]. Control and Decision, 2004, 19(5): 565-569.

[13] Amir T, Amin A A, Ali K, et al. Design of three-dimensional missile guidance law via sliding mode with saturation constraint[J]. Electrical and Electronic Systems, 2013, 2(1): 1-6.

[14] Shieh C S. Design of three-dimensional missile guidance law via tunable nonlinearH∞control with saturation constraint[J]. IET Control Theory application, 2009, 26(6): 697-700.

[15] 周慧波, 宋申民, 刘海坤, 等. 具有攻击角约束的非奇异终端滑模导引律设计[J]. 中国惯性技术学报, 2014, 22(5): 606-611.

Zhou Hui-bo, Song Shen-min, Liu Hai-kun, et al. Nonsingular terminal sliding mode guidance law with impact angle constraint[J]. Journal of Chinese Inertial Technology, 2014, 22(5): 606-611.

[16] Xia Y, Zhu Z, Fu M, et al. Attitude tracking of rigid spacecraft with bounded disturbances[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 647-659.

[17] Zhurbal A, Idan M. Effect of estimation on the performance of an integrated missile guidance and control system[J]. IEEE Transactions on Aerospace and Electronic systems, 2011, 47(4): 2690-2708.

Adaptive sliding mode guidance law with input constraints and autopilot lag

SONG Jun-hong, SONG Shen-min
(Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China)

In order to realize high-precision guidance when a missile intercepts a maneuvering target under the input constraints, a guidance model under input constraints is proposed based on the first-order dynamics of missile autopilot. Regarding the target acceleration as unknown bounded external disturbance, the adaptive control is designed to estimate the upper bound of the disturbance in such a way that it is not required to be known in advance. An adaptive control is designed to estimate the upper bound of the disturbance to avoid knowing it in advance. Combined with the sliding mode control, a new adaptive sliding mode guidance law with autopilot lag and input constraints is designed. Based on the Lyapunov stability theory, it is proved that the states of guidance system asymptotically converge to zero. Then, simulations on intercepting targets with consine maneuvering and with step maneuvering are made, respectively, by the proposed guidance law, and the results show that the miss distances are 0.040 m and 0.036 m, respectively, and the interception times are 6.460 s and 7.833 s, respectively.

guidance law; autopilot lag; input constraints; adaptive control; sliding mode control

V448.133

A

1005-6734(2015)03-0339-06

10.13695/j.cnki.12-1222/o3.2015.03.011

2015-01-15；

2015-05-08

航空科学基金（20140177002）；上海航天科技创新基金（SAST201402）；国家自然科学基金创新群体项目（61021002）

宋俊红（1987—），女，博士研究生。E-mail：hitsjh@163.com

联 系 人：宋申民（1968—），男，教授，博士生导师，研究方向为非线性系统的稳定性分析、鲁棒控制、导弹制导与飞行器控制。E-mail：songshenmin@hit.edu.cn