基于递推最小二乘估计的CNS/INS组合导航系统初始对准

周凌峰，赵小明，赵 帅，姚 琪，杨 琳

基于递推最小二乘估计的CNS/INS组合导航系统初始对准

周凌峰1,2，赵小明1,2，赵 帅2，姚 琪2，杨 琳2

（1. 哈尔滨工程大学 自动化学院，哈尔滨 150001；2. 天津航海仪器研究所，天津 300131）

针对CNS/INS组合导航系统中缩短初始对准时间的问题，设计了一种CNS/INS组合导航系统组合对准新方法。在CNS/INS姿态四元数组合算法的基础上，推导CNS/INS组合系统线性化状态方程，分析了INS和CNS姿态四元数差值构建量测方程。利用递推最小二乘原理实现了对该组合系统的信息融合，设计了基于该估计原理的组合导航系统初始对准方法，考虑到大气层内动基座条件下对于星敏感器造成的干扰因素增加了加权处理环节，最后通过仿真实验验证了递推加权最小二乘法在处理组合导航系统初始对准中的有效性。仿真结果表明在微晃基座条件下，与传统的滤波方法相比较该估计方法能够有效地缩短约25%的对准时间。

CNS/INS组合导航；星敏感器；初始对准；递推最小二乘

随着大视场天文导航技术的更新发展，以星敏感器为代表的天文导航设备其独立自主特点和不随时间误差积累的优势，成为了重要的辅助导航手段。近年来不少学者和工程技术人员在基于星敏感器的CNS/INS组合导航技术方面进行了大量的理论分析和工程实际研究，并在空天探测领域中取得了较为广泛的运用。文献[1]考虑了不同观星条件下CNS/INS组合的可行性；文献[2]为避免复杂非线性滤波运算针对旋转四元数建模的非线性问题，分析了基于加性四元数的CNS/INS姿态组合算法；在CNS/INS姿态匹配算法方面，文献[3]～[5]讨论了星敏感器安装误差的估计方法，以及根据组合导航系统模型利用星敏感器观测量估计惯性导航系统元件的常值误差项等。在对星敏感器安装误差的估计过程中，有学者针对工程上星敏感器安装误差高精度快速标定的需求，采用的最小二乘法推导的标定算法，取得了较好的实际效果[6]。本文考虑星敏感器在大气层内的动态使用条件，根据递推最小二乘法的原理，设计了基于星敏感器为测量器件的CNS/INS组合导航快速对准方法。

在CNS/INS组合导航系统中的初始对准方法中，比较常见的初始对准方法采用卡尔曼滤波器进行数据融合的方式，认为星敏感器的天文导航精度足够高，将其输出的姿态四元数理解为真值，视INS输出的姿态四元数为估计值，由此建立导航系统的状态方程。这种传统的方法在建立状态方程时假设了星敏感器的姿态四元数是没有受到大气层环境及载体动态环境干扰的条件的理想值，但实际情况中星敏感器处于大气层内外不同使用环境中时受到的干扰因素差别较大，可能将导致组合导航系统的姿态误差滤波收敛时间较长，有的情况甚至发散。本文提出的基于递推最小二乘估计的组合对准方法中，形式上类似于卡尔曼滤波器，根据递推回归原理，通过加权处理环节，实现对星敏感器观测量权值分析，使得组合导航系统在满足精度的条件下，实现快速对准。

1 星敏感器坐标系与导航坐标系关系

基于星敏感器技术的CNS设备，其导航原理是以恒星为参照物，利用摄像探测单元对天空进行拍摄直接捕获星图，经过数据处理单元对星图进行星图识别、质点提取、星图跟踪等一系列的计算，确定出星体跟踪器光轴在惯性空间的瞬时指向。它不需要任何外部信息自主地确定运载体相对于惯性空间的姿态；通过外部提供水平基准信息或地理位置信息，可相应地确定运载体的地理位置或载体姿态[6]。CNS的工作原理如图1所示。

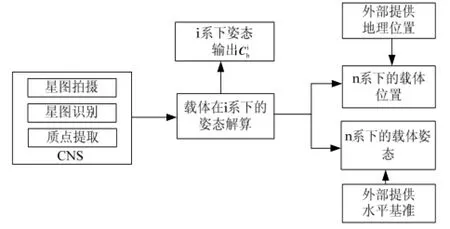
图1 CNS工作原理图Fig.1 Principle of CNS

CNS的安装误差在安装时可通过光学方法标定出来，即认为从星敏感器坐标系（s系）到载体坐标系（b系）的转换矩阵在CNS安装的时候已确定[7]。假设s系、b系基本重合，安装误差为小角度θs（θs=(θsx,θsy,θsz)），则有

其中s()×θ为各元素组成的叉乘反对称阵，即

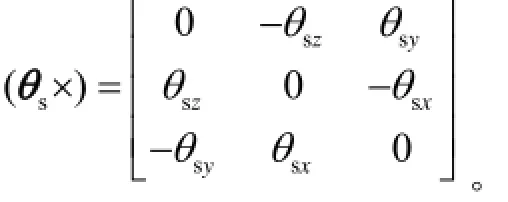
CNS通过星图拍摄、星图识别、质点提取和导航解算等一系列的计算之后，可得到星光矢量r在天球坐标系下的投影ri=(lx,ly,lz)T以及在星敏感器像空间的投影rs=(hx,hy,hz)T，两者之间的关系如下：

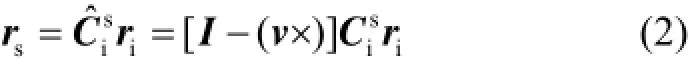
其中，v为星敏感器系统本身的测量误差，可考虑为零均值的白噪声过程。

由式(2)可知，如果能同时观测至少三颗星体，就可唯一确定坐标转换矩阵，而目前随着大视场星体快速检测技术的发展，天文导航设备已经完全具备在某一刻完成多颗星的同步检测的能力[2]。

进一步由坐标转换矩阵之间的关系，可得到载体坐标系（b系）到惯性坐标系（i系）的转换矩阵：

通过前面的分析可知，理论上CNS可在不需要任何外部先验信息条件下即可确定载体坐标系（b系）到惯性系（i系）的姿态转换矩阵。矩阵间的转换关系有

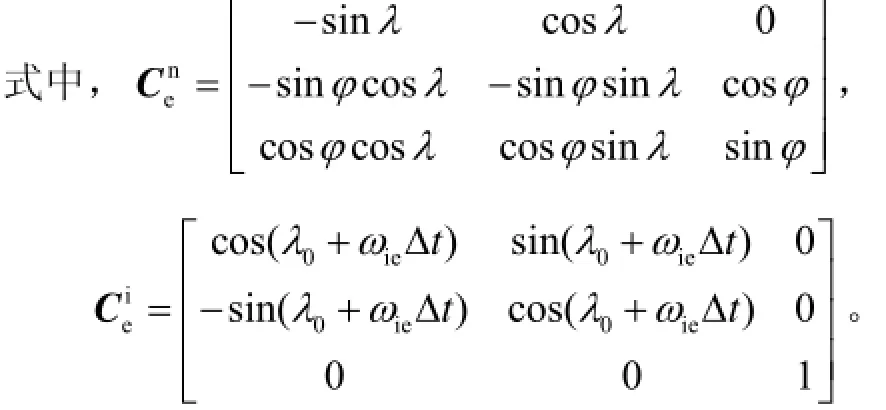
由式(4)分析可知，当CNS能获取外部提供的水平基准信息或地理位置信息时，相应地可计算得到载体位置矩阵或姿态矩阵，最后推算出载体的经、纬度值或n系下的姿态角。

INS的惯性测量单元（IMU）中，正交安装三个

其中，(,)φλ为载体的地理位置，0λ为初始经度，tΔ可由星敏感器自身携带的世界标准时间系统准确得到。敏感载体角速度的激光陀螺仪和三个敏感线加速度的加速度计。加速度计测得载体沿坐标系各轴向的加速度分量，利用陀螺测得的角速度信息计算出姿态矩阵并提取姿态角，利用姿态矩阵将加速度计的测量信息变换到导航坐标系上，然后在导航坐标系中进行加速度到速度的积分以及速度到位置的积分。INS解算的机械编排原理如图2所示。

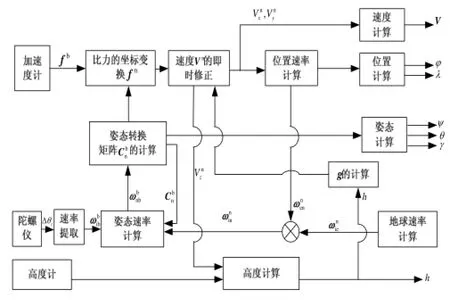
图2 INS工作示意图Fig.2 Principle of INS

INS实际输出的姿态转换矩阵为Cn′，与计算导航

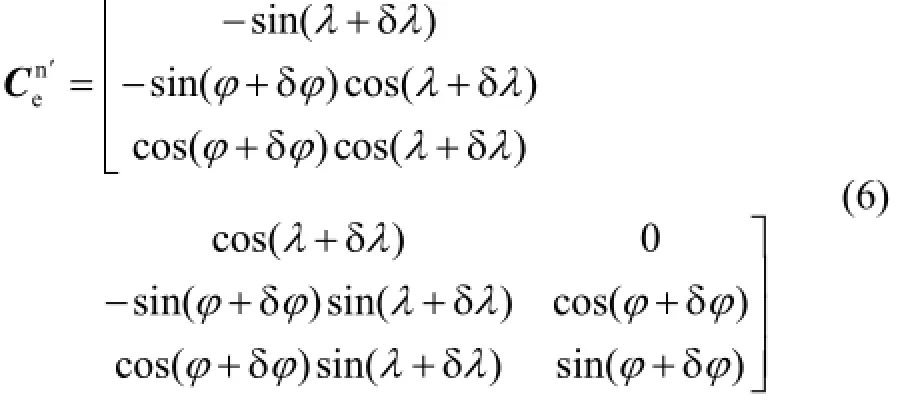
若要将INS、CNS的输出信息进行融合，首先必须将两者的输出信息统一到同一坐标系下（如i系）。根据矩阵变换之间的关系，式(7)可将INS的输出信息转换到i系：

2 CNS/INS组合导航系统对准方法

将CNS与INS进行组合，利用CNS惯性系下高精度的姿态信息辅助INS进行对准，实现组合导航系统快速对准的目的。在组合数据处理过程中，本文采用的是递推最小二乘估计器的方式进行数据融合的。

2.1递推最小二乘拟合

当应用典型的最小二乘法时，测量信息建立的方程联立如下：

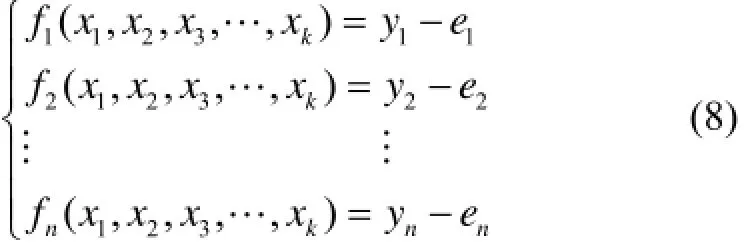
其中：x1,x2,…xk是要估计的“k”个参数；y1,y2,…,yk是n次观测；e1,e2,…,en是n次观测的误差。实现这些参数的“最佳”估计，即选用x1,x2,…xk的值，使得最小。

函数关系认为能够线性化，则有

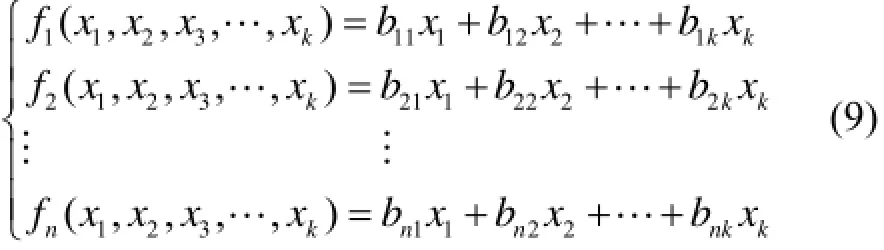
联立式(8)由可得

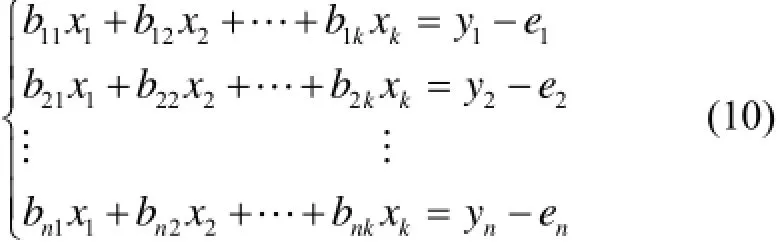
其中n≥k 。式(10)改为矩阵形式为

其中：

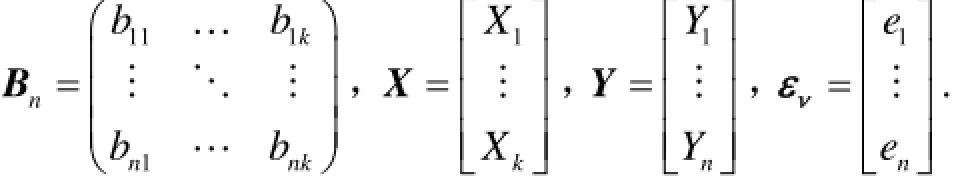
为了得到X的最小二乘估计，令

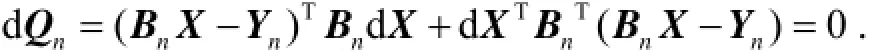
假设多进行一次观测，则有：Mn+1X=yn+1-en+1。对于状态量X用ˆn+1表示的估计值可由式(12)给出：

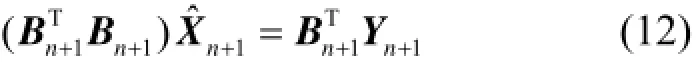
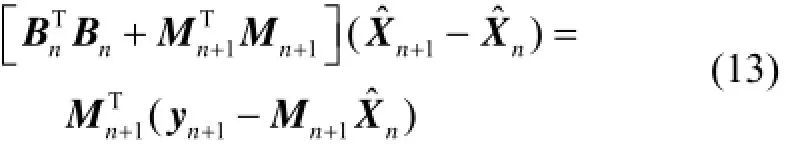
为避免在引入新观测量时出现kk×的矩阵求逆，

应用Sherman-Morisson和Bartlett公式，令

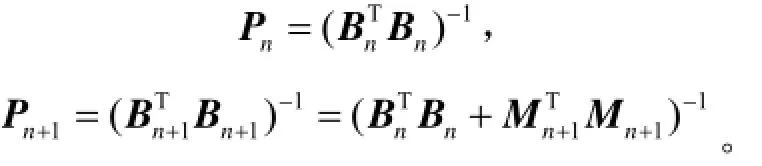
可得

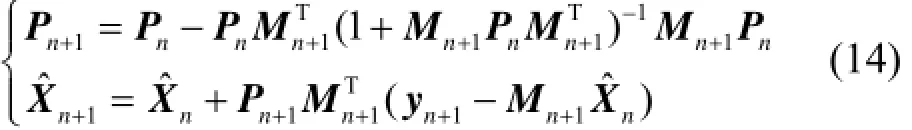
2.2加权处理

在2.1节的基础上，增加测量信息的权值分析处理环节，可以在动态干扰条件下避免CNS/INS组合系统中测量噪声带来的滤波振荡现象.考虑在测量值进行权值处理，即期望nQ最小。

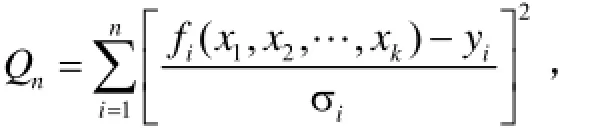
由式(12)可得

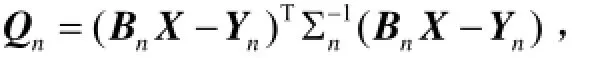
当利用加权值得到额外的信息时，有

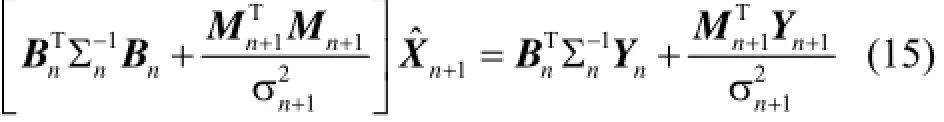
利用式(14)得到

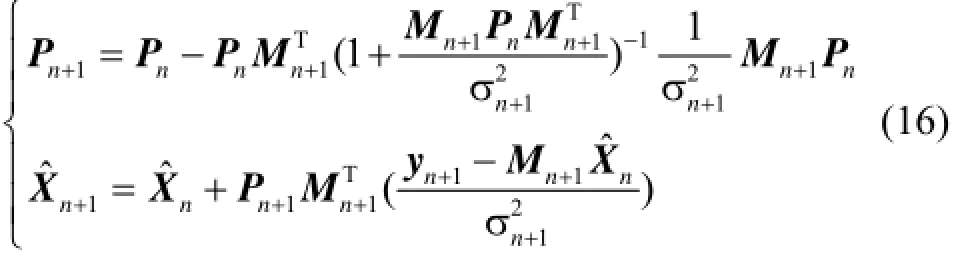
2.3组合系统初始对准流程

建立CNS/INS组合导航系统的状态方程。CNS/INS组合系统的状态方程采用INS的误差方程，方程如下：

式中，系统状态变量的具体定义为

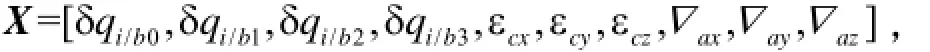
其中：δqi/b为姿态四元数真值与估计值之间的误差；εcx,εcy,εcz为陀螺随机常值误差；∇ax,∇ay,∇az为加速度计常值零位误差。

建立CNS/INS组合系统的量测方程。若直接利用CNS和INS解算出来的姿态矩阵对应元素相减作为量测量，建立的量测方程维数较高，计算相对较为复杂。根据姿态矩阵与姿态四元数q=[q q q q]i/b0123对应的关系

可求出CNS和INS相应的四元数值。假设CNS解算的惯性系下姿态四元数为/ibq˜，INS解算出惯性系下的姿态四元数为/ˆibq[2,8]，由于CNS解算的作为外参考信息，因此将CNS和INS惯性系下的姿态四元数误差作为量测值，建立量测方程为

CNS/INS组合对准的工作流程如图3所示。

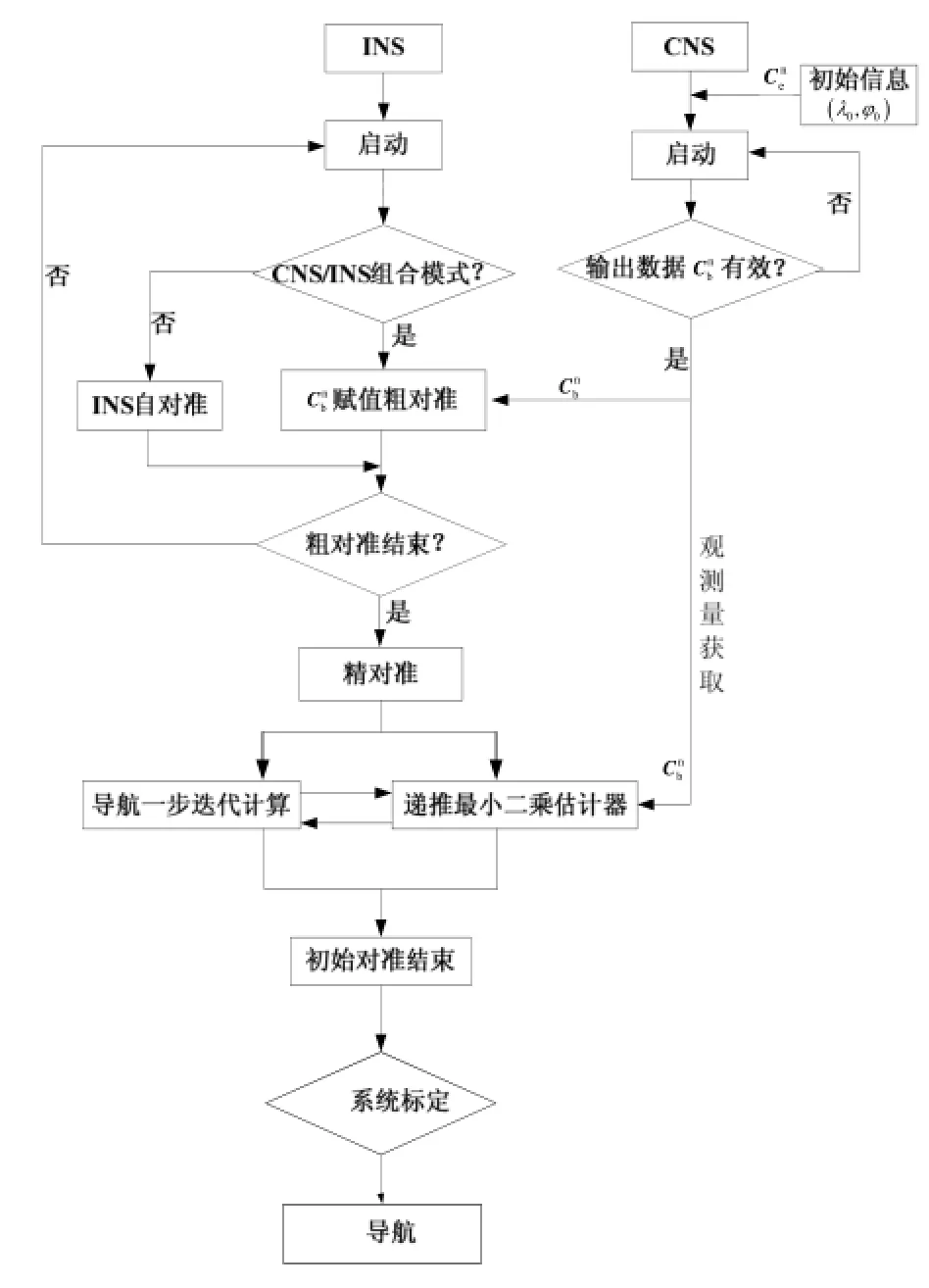
图3 CNS/INS组合对准的工作流程图Fig.3 Flowchart of initial alignment for CNS/INS navigation system

3 仿真分析

为了对比分析说明递推加权最小二乘法在处理组合导航系统中的特点，分别模拟静态下和系泊状态下的舰船姿态环境，利用传统的卡尔曼滤波方法与之比较，选取中高精度惯组作为仿真对象。系统方案采用正反停转的调制方式，水平陀螺采用中精度的陀螺，其陀螺漂移的零偏重复性为0.004 (°)/h，稳定性0.006 (°)/h；方位陀螺采用高精度陀螺，其零偏重复性优于0.0007 (°)/h，稳定性优于0.001 (°)/h；加速度计的分辨率为5×10-6g，加表零偏稳定性优于1×10-5g；惯性元件的输出频率为400 Hz，星敏感器的输出频率为1 Hz。星敏感器姿态计算方法采用QUEST算法[9]，在静态下设星敏感器的噪声为5″，可将星敏感器的测量误差考虑为均值为零的白噪声[10]。为了更好地比较仿真结果，同时为了方便观察其误差关系，将状态向量的四元数误差关系，导入地理坐标系利用水平姿态、航向误差关系来表示误差大小。

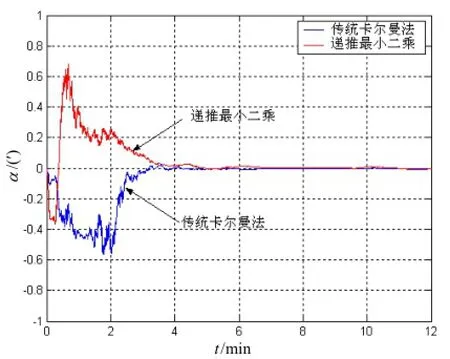
图4 静态下横摇误差对比Fig.4 Static roll errors

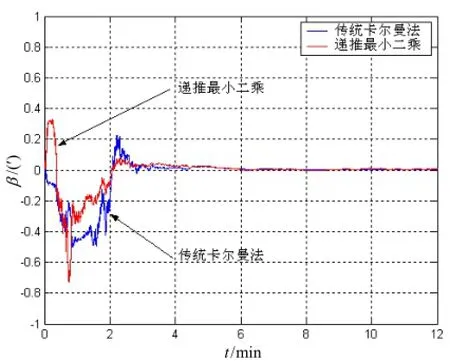
图5 静态下纵摇误差对比Fig.5 Static pitch errors

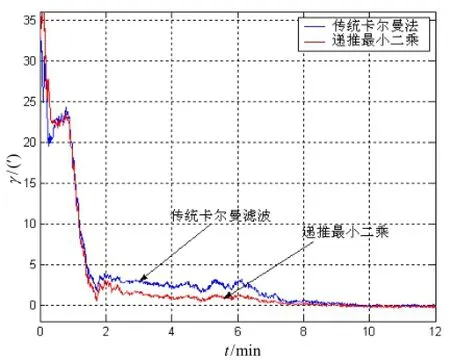
图6 静态下航向误差对比Fig.6 Static heading errors

两种方法在静态下的仿真没有明显的差别，无论是卡尔曼滤波还是递推最小二乘估计器均能在较短时间内收敛至稳定。收敛后稳态误差的峰峰值振幅小于1′，说明递推最小二乘估计能够实现对组合系统初始对准的功能，同时在较短时间内都能够满足静态对准精度要求。

假设在系泊状态下，舰船的摇摆姿态如下：航向角、纵摇角、横摇角的周期和幅值变化分别为40′、35′、50′，周期分别为10 s、8 s、8 s。考虑在大气层内晃动条件下星敏感器的杂光处理能力将受到影响，其星敏感器姿态精度用一阶马尔科夫过程表示，输出噪声为45″，相关时间为130 s。对比两种方法对初始对准精度和收敛时间的影响如图7～9。

从误差收敛的曲线可以看出，组合系统在系泊状态下，通过40 min的滤波时间无论是卡尔曼滤波方法还是递推最小二乘方法都能够估计出INS的初始对准误差来。对比二者的误差曲线从收敛时间来看，递推加权最小二乘估计器所用的时间更短，说明在系泊的晃动条件下，递推加权最小二乘估计器有较好的适应性。

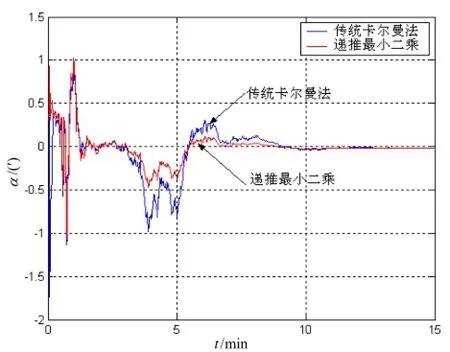
图7 动态下横摇误差对比Fig.7 Dynamic roll errors

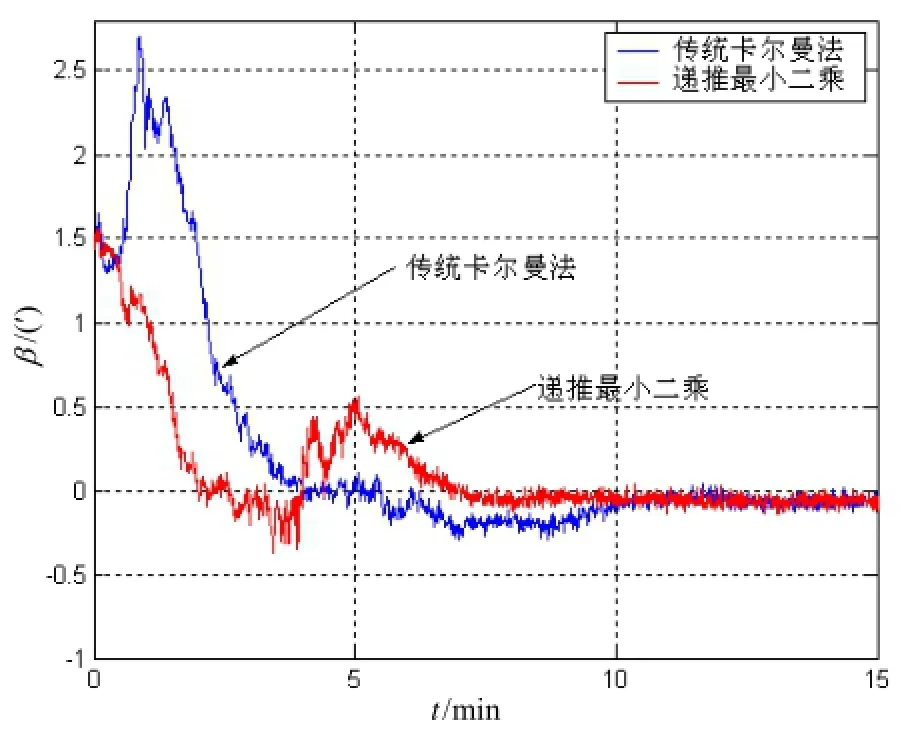
图8 动态下纵摇误差对比Fig.8 Dynamic pitch errors

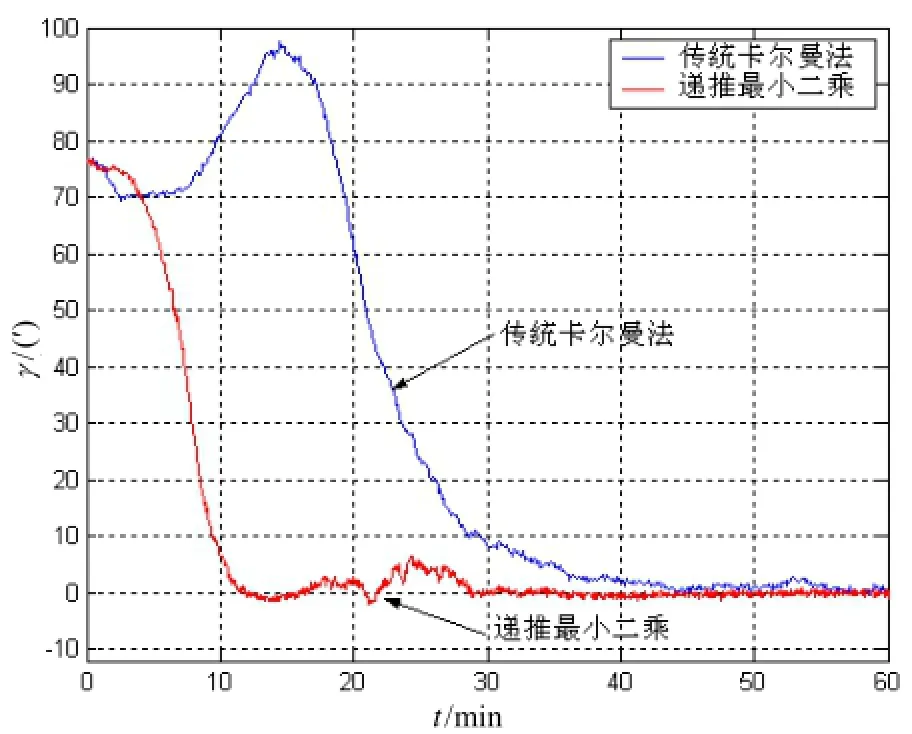
图9 动态下航向误差对比Fig.9 Dynamic heading errors

4 结 论

针对CNS/INS组合导航系统的特点，以四元数运动学微分方程为基础，以CNS和INS姿态四元数误差为观测量，联立系统的量测方程。在组合导航系统初始对准中提出了利用递推最小二乘法估计惯性导航系统初始失调角，通过加权处理的方式，增加了递推最小二乘法计算的鲁棒性，使得能够采用递推最小二乘法实现CNS/INS的初始对准过程。分别通过静态和系泊条件的数学仿真验证了其算法的有效性。当动态条件下CNS定姿精度下降时，递推最小二乘法有较强的适应能力，相对于传统的卡尔曼滤波器能够缩短25%的对准时间。虽然在仿真条件下验证了该方法的有效性，但是尝试在工程实际中应用需要对CNS/INS组合系统模型进一步的深入研究，提高算法的可靠性。

（Reference）

[1] 熊智, 刘建业, 郁丰, 等. 基于天文角度观测的机载CNS/INS组合滤波算法研究[J]. 宇航学报, 2010, 31(2): 397-403.

Xiong Zhi, Liu Jian-ye, Yu Feng, et al. Research of airborne CNS/INS integrated filtering algorithm base on celestial angle observation[J]. Journal of Astronautics, 2010, 31(2): 397-403.

[2] 屈蔷, 刘建业, 熊智. 基于加性四元数误差方程的CNS/INS姿态组合算法[J]. 中国惯性技术学报, 2011, 19(3): 316-319.

Qu Qiang, Liu Jian-ye, Xiong Zhi. Inertial/Celestial attitude integrated algorithm based on additive quaternion [J]. Journal of Chinese Inertial Technology, 2011, 31(2): 316-319.

[3] 龙瑞, 秦永元, 夏家和. 一种新的SINS/星敏感器组合导航姿态匹配算法[J]. 西北工业大学学报, 2011, 29(3): 476-479.

Long Rui, Qin Yong-yuan, Xia Jia-he. A new and effective algorithm of attitude matching for SINS/Star sensor integrated navigation system[J]. Journal of North western Polytechnical University, 2011, 29(3): 476-479.

[4] Lam Q M, Crassidis J L. Precision attitude determination using a multiple model adaptive estimation scheme[C]// 2007 IEEE Aerospace Conference. 2007: 1-20.

[5] Stuart R G. Applications of complex analysis to celestial navigation[J]. Navigation, Journal of the Institute of Navigation, 2009, 56(4): 221-227.

[6] Hu H D, Huang X L. SCNS/INS/GPS integrated navigation algorithm based on UKF[J]. Journal of systems Engineering and Electronics, 2010, 21(1): 102- 109.

[7] Wu X, Wang X L, A SINS/CNS tightly integrated navigation method based on mathematical horizon reference[J]. Aircraft Engineering and aerospace Technology, 2011, 83(1): 26-34.

[8] 张金亮, 秦永元, 吴枫. 捷联惯导基于星体跟踪器的高精度初始对准算法[J]. 中国惯性技术学报, 2013, 12(1): 22-25.

Zhang Jin-liang, Qin Yong-yuan, Wu Feng. Precise SINS initial alignment algorithm based on star tracker[J]. Journal of Chinese Inertial Technology, 2013, 12(1): 22-25.

[9] Quan Wei, Fang Jian-cheng, Xu Fan, et al. Hybrid simulation system study of SCNS/INS integrated navigation[J]. IEEE Aerospace & Electronic Systems Magazine, February, 2008: 17-24.

[10] Hua Bing, Yuan Jing, Liu Hai-ying, et al. Distributed attitude transfer alignment research based on INS/CNS integrated navigation system[C]//Proceedings of the 33rdChinese Control Conference. Nanjing, China, 2014.

Initial alignment of CNS/INS integrated navigation system based on recursive least square method

ZHOU Ling-feng1,2, ZHAO Xiao-ming1,2, ZHAO Shuai2, YAO Qi2, YANG Lin2
(1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

In order to reduce the initial alignment time of INS, a new integrated alignment algorithm is designed for CNS/INS integrated navigation system. Based on an attitude quaternion algorithm, the linear state equation of CNS/INS system is deduced, and the measurement equation is formed from the attitude quaternion errors between INS and CNS. By using a recursive least square method, the CNS/INS system’s integrated alignment data fusion is realized. A weighted average method is added when fusing the INS and CNS’s information, taking into consideration the interference factors on moving base under aerosphere. At last, the validity of using recursive weighted least square method for data fusion is testified by simulation experiments, and the results shows that the initial alignment time is reduced by 25% compared with that of the traditional Kalman filter algorithm.

CNS/INS integrated navigation; star sensor; initial alignment; recursive least square method

U666.1

A

1005-6734(2015)03-0281-06

10.13695/j.cnki.12-1222/o3.2015.03.001

2015-01-21；

2015-05-09

国家重大科学仪器设备开发专项（2013YQ310799）

周凌峰（1981—），女，博士研究生，主要从事导航、组合导航与系统控制研究。E-mail：zfl_325@sina.com

联 系 人：赵小明（1961—），男，研究员，博士生导师，主要从事导航、制导与控制系统研究。

��编号：1005-6734(2015)03-0287-06 doi: 10.13695/j.cnki.12-1222/o3.2015.03.002