新型无陀螺捷联惯导系统导航方案设计及建模
李成刚,谢志红,尤晶晶,夏玉辉,魏学东
新型无陀螺捷联惯导系统导航方案设计及建模
李成刚1,谢志红1,尤晶晶2,夏玉辉1,魏学东3
(1. 南京航空航天大学 机电学院,南京 210016;2. 南京林业大学 机械电子工程学院,南京 210037;3. 中航工业自控所 惯性技术航空科技重点实验室,西安 710065)
针对传统无陀螺捷联惯导系统角速度求解复杂,解算效率低,惯性元件安装精度要求高等问题,提出一种新型的无陀螺捷联惯导导航方案,将8-UPS型并联式六维加速度传感器作为其惯性元件,直接测量出运载体的六维绝对加速度。基于矢量力学理论,推导了其惯导基本方程;通过数值积分运算来提取载体的线运动参量;运用空间几何理论建立姿态方程,实时更新捷联矩阵以获取载体的角运动参量,从而完成了导航建模与解算。仿真结果表明该系统能满足航行体中精度实时导航的要求,是有效可行的。与同类导航相比,该系统具有结构紧凑、解算效率高、物理模型误差敏感性低等优势。
无陀螺捷联惯导;六维加速度传感器;导航解算;惯导基本方程;姿态更新
随着飞机、导弹、潜艇及机器人技术的现代化发展,捷联惯导技术成为其向快、准、稳方向发展的关键技术。无陀螺捷联惯导系统(gyro-free strapdown inertial navigation system,GFSINS)由于摒弃了结构复杂,维护困难的陀螺,因而具有结构简单、成本低廉、使用方便,可靠性高等特征,继而成为导航研究的新热点[1]。
目前国内外对传统GFSINS的研究主要集中于利用多个线加速度计的空间位置组合来代替陀螺测量载体的角运动参量[2]。Tan等提出6加速度计立方体配置构型,将6个加速度计安装于立方体各个面上,敏感轴方向沿面对角线[3],该方案结构简单,但解算出的角速度误差严重积累。对此,Park等在立方体质心处增加3个加速度计,构成9加速度计冗余配置方案[4],欲对角速度进行修正,实验证明该方案可有效抑制角速度的误差发散,但质心处设计对安装精度要求较高。随后,杨杰提出一种12加速度计平面构型方案[5],其中6个加速度计沿弹体圆截面切向,6个加速度计垂直于圆截面,以尽可能减小安装误差,提高解耦精度,但其稳定性尚待验证。此外,在实际工程应用中,传统基于加速度计组合的GFSINS还存在单轴加速度计横向灵敏度高、动态误差大、算法效率低等问题。
惯性导航的求解,本质上是对载体六维加速度的求解,因而若能结合六维加速度传感器的最新研究成果,将其应用于惯导领域中,则能为当前的无陀螺捷联惯导研究提供一种新思路。
尤等提出一种9-SPS型并联式六维加速度传感器并在其解耦算法与标定方面做了大量工作[6],研究表明该类型加速度传感器具有结构紧凑,工作频带宽,无横向灵敏度,测量范围广等优点。Xia等在此基础上研究了并联式六维加速度传感器的构型对传感特性的影响[7],发现8-UPS构型最具精度优势。本文将该8-UPS型并联式六维加速度传感器引入GFSINS中充当惯性元件,构成一种新型的无陀螺捷联惯导系统,并对其导航解算方法展开了详细研究,以解决传统GFSINS角速度求解复杂、解算效率低的问题。
1 新型GFSINS工作原理
1.1六维加速度传感器的传感原理
8-UPS型并联式六维加速度传感器以冗余并联机构为弹性体,压电陶瓷为敏感元件,通过压电陶瓷的输出信号实现对载体六维加速度的测量,其物理模型如图1所示。一个立方体质量块通过8条支链与一个盒状支撑外壳相连。8条支链分为三组,每组支链两两正交。每条支链均由1个柔性胡克铰(U)、一个移动副(P,压电陶瓷充当)和一个柔性球铰(S)串联而成,其中U铰链端与质量块相连,S铰链端与外壳相连。为便于计算与安装,每组支链的U铰链端均设计成多重复合胡克铰链,并安装于质量块的三个顶点处,安装点与质量块质心构成正四面体。
传感器工作时,其外壳底板与载体刚性固接,传感器跟随载体在惯性空间内做六维加速运动。此时,传感器外壳的运动加速度即为载体的六维加速度,被视为传感器系统的输入信号。在惯性力和惯性力矩的作用下,质量块压缩或拉伸8条UPS支链。由于压电陶瓷两端与铰链相连,各支链可视为二力杆,压电陶瓷受力后产生轴向的伸缩变形。基于正压电效应,压电陶瓷在其极化方向上产生等效电荷。将8组压电陶瓷产生的电荷搜集并经电荷放大器处理得到电压模拟量,以此作为传感器的输出信号,供计算机分析处理。
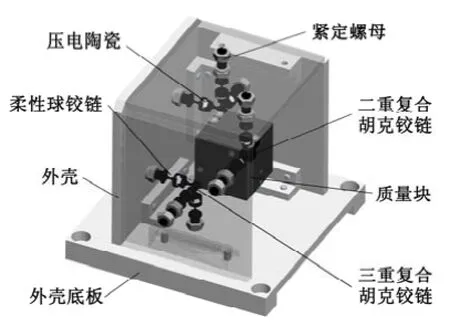
图1 新型GFSINS的惯性元件三维模型图Fig.1 3D model of the new GFSINS’s inertial element
8-UPS型并联式六维加速度传感器的求解流程如图2所示,随后对其进行详细的运动学与动力学分析。
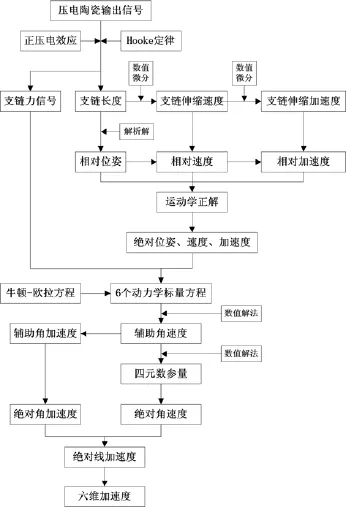
图2 8-UPS型六维加速度传感器的算法流程图Fig.2 Algorithm flowchart of 8-UPS six-axis accelerometer
1.2运动学模型
8-UPS型并联式六维加速度传感器的结构简图如图3所示。图3中,空心圆圈表示弹性球铰链,空心正方形表示复合胡克铰链。
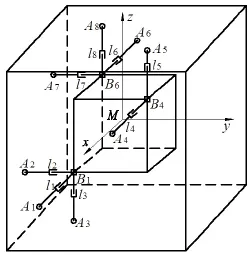
图3 新型GFSINS的惯性元件结构简图Fig.3 Structure of the new GFSINS’s inertial elements
记质量块质量为m,边长为2a,8条支链初始长度为L,分别在质量块、外壳及恒定地面上建立坐标系{M}、{S}、{O},初始时刻三者重合且坐标原点(M,S,O)位于质量块质心处,坐标轴分别平行于质量块的三条正交棱边。为避免与下文导航解算部分的绝对惯性系{I}混淆,本文将传感器中建立的惯性系{O}称为相对惯性系。
设某时刻传感器各支链长度变化量的广义坐标为ΔL,各支链上压电陶瓷输出的电压信号广义坐标为U,根据正压电效应与Hooke定律建立传感器输出坐标U与支链变形量ΔL间的关系为其中:μ表示电荷电压转换系数,tn和r分别表示压电陶瓷的厚度与半径,表示压电陶瓷极化方向的弹性柔顺系数,d33表示其极化方向压电系数。

根据空间几何知识,已知质量块上非共线3点的坐标即可求得质量块质心的空间位姿。类似地,基于四面体原理可求取质量块上3个铰链点B1、B4、B6相对于外壳系{S}的坐标。
在四面体B1-A1A2A3中,三个球铰链点在外壳{S}中的初始位置矢量SpA1、SpA2、SpA3分别为则支链长度li可表示为
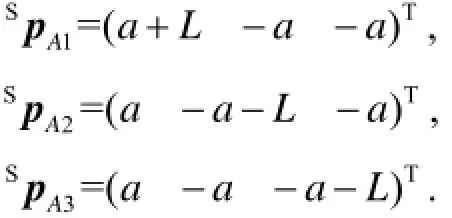
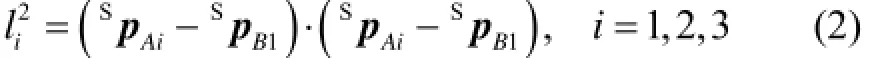
文中:CD表示运动矢量,上标{C}表示参考坐
E标系,下标{E}表示被描述坐标系,D为描述对象;ABR表示方位矩阵,上下标含义与前者相同。
由此可得三重复合胡克铰链点B1相对于外壳系{S}的位置矢量为
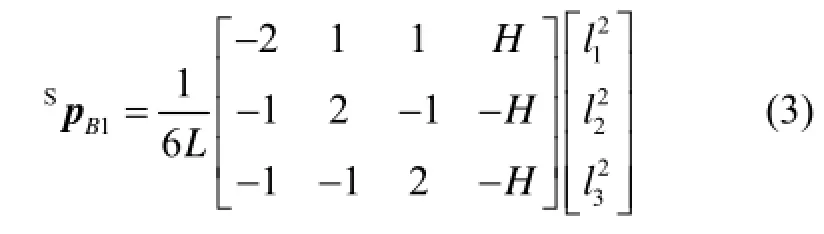
其中,H=2L2+6aL-,
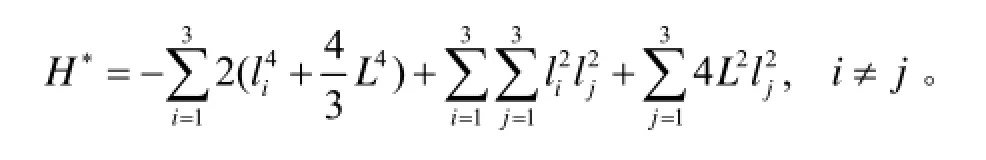
分别对矢量SpB1进行一阶和二阶时间求导,得铰链点B1相对于外壳系{S}的速度和加速度矢量分别为
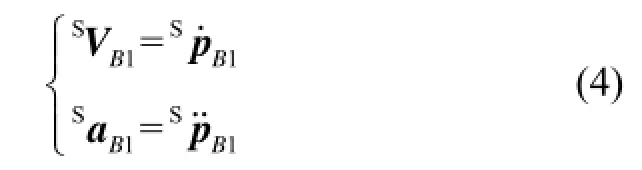
由于传感器实际应用时,支链长度的变化特性只能依靠数据采集获得的离散信号得到,因而式(4)采用数值微分法进行。
同样方法可求得铰链点B4、B6相对于外壳系{S}的位置、速度和加速度矢量。
结合第4个四面体M-B1B4B6,可得质量块{M}相对于外壳{S}的位置矢量SpM和旋转矩阵MSR分别为
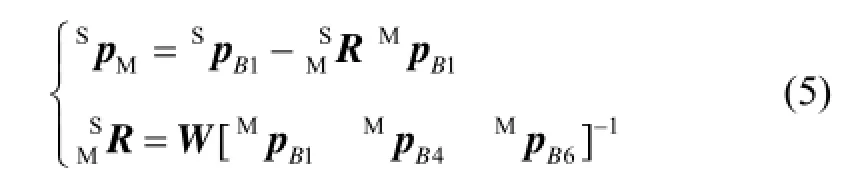
对式(5)进行一次微分、二次微分后,可得质量块{M}相对于外壳{S}的线速度、线加速度、角速度、角加速度矢量分别为
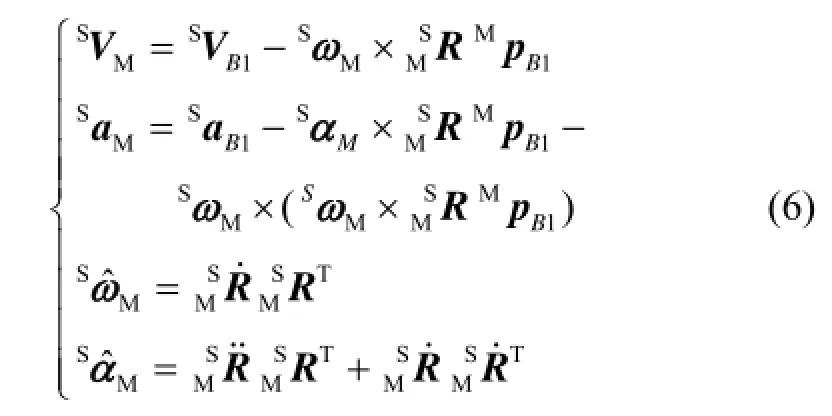
文中,ˆq表示对应矢量q的反对称矩阵。
用四元数描述物体角运动,单位四元数可表示为
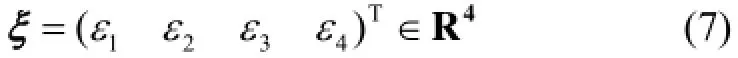
式中,ε1,ε2,ε3,ε4∈R,且有ξTξ=1。
传感器外壳{S}相对于相对惯性系{O}的旋转矩阵OSR以及角速度矢量OωS可用齐次形式表示为
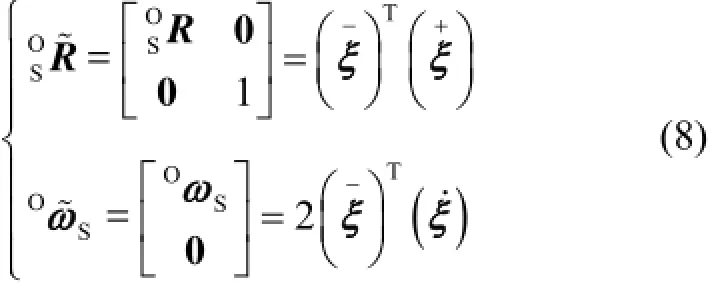
由矢量代数易知质量块{M}相对于相对惯性系{O}的绝对运动角速度和角加速度矢量分别为
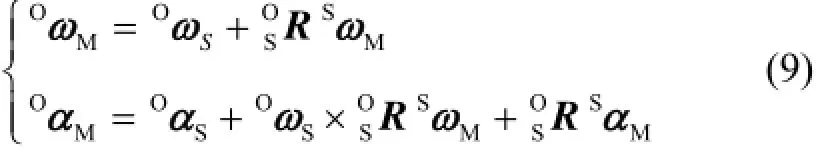
质量块{M}相对于相对惯性系{O}的位置矢量、速度矢量、加速度矢量分别为
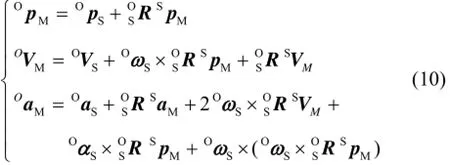
1.3 动力学模型
基于数据采集卡第i个通道采集到的电压值Ui,对应第i条支链的轴向力fi为

传感器工作过程中第i条支链的长度可表示为

质量块所受的外力包括沿8条支链轴向的压缩(拉伸)力及自身重力,其合力F以及对质量块质心的合力矩T分别为
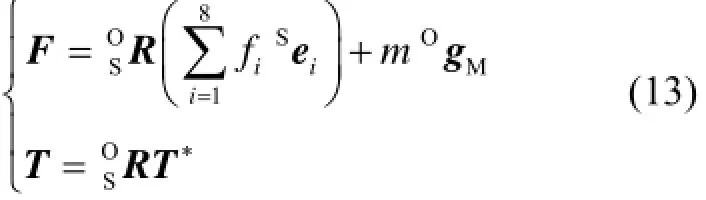
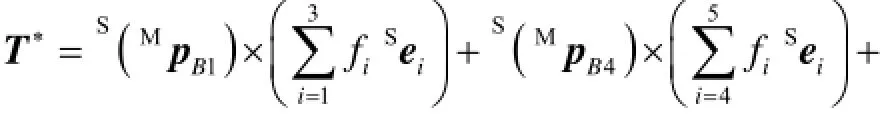
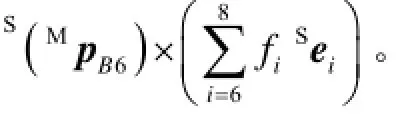
根据牛顿-欧拉法,建立8-UPS型六维加速度传感器系统的动力学方程为
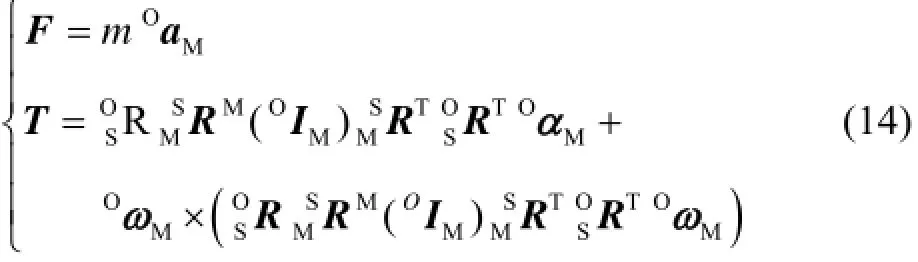
式中,M(OI)表示质量块质心相对于相对惯性系{O}M的惯性张量在质量块坐标系{M}中的表示,该参量与质量块本身的结构参数有关,为定量。
将式(9)、(10)、(13)、(14)整理可得传感器系统的两组动力学方程分别为
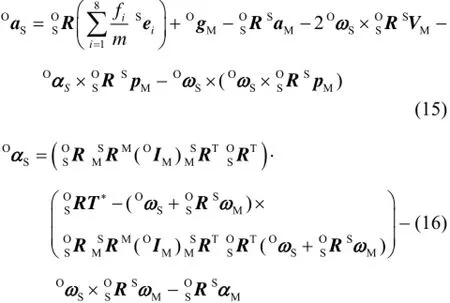
1.4解耦算法
式(15)、(16)均为高度耦合的二阶非线性微分方程组,直接对其求解比较困难。现引入辅助角速度*ω,使其满足关系式[8]对上式两边进行微分,得

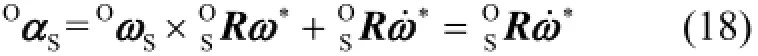
将式(17)、(18)代入式(16)可将其化简为只包含*ω和*ω˙的一阶非定常线性微分方程组:
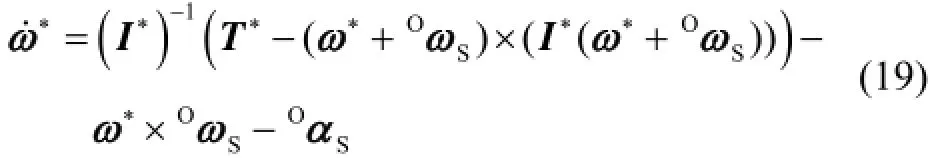
对式(19)采用改进的欧拉算法进行求解,可得传感器任意时刻的辅助角速度*ω和角加速度*ω˙。联立式(8)、(17)可得

该方程为一阶非定常线性微分方程。同样采用改进的欧拉算法递推得到传感器任意时刻外壳{S}相对于相对惯性系{O}的旋转四元数参量ξ及其导数˙。
由于数值计算会引入误差,使得四元数不满足关系式T1=ξξ,此处对四元数进行违约修正,用式确定的修正值*ξ来代替ξ:

将以上得到的传感器某时刻的ω*、ω˙*及ξ分别代入式(8)、式(17)、式(18)中,可得到任意时刻传感器外壳相对于相对惯性系{O}的旋转矩阵、角速度矢量OωS以及角加速度矢量OαS。再将得到的运动参数代入到第一组动力学方程(式(15))中即得到传感器外壳相对于相对惯性系{O}的线加速度矢量Oa。S
1.5导航工作原理
将传感器解耦出的有效参数作为惯性元件的输出,输入到导航解算系统中。由于传感器安装在载体的非质心处,因而系统进行解算时,首先要将以外壳系{S}为主体的运动参量全部转换为以载体系{B}为主体的参量,后者表征了载体的绝对运动状态。借助捷联矩阵将转换后的载体加速度投影到导航参考系中,然后代入惯导基本方程中求出导航线加速度,线加速度经一次积分即可得导航线速度。此线速度一则作为导航系统的线速度输出,二则作为导航位置求解的输入,三则输入到导航角速度方程中用于求解位置角速度。运用空间几何理论建立姿态方程,实时更新捷联矩阵,并用反三角函数求解出姿态角。新型GFSINS的导航解算流程如图4所示。
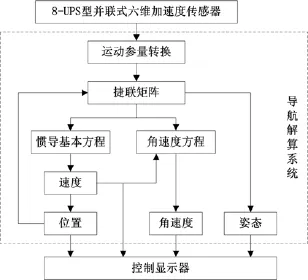
图4 GFSINS导航工作原理图Fig.4 Navigation functional principle of GFSINS
2 导航解算
导航解算需要的常用参考坐标系如图5所示。
绝对惯性系{I}:恒定不变坐标系,原点o位于地心,xI轴指向春分点,zI轴沿地球自转轴,yI轴与xI、zI轴构成右手系。
地球坐标系{E}:为载体航行提供地球参考,原点位于地心,xE轴穿越本初子午线与赤道的交点,zE轴穿越地球北极点,yE轴穿越东经90°子午线与赤道的交点。该坐标系与地球固联。
地理坐标系{G}:跟踪载体在地球表面的位置,原点位于载体质心,xG轴在当地水平面内指向东,yG轴沿当地子午线指向北,zG轴沿当地垂线指向天,又称为东北天坐标系。
载体坐标系{B}:与载体固联,用来跟踪载体的姿态,原点位于载体质心,xB轴沿载体横轴向右,yB轴沿载体纵轴向前,zB轴沿载体立轴向上。
导航坐标系{N}:导航基准坐标系,本文设导航系与地理系重合,该系统又称为指北方位系统。
在进行导航系统参数解算时,待求参数有:载体相对于地球的位置,载体相对于地球的速度在导航系{N}中的表示,载体系{B}相对于导航系{N}的姿态,以及载体系{B}相对于导航系{N}的角速度在载体系{B}中的表示。
将传感器与载体刚性固接,保证载体系{B}和外壳系{S}相互平行。此时,传感器安装位置矢量Bp为S
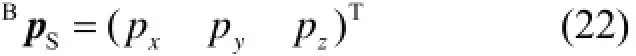
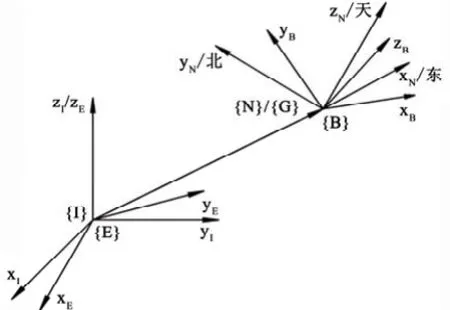
图5 导航参考坐标系示意图Fig.5 Diagram of navigation reference frames
静基座条件下,导航的初始位置及姿态记为
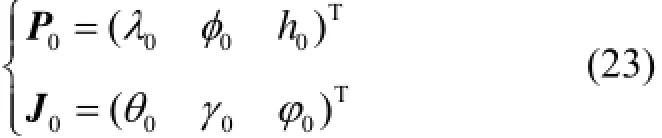
式中:λ、φ、h分别表示载体的经度、纬度、高度;θ、γ、φ分别表示载体的俯仰角、横滚角和航向角。
2.1运动参量转换
根据第1节中六维加速度传感器的各项输出参数,首先将其转换为以载体系{B}为主体的参量,如图6所示,由于传感器位置固定,载体系{B}和外壳
系{S}始终相互平行且相对静止,故有
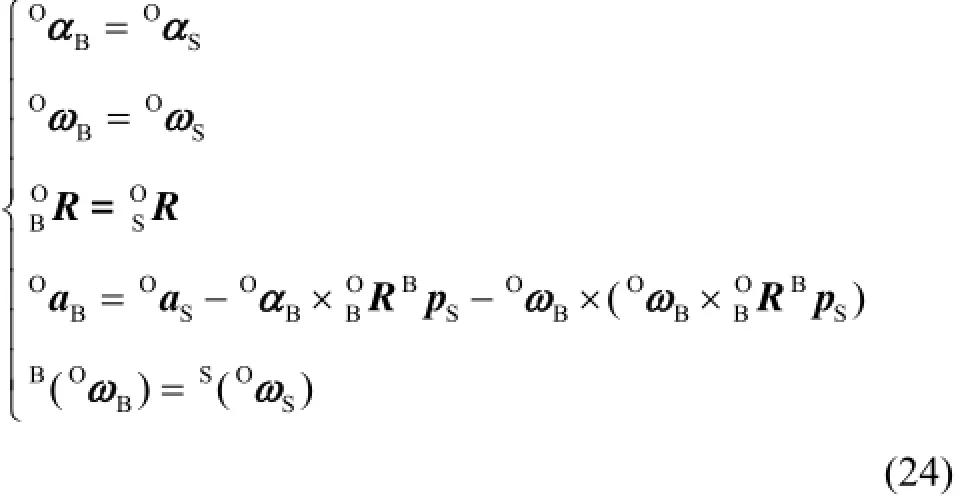
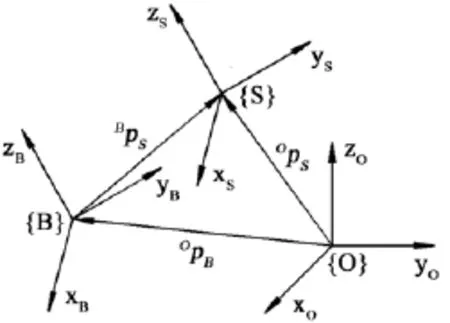
图6 载体、外壳和相对惯性坐标系间的位置关系示意图Fig.6 Position relations among the body, the shell, and the relative inertial coordinates
已知绝对惯性系{I}和相对惯性系{O}之间相差初始位姿矢量0P、0J。欲实现其相互转换,需以零时刻导航系{N0}为桥梁,先将绝对惯性系{I}经三次基本旋转后与导航系{N0}重合,再将导航系{N0}经三次基本旋转后与相对惯性系{O}重合。根据欧拉定理:
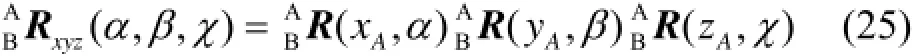

根据速度合成定理,有
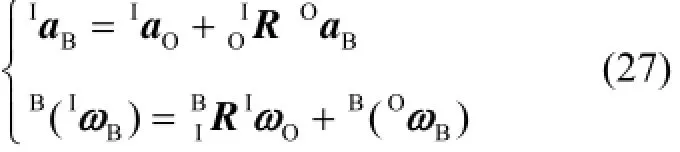
式中,IaO=0,IωO=0,且由于载体系{B}和导航系{N}原点相互重合,故有
与其他类型的捷联惯导系统相比,IaB和B(IωB)分别与线加速度计测量值和陀螺测量值相互等效。
2.2惯导基本方程
参考图5中的位置关系,根据矢量力学原理推导出导航系{N}相对于绝对惯性系{I}的位置矢量为式中,I

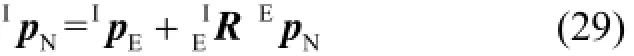
E=0p。
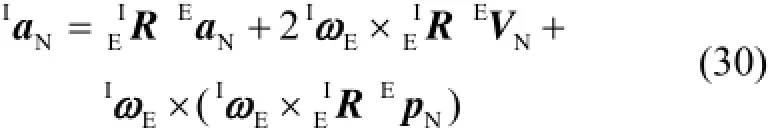
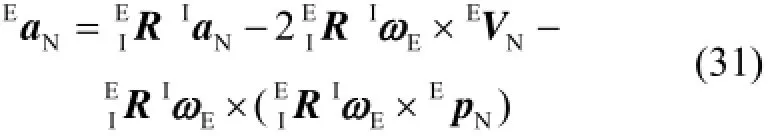
将EVN表示到导航系{N}中可得导航速度为

对式(32)两边进行微分,并联系式(30)、式(31)化简得惯导基本方程为
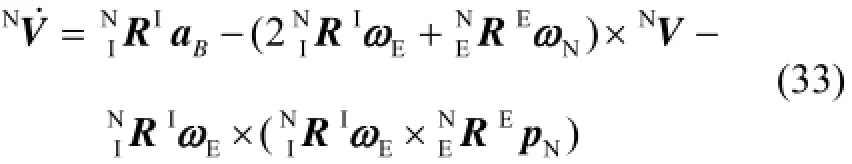
值得注意的是,与传统的单轴加速度计组合测量不同,新型惯性元件能直接测量出运载体的六维绝对加速度而非比力从而包含地球引力场的影响,避免了加速度转换过程中的重力补偿问题,进而提高了导航线运动参数解算的效率和精度。
导航速度为
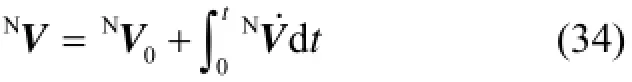
在指北方位系统中,东向速度分量引起运载体经度变化,北向速度分量引起运载体纬度变化。导航速度的直角坐标与经纬坐标转换[9]如下:表示地球半径。将导航速度进行一次积分可得导航位置
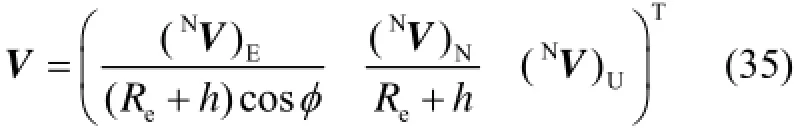

式中:
分别采用梯形法和辛普森法则[10]完成式(34)和式(36)中的数值积分运算。
最终,导航的位置和速度参数表示为
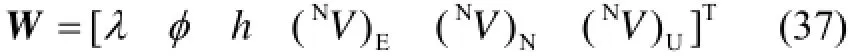
2.3导航姿态信息提取
联系式(27),由角速度加法公式求解导航角速度为
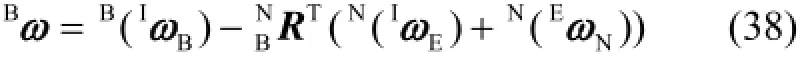
根据空间几何理论,导航姿态方程为
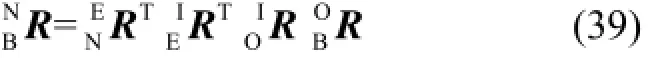
由上述两式可知,由于传感器解耦过程中能输出角运动参量,因而新型GFSINS在角速度求解和姿态更新方面变得十分简单高效,可避免涉入过多的计算误差,提高了导航角运动参数解算的效率与精度。
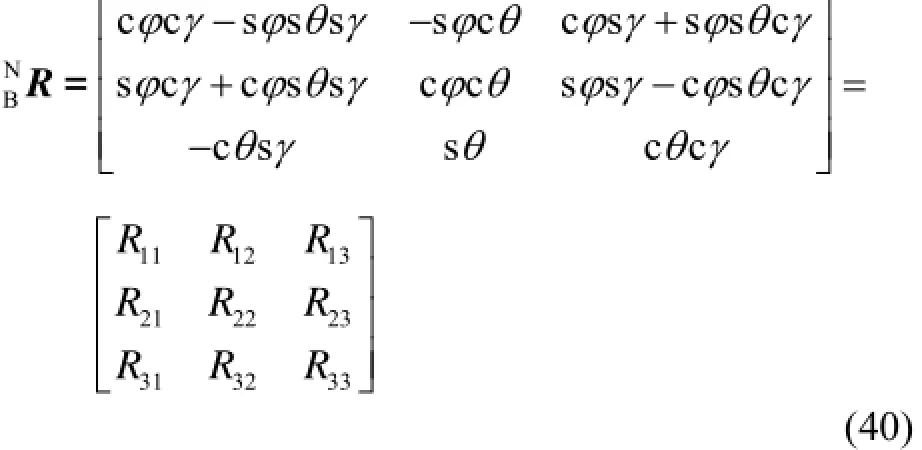
已知姿态矩阵表达式为通过反三角函数即可求解出载体姿态角为
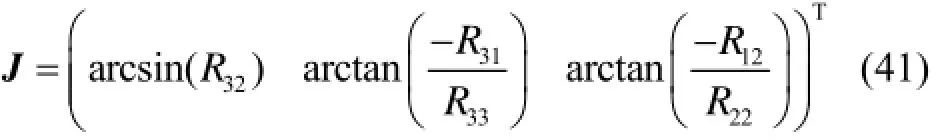
式中:J=(θγφ)T,θ∈(-π/2,π/2),γ∈(-π,π),φ∈(0,2π)。
由式(41)可知:俯仰角在定义域内正弦函数唯一,可单值确定;横滚角和航向角在定义域内正切函数不唯一,需中其他元素辅助判定,判定如表1。

表1 横滚角γ和航向角φ的真值判定表Tab.1 Determination of rollγand yawφ
3 仿真试验及分析
在计算机上对新型GFSINS进行静基座条件下的仿真分析,如图7所示,分别建立8-UPS型传感器虚拟样机模型和地球环境虚拟模型。不作特别标注时,下文涉及的线单位为mm,角单位为rad。仿真初始参数设置:=(1.047,0.349,1000)T,=(0.524,0.698,0.873)T,=(100,200,300)T。结合目前飞机、导弹等航行体的飞行量程,对载体施加具有一般性的六维驱动。

图7 计算机仿真设计图Fig.7 Simulation design by computer
仿真时间为30 s,采样频率为1000 Hz,采集传感器虚拟样机中8条支链的长度变化量,视为压电陶瓷的输出信号,借助计算机依次进行加速度解耦和导航参数解算。引入均方根误差kS来表征新型GFSINS的测量精度,如式(43)所示,并将每个参数分量误差的平均值作为参数误差,记为S。
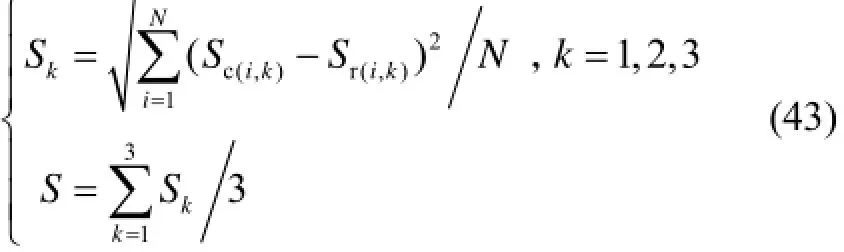
最终,导航的姿态和角速度参数表示为
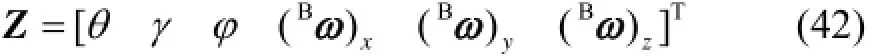
式中:N表示仿真步数;Sc、Sr分别表示参数的计算值和真值。限于篇幅,给出新型GFSINS的东向速度误差如图8所示,其他详细误差见表2。
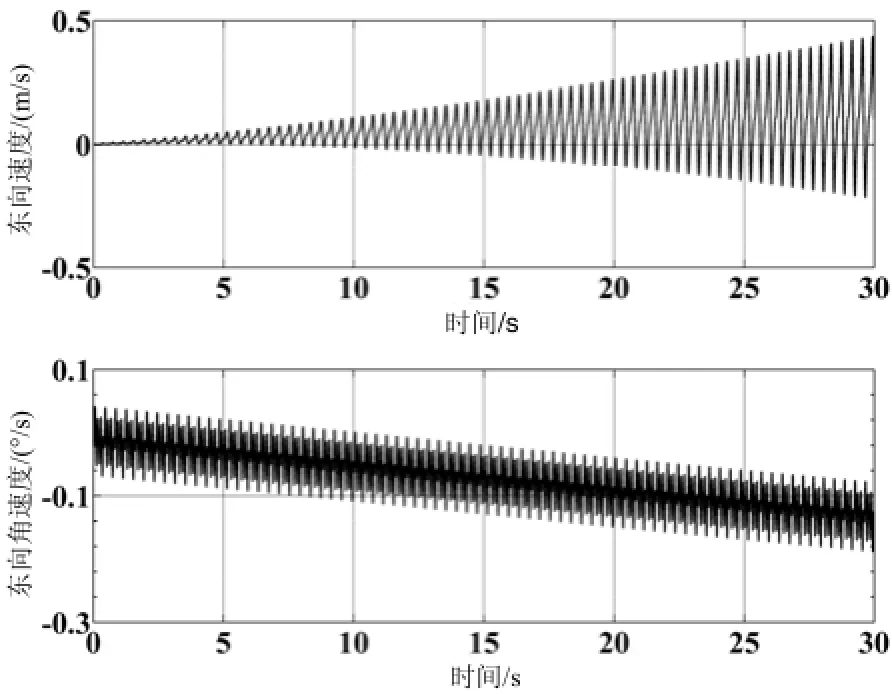
图8 新型GFSINS的导航东向速度误差Fig.8 Velocity errors of the new GFSINS in east direction
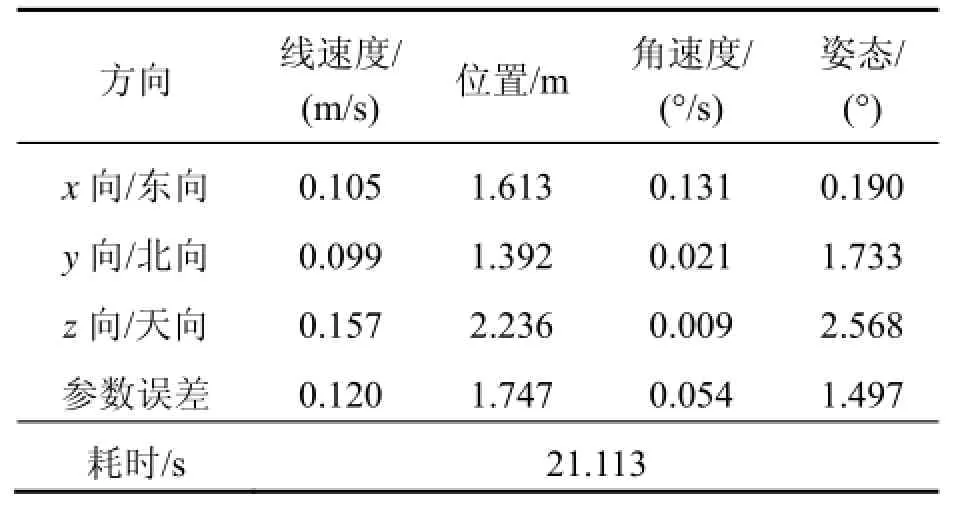
表2 新型GFSINS的导航误差Tab.2 Navigation errors of the new type of GFSINS
观察并分析图8、表2可知:①该导航系统在短时间内精度较高,30 s内的位置误差小于2 m,线速度误差小于0.2 m/s,姿态误差小于1.5°,角速度误差小于0.06 (°)/s,参数解算耗时21.113 s,说明新型GFSINS能满足载体的中精度实时导航要求,是有效可行的。②与现有的无陀螺捷联惯导系统相比,本系统对位置和速度的测量精度基本持平,但对角速度和姿态的测量精度则有明显提高,这是因为传感器在进行解耦运算时,率先求解出外壳的角运动参数;此外,导航系统解算时,对传感器输出的其他解耦变量也进行了充分利用,避免了复杂算法带来的计算误差,进而提高了导航系统的精度与效率。③由于数值计算涉入了舍入误差和截断误差,本系统存在误差积累问题,这也是所有惯导的固有缺陷,可进一步通过优化算法、组合校正等办法予以改善,对此将另文研究。
4 结 论
提出了一种基于8-UPS型并联式六维加速度传感器的新型GFSINS导航方案,以解决传统GFSINS角速度求解复杂,解算效率低的问题。利用传感器解耦得到的中间变量,建立新系统的导航数学模型,完成导航解算。基于矢量力学原理推导惯导基本方程,用六维绝对加速度代替比力从而包含地球引力场的影响,规避重力补偿问题,提高了解算精度;根据角速度加法公式建立角速度方程获取导航角速度;利用空间几何理论建立姿态方程来实时更新捷联矩阵。
仿真实验结果表明:新型GFSINS在30 s内的导航位置误差优于2 m,线速度误差优于0.2 m/s,姿态误差优于1.5°,能满足航行体的中精度实时导航需求,是有效可行的。较于目前的导航系统,新系统在算法(特别是角速度和姿态算法)的效率与精度兼顾性方面,具有很大竞争力,能够为当前的GFSINS研究提供一种新思路。
(References):
[1] Tazartes D. An historical perspective on inertial navigation systems[C]//2014 International Symposium on Inertial Sensors and Systems. 2014: 1-5.
[2] 汪小娜, 王树宗, 朱华兵, 等. 无陀螺捷联惯性导航技术[J]. 中国惯性技术学报, 2010, 18(5): 538-542.
Wang Xiao-na, Wang Shu-zong, Zhu Hua-bing, et al. Gyroscope-free strapdown inertial measurement techniques[J]. Journal of Chinese Inertial Technology, 2010, 18(5): 538-542.
[3] Tan C, Park S. Design of accelerometer-based inertial navigation system[J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(6): 2520-2530.
[4] Park S, Tan C, Park J, et al. A scheme for improving the performance of a gyroscope free inertial measurement unit[J]. Sensors and Actuators A - Physical, 2005, 121(2): 410-420.
[5] 杨杰. 无陀螺捷联惯导系统加速度计构型研究与误差分析[D]. 哈尔滨: 哈尔滨工程大学, 2011.
Yang Jie. Accelerometer configuration and error analysis for GFSINS[D]. Harbin: Harbin Engineering University, 2011.
[6] 尤晶晶, 李成刚, 吴洪涛, 等. 基于并联机构的六维加速度传感器的方案设计及建模研究[J]. 振动工程学报, 2012, 25(6): 658-666.
You Jing-jing, Li Cheng-gang, Wu Hong-tao, et al. Study on scheme design and modeling of a six-axis accelerometer based on parallel mechanism[J]. Journal of Vibration Engineering, 2012, 25(6): 658-666.
[7] Xia Yu-hui, Li Cheng-gang, You Jing-jing, et al. Influences analysis of configurations on the performance of parallel type six-axis accelerometers[J]. Transactions of FAMENA, 2013, 37(2): 67-86.
[8] 尤晶晶, 李成刚, 吴洪涛, 等. 六维加速度传感器的两类解耦算法及其对比研究[J]. 中国机械工程, 2013, 24(21): 2938-2943.
You Jing-jing, Li Cheng-gang, Wu Hong-tao, et al. Study and comparison on two decoupling algorithms of six-axis accelerometer[J]. China Mechanical Engineering, 2013, 24(21): 2938-2943.
[9] 秦永元. 惯性导航[M]. 第二版. 北京: 科学出版社, 2014.
Qin Yong-yuan. Inertial navigation[M]. 2nd ed. Beijing: Science Press, 2014.
[10] Wu D, Wang Z. Strapdown inertial navigation system algorithms based on geometric algebra[J]. Advances in Applied Clifford Algebras, 2012, 22(4): 1151-1167.
Navigation scheme design and modeling of a novel gyro-free SINS
LI Cheng-gang1, XIE Zhi-hong1, YOU Jing-jing2, XIA Yu-hui1, WEI Xue-dong3
(1. College of Mechanical and Electronic, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China; 2. College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China; 3. Aviation Key Laboratory of Science and Technology on Inertia, Flight Automatic Control Research Institute, Xi’an 710065, China)
Traditional gyro-free strapdown inertial navigation system(SINS) has such disadvantages as complicated angular velocity decoupling, inefficient navigation parameters calculation, and harsh mounting requirements of inertial sensor, etc. To solve these problems, a new type of gyro-free SINS was put forward, in which an 8-UPS six-axis accelerometer of parallel type was taken as the inertial component to measure the carrier’s absolute six-axis acceleration. The basic inertial navigation equation was derived based on the principle of vector mechanics. The carrier’s line motion parameters were extracted through numerical integration. In addition, the attitude equation was established by geometric theory to real-time update the strapdown matrix. In this way, the navigation modeling and calculating are realized. Simulation results show that the new system is feasible and effective in satisfying the real-time moderate-accuracy navigation requirements. Compared with other similar navigations, the new gyro-free SINS has such advantages as compact structure, high calculation efficiency, and low sensitivity to physical model error, etc.
gyro-free SINS; six-axis accelerometer; navigation calculation; basic inertial navigation equation; attitude update
U666.1
A
1005-6734(2015)03-0303-08
10.13695/j.cnki.12-1222/o3.2015.03.005
2015-01-06;
2015-05-06
国家自然科学基金(51175263、51405237);航空科学基金(20130852017);南京航空航天大学研究生创新基地(实验室)开放基金(kfjj201436);中央高校基本科研业务费专项基金;江苏省高校自然科学研究资助(14KJB460020)
李成刚(1975—),男,副教授,从事六维加速度传感器、惯性导航技术研究。E-mail:lichenggang@nuaa.edu.cn

