仿真转台伺服系统动态模型辨识与计算

李 慧，陈前荣，朱 震，甘 霖

仿真转台伺服系统动态模型辨识与计算

李 慧，陈前荣，朱 震，甘 霖

（中国洛阳电子装备试验中心，洛阳 471003）

仿真转台广泛应用于光电制导导引头及其对抗的仿真，对某型仿真转台进行高精度模型辨识可以有效提高系统的动态控制精度和设计效率。基于此，提出了一种转台伺服系统频率特性自动测试方法，根据测试数据采用参数递阶辨识方法分段拟合得到了被控对象的高精度传递函数模型。辨识结果与实测数据相比：在体现伺服系统重要特征的中低频段，幅度绝对误差＜1 dB，相位绝对误差＜2°；在高频段，得到了复杂的机械谐振环节特性，验证了被控对象传递函数模型的准确性。对于转台的动态精度计算，采用频率设计分析建模方法，结合被控对象高精度传递函数和实际校正环节模型得到了转台的动态精度计算模型，通过比较同一输入情况下实测动态误差与模型输出误差数据验证了模型准确性，结果表明了该方法的有效性。建立的动态精度计算模型能够反映实际系统的动态过程和动态误差变化规律，也为同类设备伺服系统的模型辨识和动态精度分析计算提供了方法。

仿真转台；动态模型；频率特性分析；递阶辨识法；模型辨识

在光电制导导引头及光电制导导引头对抗半实物仿真试验中，仿真转台广泛应用于模拟弹体姿态角运动及导引头目标之间的视线角运动，可对被试导引头的跟踪稳定等跟踪性能技术参数（隔离度、跟踪速度和跟踪精度等）进行测试[1-4]。某型仿真转台是进行高重频激光干扰装备对激光半主动导引头干扰效果半实物仿真评估试验的重要仿真设备[5]。仿真转台的动态控制误差直接影响高重频干扰激光束的实时指向精度和干扰效果评估。

对于仿真系统和仿真试验，最引人关注的问题是系统的精度如何。为保证半实物仿真试验系统得到有效应用，有必要在分析某型仿真转台的控制系统结构和动态精度分析建模的基础上，准确掌握并事先确定在半实物仿真试验中不同战情条件下转台的动态响应过程和动态误差曲线。在仿真转台伺服系统设计分析时，基于经典控制理论的对数频率综合法是最成熟的控制方法[6]。但作为频域设计分析法的基础，要求获得被控对象的传递函数。对被控对象进行高精度模型辨识可以提高转台控制系统的控制精度和设计效率[7-8]，因此开展某型仿真转台伺服系统动态模型的辨识与动态精度分析计算的研究具有重要的应用价值。

根据某型仿真转台伺服系统的构成原理，提出了一种频率特性自动测试方法，通过控制计算机产生正弦扫频信号充分激励被控对象，同时记录其输出响应。利用参数递阶辨识原理，分段拟合得到了被控对象高精度传递函数模型，并对辨识模型进行了准确性验证。对于仿真转台的动态精度计算，结合高精度被控对象传递函数模型和实际校正环节模型建立了伺服系统的闭环动态精度计算模型。对同一战情输入情况下实测的动态误差数据和模型仿真输出误差数据进行了比较，验证了动态精度计算模型的准确性，表明了该方法的有效性。

1 仿真转台伺服系统结构与频率特性自动测试原理

某型仿真转台伺服控制系统结构如图1所示。仿真计算机给出的角位置指令信号由某型仿真转台控制计算机经过伺服校正后，经由D/A转换送入驱动控制器，由电机驱动控制器放大后驱动台体作相应转动，同时测角元件测量出转轴的实时角位置，经过高速数字I/O卡输入到转台控制计算机，实现闭环控制。

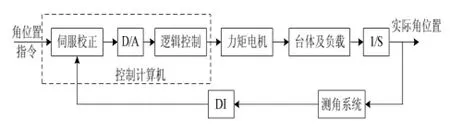
图1 转台伺服控制系统结构图Fig.1 Servo system diagram of turntable

针对转台数字化控制系统特点，被控对象（即力矩电机、台体和负载）频率特性自动测试方法如下：在测试带宽内，选取一定数量的频率测试点，首先改变输入谐波信号Xisinωt的频率ω，并采集得到与此相对应的输出幅值Xo(ω)与相移Ψ(ω)，进行数据预处理后采用相关分析或FFT等方法计算输入输出信号在每个频率点处的幅度比和相位差，然后做出幅值比Xo(ω)/Xi随频率变化的幅频特性曲线以及相移Ψ(ω)随频率变化的相频特性曲线，最后采用参数辨识法得到被控对象的精确开环传递函数。

2 仿真转台传递函数模型辨识与验证

2.1 被控对象开环频率特性测试

2.1.1 测试数据处理

某型仿真转台的俯仰框首先需要测试力矩电机的加速能力和线性度，即测试其最大角速度和角加速度是否满足指标要求，并据此得到测试转台开环频率特性时的输入正弦扫频信号的幅值。在转台处于开环状态下，由控制计算机产生一定频率范围内（1～17 Hz）的频率可调的正弦扫频电压指令信号（频率1 Hz时，幅值为3 V，其他频率时幅值为5 V），该扫频信号通过力矩电机驱动台体作正弦摆动，采集记录不同频率范围内的输入正弦扫频信号和输出角度传感器反馈的角位置数据，对得到的数据经过消除漂移和噪声的预处理后，再计算输入输出信号在每个频率点处的幅值比和相角差。

由于系统中存在各种干扰，采集的反馈数据可能会存在错误点和漂移。对于存在粗大误差点，可利用相邻前后4点的均值与该点的偏差大小来判断该数据正确与否；若偏差过大，则利用前后4点的均值代替原数据。为了消除直流漂移的影响，对测试数据进行了中值滤波，将测试数据进行平稳化处理。对于线性漂移的影响，需要进行稳态截取，去除每个频率点的前几个周期扫频数据，并将每个正弦周期拟合一条直线，然后用测试曲线将其减去后再进行幅值和相角差的计算以消除直线漂移的影响。

2.1.2 幅值比和相角差计算

幅值比和相位差的分析计算主要有两种方法：FFT谱分析法和相关分析法。两种算法各有优劣，但目的都是要计算出系统在每个频率点下的幅值比和相位差，这里是采用FFT分析法进行分析计算，进而可绘制其频率特性曲线。

经过上述处理后可得到仿真转台俯仰框实测的开环频率特性曲线。图2所示为俯仰框幅频特性曲线，图3所示为俯仰框相频特性曲线。

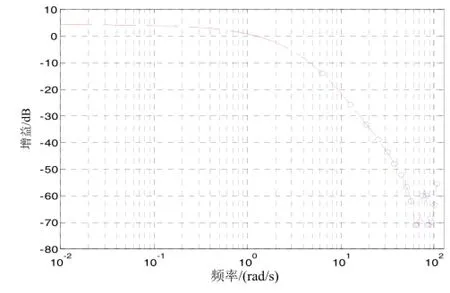
图2 俯仰框幅频特性曲线Fig.2 Magnitude-frequency response of elevation frame

图3 俯仰框相频特性曲线Fig.3 Phase-frequency response of elevation frame

2.2 被控对象模型辨识与参数估计

要获得被控对象的传递函数，可以对实测的电机对象频率特性数据进行曲线拟合。传递函数辨识实质上是寻找一个传递函数，使其频率特性与实测得到的被控对象的频率特性相同或满足某种误差最小原则。某型仿真转台系统开环调试时测量得到的只是在不同频率点上的输出与输入之间的幅值比和相角差，要将其转换为传递函数，首要的问题是给出传递函数模型的阶次。可先将测量得到的开环频率特性画出伯德图，然后根据几种典型环节及其组合（惯性环节，积分环节，二阶振荡环节等）的频率特性曲线与画出的伯德图对比来确定传递函数的阶次，但有时这样确定的阶数并不准确，因为当多个环节组合在一起时某些环节因其特性不明显可能被忽略。此时可以根据控制对象的运动机理推导得出简化的传递函数模型从而确定传递函数的阶次。当传递函数模型确定后，传递函数辨识问题便成为根据测量得到的频率特性数据来确定传递函数模型中的未知参数的曲线拟合问题。

由图2和图3俯仰框开环频率特性曲线低频段（ω＜60 rad/s）可知，被控对象可能为两个或多个惯性环节的串联，在高频段系统的幅频特性和相频特性均明显出现了异常，在ω=65 rad/s和ω=90 rad/s间，幅值和相位急剧变化，出现了谐振现象，说明对象传函中应包含一个二阶微分环节和二阶振荡环节组合而成的机械谐振双二阶环节。下面基于电机驱动负载的物理机理来确定被控对象的传递函数模型阶次。

由电机驱动负载的电枢平衡方程和力矩平衡方程可得到

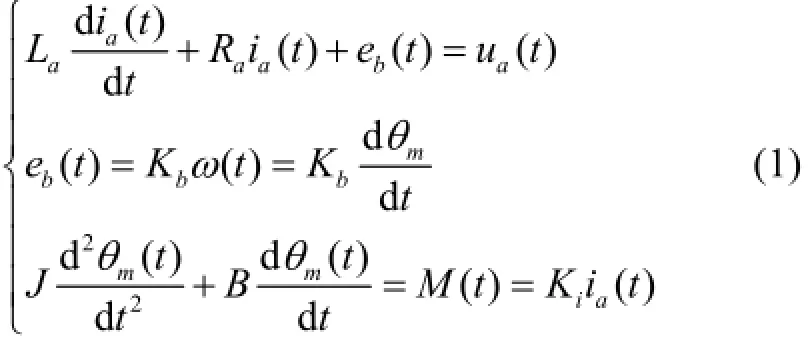
取电枢电压ua(t)为输入变量，负载转轴角位移θm(t)为输出变量的传递函数为

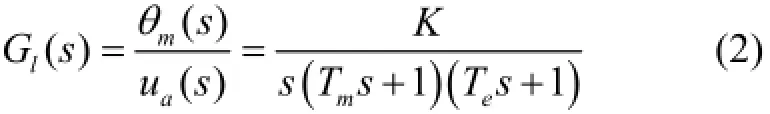
其中，K为系统增益，mT为机电时间常数，eT为电磁时间常数。

实际上由于系统的机械刚度有限，系统的开环特性通常在高频段包含一个或多个传递函数如式(3)所示的机械谐振双二阶环节：

从实测的系统开环频率特性数据和上述的理论推导分析，可以将不加补偿的某型仿真转台外两轴台俯仰框的开环传递函数模型确定为式(1)和式(3)的串联，如式(4)所示：

式中，Ghi(s)(i=1,2,…,n)表示引起机械谐振的第i个双二阶环节。此时传递函数辨识问题就简化为根据实测的系统开环频率特性数据来确定式(4)中的未知参数的曲线拟合问题。

曲线拟合的方法有最小二乘法、参数递阶辨识和Levy法等[9-11]。Levy法根据修正的误差准则，运用求极值的方法得到传递函数的参数。当被辨识对象传递函数的阶次较低时，拟合算法简单，辨识精度较高。考虑到某型仿真转台等实际系统较理想模型要复杂很多，通常存在多个谐振频率，为了准确描述其幅频特性，需对其高阶谐振进一步建模。由于参数较多，为降低计算复杂度，这里采用参数递阶辨识方法进行处理。其基本思想是按照被控对象的频率特性，将高阶系统分解为多个维数较小、参数较少的子系统，根据测量得到的频率特性数据，先辨识低频环节，得到结果后，再从得到的频率特性数据中将辨识出的低频环节修正掉，然后依次辨识高频环节，这样就可以得到完整的传递函数。

2.3 实测数据与辨识模型结果验证

对实测数据通过参数递阶辨识得到了被控对象的中低频段的传递函数为

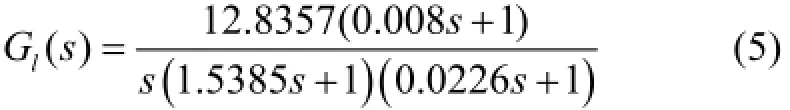
在高频段拟合时，先从图2和图3所示的被控对象频率特性曲线中修正掉已得到的式(5)所示中低频段环节的特性数据，可得到机械谐振的频率响应图，确定第一谐振模型的数据范围为9～12 Hz之间，通过拟合得到第一个双二阶环节机械谐振模型为

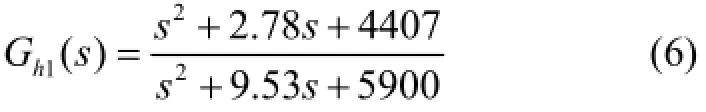
同理，在机械谐振频率响应曲线中修正掉第一个谐振模型Gh1(s)后，可得到系统中存在的另外的谐振模型为

被控对象完整的传递函数为

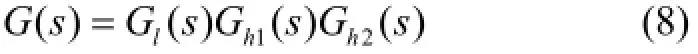
分别做出辨识得到的传递函数模型(8)的幅频特性和相频特性曲线，并与实测的开环频率特性数据进行对比，如图4和图5所示。两者之间的误差曲线如图6所示，从辨识结果可以看出：在频率为5～60 rad/s范围内时，幅频特性绝对误差＜1 dB，相频特性绝对误差＜2°，辨识精度很高；在＞60 rad/s的高频段时，由于多个机械谐振点的影响，辨识误差变大，幅频特性绝对误差＜3 dB，相角误差＜10°。

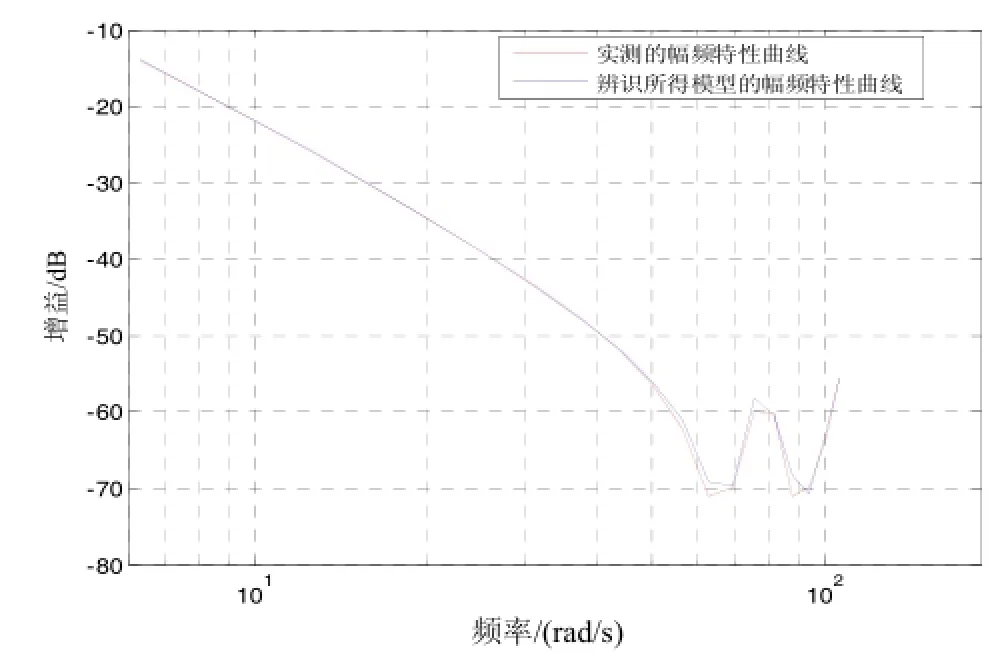
图4 实测幅频特性与辨识模型的幅频特性曲线Fig.4 Magnitude-frequency response curves of simulation and experiment

综上所述，利用参数递阶辨识原理，分段拟合方法将某型仿真转台俯仰框实测得到的频率特性数据转换为高精度的传递函数。其中在体现伺服控制系统重要特征的中低频段，幅度绝对误差＜1 dB，相位绝对误差＜2°；在高频段也将复杂的机械谐振环节拟合出来。被控对象高精度传递函数和谐振频率参数的获得使在下面的控制校正时可以对机械谐振环节进行有效的抑制，也对控制校正参数的调试获取提供了依据。

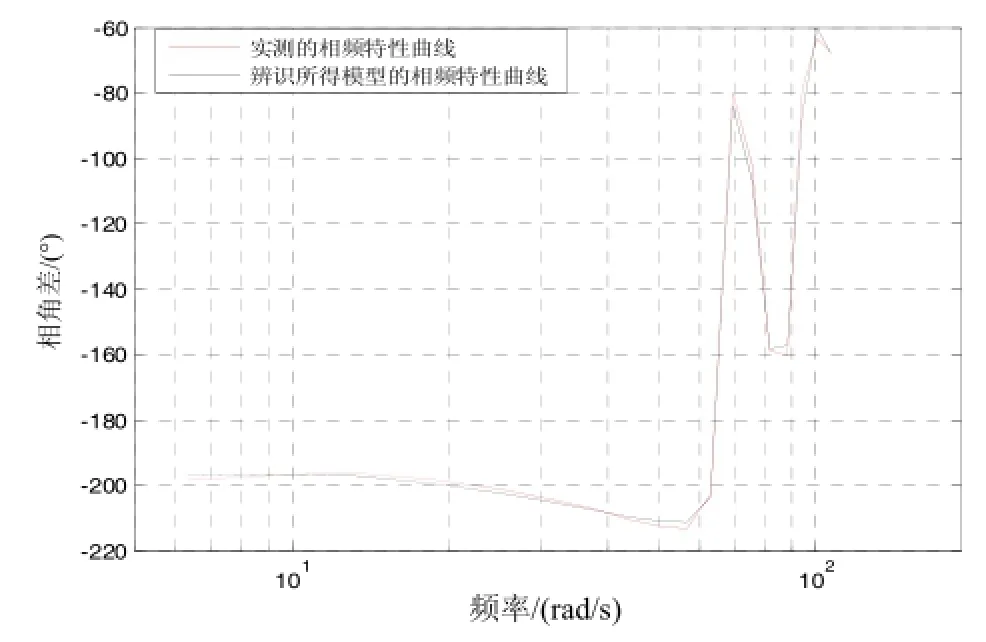
图5 实测相频特性与辨识模型的相频特性曲线Fig.5 Phase-frequency response curve of simulation and experiment

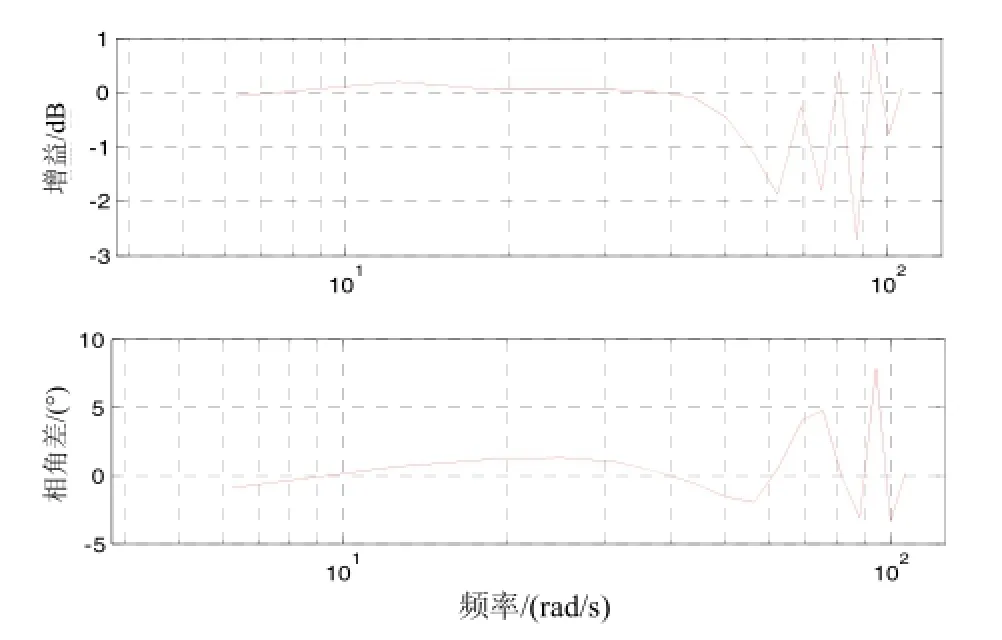
图6 辨识误差Fig.6 Residual errors

3 仿真转台动态精度建模及验证

3.1 仿真转台动态模型建立

某型仿真转台的伺服控制系统应为一快速随动系统，应能快速准确的执行上位机送来的引导指令并完成随动控制。但实际上，由于频带有限，电机的控制执行力不够，其控制系统是存在幅值衰减和相位滞后的，这是产生动态误差的主要原因。另外，还有一些扰动因素如非平衡质量、噪声、摩擦和机械谐振等也会在一定程度上影响控制误差。在光电对抗半实物仿真试验系统中，无论是仿真设备（仿真转台等）还是仿真系统的能量、视线角和光斑等主要参量模拟精度，均需要用动态模拟误差来度量。某仿真周期下的参量状态值与参量控制值一次差就是该周期下的动态模拟误差，如果能建立反映转台输入输出运动规律和动态特性的动态精度计算模型，就可以对各种战情输入情况下的动态误差进行分析计算。

工程上，对于采用经典的频域分析法设计的伺服控制系统，一般可采用动态误差系数法进行动态精度的分析计算与评价。这种方法是将系统近似简化为I型或II型系统，动态控制误差仅与输入信号以及速度、加速度误差系数有关。但是即使输入的指令信号有同样的速度、加速度，高阶导数分量的不同同样带来不同的控制误差，误差系数与伺服系统的控制结构和参数也有关，对于不同的系统可能计算误差较大。另外，进行转台动态控制精度分析的方法也可采用实践中广泛应用的过程辨识方法，即将转台动态控制过程看作“黑箱”，只考虑过程的输入输出特性，而不强调过程的内部机理，直接利用转台控制系统的输入指令信号与输出误差信号，通过递推最小二乘等方法建立其等效动态控制误差模型[12]。但这种方法对转台系统的验前知识依赖很大，即需要精确设计辨识输入信号，尽可能多的包含系统的动态信息，同时必须准确掌握系统的结构和阶次等关键参数，也要考虑实际系统执行过程的可行性，辨识计算难度较大。要获得准确的转台动态精度计算模型，这里采用了频域设计分析建模方法对其伺服系统进行设计和实际调试，确定了系统各个校正环节的参数，被控对象的高精度传递函数模型与经过调试后的校正环节模型结合，可得到其伺服控制系统的闭环动态精度计算模型。

工程上，一般采用串联校正（超前校正环节、滞后校正环节等）、反馈校正和前馈校正等方法，对机械谐振的校正可采用加入陷波滤波环节来抑制。但总的来说，频域分析校正方法是一种“试凑”设计方法，实际中可能需要几次迭代反复调试才能完成校正设计。加入前馈补偿后仿真转台伺服控制系统结构如图7所示。

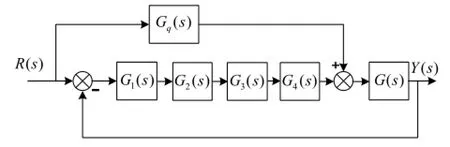
图7 加入补偿后转台伺服控制系统框图Fig.7 Servo system diagram of turntable (with adjuster)

图7中：G(s)为被控对象的传递函数；Gq(s)为前馈补偿环节传递函数，加入该环节主要为了拓展系统频带，提高系统控制精度；G1(s)、G2(s)和G3(s)等为串联校正环节传递函数，实际中可能会加入更多串联校正环节。文中以仿真转台俯仰框伺服系统实际调试完成后加入的补偿校正环节进行说明。

加入一定转角频率的一阶惯性环节G1(s)主要是为了抑制高频噪声，起到低通滤波器的作用，其传递函数为

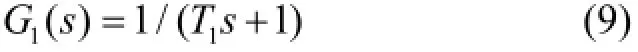
加入二阶陷波环节2()Gs是为了抑制机械谐振的影响，其传递函数为

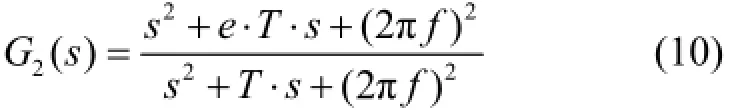
式中，f为中心频率，T用来调节陷波器的带宽，e用来调节陷波器的深度。实际调试中可能加入几个陷波环节来抑制可能存在的机械谐振点。

加入超前校正环节3()Gs用来补偿穿越频率处的相角损失，保证系统的相角稳定裕度，其传递函数为

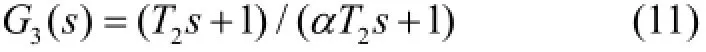
加入滞后校正环节4()Gs，加滞后环节会减小穿越频率处的幅值和相角裕度，但能提高中心频率前的增益。其传递函数为

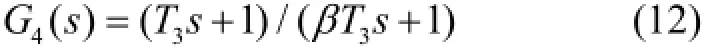
伺服控制系统补偿校正就是为了得到各个校正环节传递函数中的未知参数，利用劳斯判据分析了系统的稳定性，可满足稳定要求。

3.2 仿真转台动态模型的仿真验证

得到某型仿真转台俯仰框控制系统的闭环动态精度计算模型后，可先对该模型进行仿真验证。为验证模型准确性，根据转台的最大角速度和最大角加速度指标设计等效正弦信号或者指数、弹道目标作为输入，经过仿真分析模型对输入指令信号的动态响应和控制误差曲线，可确定模型能否反映转台的实际动态特性。

根据仿真转台最大角速度和最大角加速度指标设计等效正弦信号作为输入，为了与下节实际测试时输入的正弦指令信号一致，采用了将输入正弦信号的速度逐段逐渐达到最大，并将输入正弦信号进行了一定角度的偏置。仿真转台俯仰框动态模型的输入与输出响应曲线如图8所示，仿真转台俯仰框响应等效正弦目标输入时的动态误差曲线如图9所示。

3.3 仿真转台动态模型的实测验证

在同一输入条件下，分别对比通过实验测试得到的仿真转台俯仰框动态误差数据与转台俯仰框的动态精度分析模型仿真计算输出的动态误差数据，可对动态模型的准确性进行进一步验证。

在等效正弦信号输入下，某型仿真转台俯仰框动态误差实测值与仿真值变化如图10所示。两者在幅值上变化趋势基本一致，但是在初始段由于仿真时角度是从0°突然变化到18°左右，这个阶跃冲击造成的过渡过程与实际测试时是不一样的，实际测试时是将转台俯仰框先引导到18°左右，这样目标初始也在18°，初始段也能够稳定跟踪目标。在逐段输入正弦信号的后半段仿真输出与实际输出规律将会保持一致，但是动态精度计算模型输出在相位上滞后实际输出动态误差1/4周期左右，需要进一步分析其原因。动态精度计算模型输出误差的均值为-3.32′，标准差为4.42′，实测动态误差均值为-0.02′，标准差为3.95′。实际测试中在双十指标范围内高频信号输入下，转台俯仰框动态误差实测值与仿真计算值变化规律也基本一致。的动态模型，分析比较了在等效正弦目标输入情况下，实测的动态误差与仿真模型计算的动态误差之间的差异，结果表明两者的均值和标准差差别均在3´以内，分析结果满足系统要求。

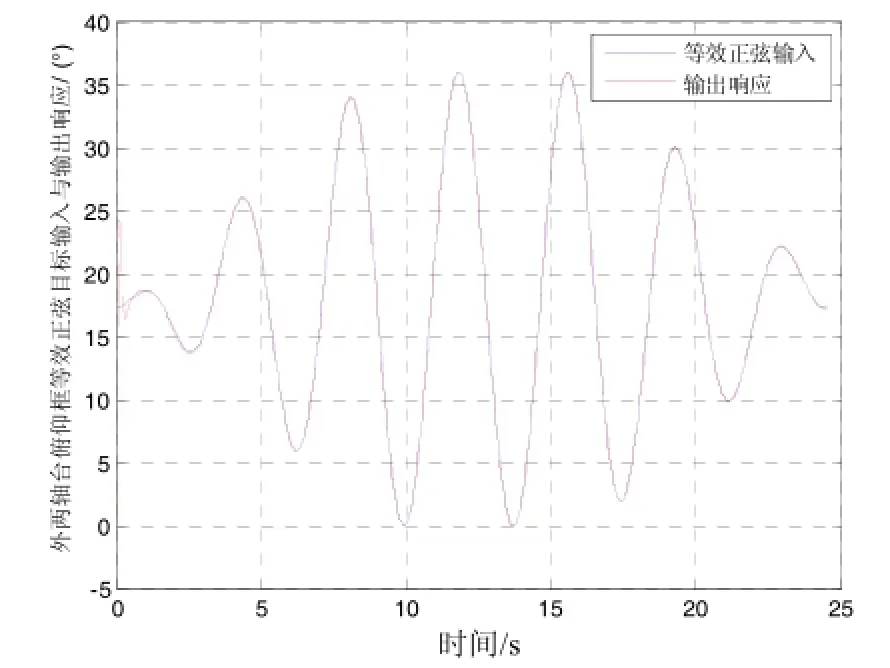
图8 转台仿真模型的等效正弦输入与输出响应Fig.8 Equivalent sine input and response of turntable dynamic model

图9 转台仿真模型的动态误差Fig.9 Dynamic error of turntable dynamic model

4 结 论

针对某型仿真转台数字化伺服系统的控制结构，提出了一种被控对象频率特性自动测试方法。利用参数递阶辨识方法得到了被控对象的高精度传递函数模型。与实测数据比较，辨识结果在体现伺服系统重要特征的中低频段，幅度绝对误差＜1 dB，相位绝对误差＜2°，在高频段也得到了复杂的机械谐振环节，在系统校正时可对机械谐振环节进行有效的抑制。

采用频率设计分析法建立了该型转台伺服系统

图10 等效正弦输入时转台动态误差实测值与模型输出值Fig.10 Simulation and experimental results of turntable dynamic error (equivalent sine input)

提出的动态模型辨识与计算方法是合理有效的。建立的动态模型能够较好反映转台系统的动态过程和动态误差变化规律，为光电导引头对抗闭环半实物仿真试验系统的精度分析提供了方法和模型支持。

（References）：

[1] Leylek E, Ward M, Costello M. Flight dynamic simulation for multibody aircraft configurations[J]. Journal of Guidance Control and Dynamics, 2012, 35(6): 1828-1839.

[2] Locke1 M, Czarnomski M, Qadir A, et al. High-performance two-axis gimbal system for free space laser communications onboard unmanned aircraft systems[C] //Free-Space Laser Communication Technologies XXIII, Proc. of SPIE. 2011, Vol.7923: 1-8.

[3] Hilkert J M, Amil D L. Structural effects and techniques in precision pointing and tracking systems - A tutorial overview[C]//Acquisition, Tracking, Pointing, and Laser Systems Technologies XXIV, Proc. of SPIE. 2010, Vol. 7696: 1-12.

[4] Li Jie. Optimization design of the precision optoelectronic tracking turntable frame[C]//5th International Symposium on Advanced Optical Manufacturing and Testing Technologies, Proc. of SPIE. 2010, Vol. 7659: 1-5.

[5] 李慧，甘霖，张文攀，等. 激光制导武器对抗半实物仿真弹干视线角模拟精度分析[J]. 激光与光电子学进展, 2015, 52(1): 011202.

Li Hui, Gan Lin, Zhang Wen-pan, et al. Simulation precision analysis of line of sight between bomb and target on hardware in the loop system for laser guided weapon countermeasure[J]. Laser & Optoelectronics Progress, 2015, 52(1): 011202.

[6] 廖洪波, 范世珣. 光电稳定平台伺服系统动力学建模与参数辨识[J]. 光学精密工程, 2015, 23(2): 477-485.

Liao Hong-bo, Fan Shi-xun. Modeling and parameter identification for electro-optical stabilized platform servosystems[J]. Optics and Precision Engineering, 2015, 23(2): 477-485.

[7] 周向阳, 刘炜. 航空遥感惯性稳定平台摩擦参数辨识[J]. 中国惯性技术学报, 2013, 21(6): 710-714. Zhou Xiang-yang, Liu Wei. Parameter identification of friction model on inertially stabilized platform for aerial remote sensing application[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 710-714.

[8] 黑沫, 张连超, 廖洪波. 机电联合建模在直驱伺服系统设计中的应用[J]. 光学精密工程, 2014, 22(9): 2416-2422. Hei Mo, Zhang Lian-chao, Liao Hong-bo. Application of mechatronic modeling to design of direct drive servo system[J]. Optics and Precision Engineering, 2014, 22(9): 2416-2422.

[9] Kouba G, Boely N. Fuzzy logic method use in F/A-18 aircraft model identification [J]. Journal of aircraft, 2010, 47(1): 10-17.

[10] Pattinson J, Lowenberg M H. Multi-degree-of-freedom wind tunnel maneuver rig for dynamic simulation and aerodynamic model identification[J]. Journal of aircraft, 2013, 50(2): 551-566.

[11] 黑沫, 范世珣, 廖洪波. 精密谐波传动系统建模[J].光学精密工程, 2014, 22(7): 1842-1849. Hei Mo, Fan Shi-xun, Liao Hong-bo. Modeling of precision harmonic drive system[J]. Optics and Precision Engineering, 2014, 22(7): 1842-1849.

[12] 朱炜, 芮筱亭. 压电执行器的Bouc-Wen模型在线参数辨识[J]. 光学精密工程, 2015, 23(1): 110-116. Zhu Wei, Rui Xiao-ting. Online parameter identification of Bouc-Wen model for piezoelectric actuators[J]. Optics and Precision Engineering, 2015, 23(1): 110-116.

Dynamic model identification and computation of servo system for simulation turntable

LI Hui, CHEN Qian-rong, ZHU Zhen, GAN Lin
(Luoyang Electronic Equipment Test Center of China, Luoyang 471003, China)

Simulation turntable is widely used in the simulation on electro-optical guided seeker and its countermeasure. Dynamic control precision and design efficiency of the servo system could be effectively improved by means of using parameter identification to obtain the high precision transfer function model of the simulation turntable for laser guided seeker. Based on this, a frequency response auto-testing method was proposed according to the servo system configuration of the simulation turntable, and the high precision transfer function model of the controlled object was obtained by adopting the parameter hierarchical identification. The comparison with actual data shows that the absolute magnitude error of the identification result was less than 1 dB, the absolute phase error was less than 2° in low frequency, and the mechanical syntony characteristic was also gained in high frequency of the servo system. Then the computation method on dynamic control precision for tracking servo system was analyzed, the closed-loop dynamic precision model was set up by frequency design modeling method combined with the adjustable control model and the high precision transfer function model of the controlled object. The simulation analysis, by contrasting actual tested dynamic control error data with simulation error data, shows that the dynamic control precision computation model can accurately show the variety rule of the dynamic error and dynamic process of the servo control system. The research results provide a model identification method to support and analyze the dynamic control precision modeling of the servo control system for the same type of devices.

simulation turntable; dynamic model; frequency response analysis; hierarchical identification; model identification

TP273; TP448

A

1005-6734(2015)03-0402-07

10.13695/j.cnki.12-1222/o3.2015.03.023

2015-02-18；

2015-05-28

总装重点资助项目（2013SY3310403）

李慧（1980—），男，博士，从事光电对抗仿真技术研究。E-mail：lihuiwch@163.com

��编号：1005-6734(2015)03-0409-06 doi: 10.13695/j.cnki.12-1222/o3.2015.03.024