基于罗德里格参数的线性最优估计自对准
梅春波,秦永元,杨鹏翔
基于罗德里格参数的线性最优估计自对准
梅春波1,秦永元1,杨鹏翔2
(1. 西北工业大学 自动化学院,西安 710129;2. 西安现代控制技术研究所,西安710111)
针对车载捷联惯导系统怠速条件下的初始对准问题,提出了一种基于罗德里格参数的线性最优估计自对准算法。利用姿态阵分解和凯莱变换,将任意姿态下的无初值初始对准问题简化为罗德里格参数的无约束线性最优估计问题。讨论了算法的有效性,推导了算法的对准误差公式,并设计了一种简洁的工程实现方案。利用车载捷联惯导系统进行了四位置对准试验,每个位置对准六次,结果表明,在发动机振动及外界随机扰动下,新算法可以在5 min内完成对准,统计方位均方差(1σ)不超过3′。
初始对准;罗德里格参数;凯莱变换;线性最优估计
传统的捷联惯导系统初始对准算法基本可分为两类:第一类,由粗对准和精对准构成,粗对准估计姿态初值,对惯导系统误差方程在姿态初值处进行线性化,精对准则采用线性卡尔曼滤波或线性最小二乘估计姿态初值误差,进而完成对准[1-2];第二类,以捷联惯导系统非线性误差模型为对象,采用非线性滤波[3-5]实现任意姿态角的初始对准。
上述两类算法中,第一类算法计算量小,所采用的技术手段已有成熟的工程应用;第二类算法则统一了对准过程,无需姿态初值,但计算量大。
本文以惯性系多矢量定姿为基础[6-9],通过引入罗德里格参数,将任意姿态下的无初值对准问题简化为一个无约束线性最优估计问题,从而得到一种新的对准算法。新算法在结构上与非线性滤波对准相同,无需姿态初值;在数值实现上则比分段对准算法更为简洁,兼具两种传统对准算法的优点。
1 惯性系多矢量定姿对准方案
惯性系基于矢量定姿对准方案以姿态阵链式分解为基础,

式中:n为导航坐标系,取为东北天地理坐标系;ni为导航惯性系,与对准开始时刻的n系重合;b为载体坐标系;bi为载体惯性系,与对准开始时刻的b重合。
根据上述坐标系定义,可得
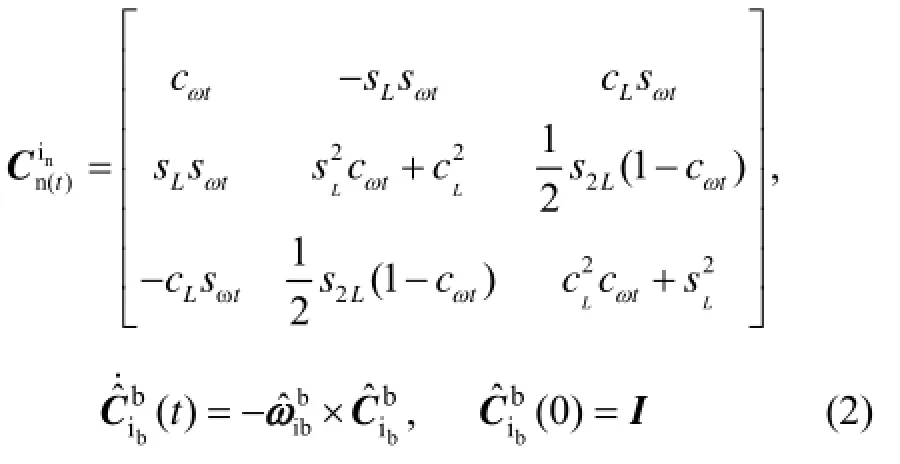
式中:cL=cos L,sL=sin L,cωt=cos(ωiet ),sωt=sin(ωiet ),s2L=sin(2L);ωie为地球自转角速率;L为对准点地理纬度信息;t为对准开始后持续时间;为陀螺仪测量角速度。
在车辆怠速、微幅晃动条件下,加计测量值可视为重力加速度在载体系内投影,即有
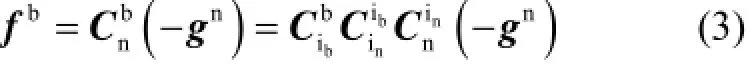
记
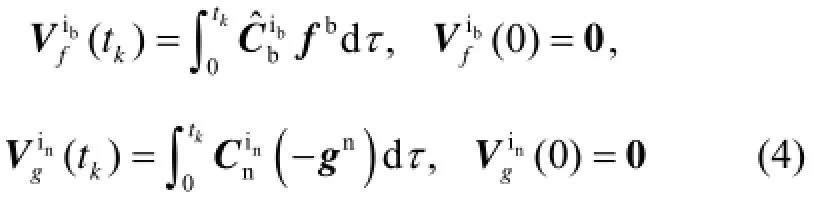
则有,在对准过程中任意时刻kt,
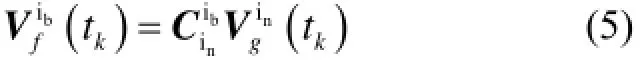
惯性系多矢量定姿对准算法的核心,即是利用式(5)所有时刻积分矢量的等式关系,给定代价函数,完成常值姿态阵的最优估计。然后,结合式(2)计算结果,利用式(1)关系得到对准过程中实时的姿态阵。
2 罗德里格参数最小二乘估计
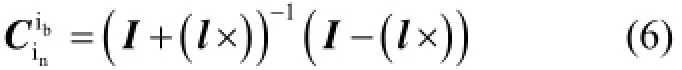
将式(6)代入式(5)中,有
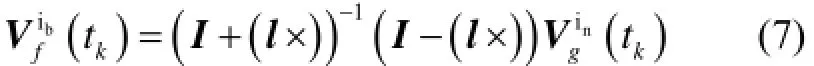
式(7)等号两端左乘(I+(l×)),移项整理得
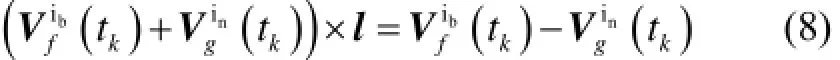
在上述推导中,并未对l有任何约束条件。依据(8)式,由全体离散积分结果设计代价函数:
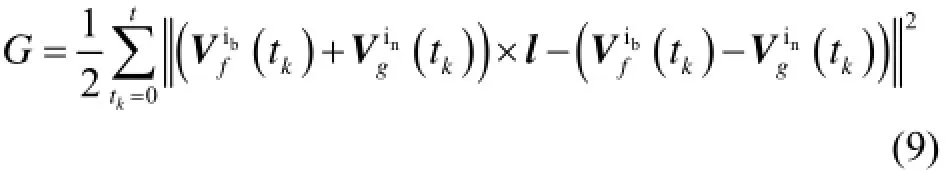
通过最小化G,即可得到l的一种最优估计。
进一步,考虑矢量用于定姿时,有效信息为其方向而非模值,故可对式(9)代价函数做等价变形,
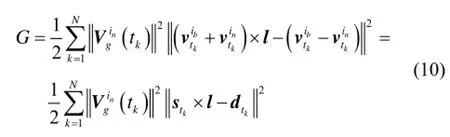
对式(10)两端同除以一个常数,不改变最优估计结果,故式(10)代价函数可等价描述为
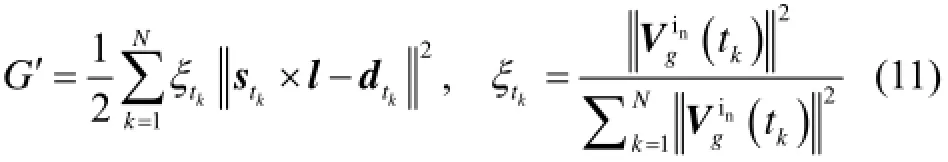
其中,ktξ可视为等效相对权重系数。
由式(11)可得l的加权最小二乘估计为
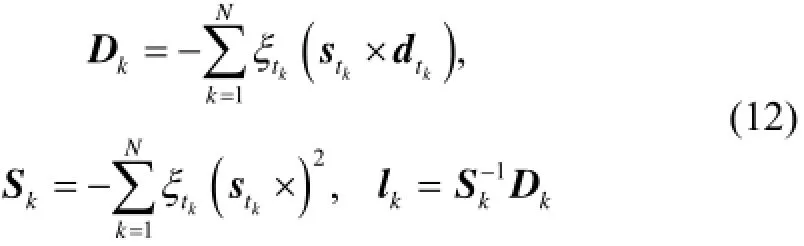
3 算法有效性及误差分析
3.1算法有效性分析
新算法通过求解式(2)和式(12)来完成对准,易知式(2)计算结果有效性与器件正常工作状态相关,而式(12)的有效求解则要求矩阵kS满秩。
由式(12)易知,当存在至少两个不同时刻的stk不共线时,Sk即为满秩。若in系至ib系等效旋转矢量为θ⋅r,θ为转角,r为转轴方向单位向量,则有
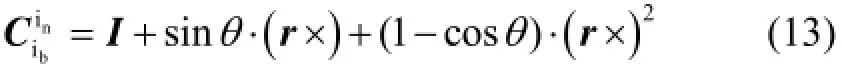
当θ=π时,有
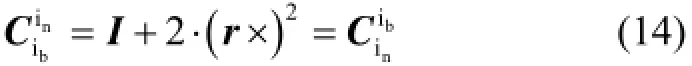
此时,将式(13)代入stk计算式,整理可得
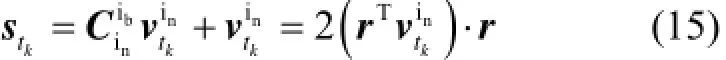
式(15)推导中,用到了恒等关系式I+(r×)2=rrT。
式(15)表明,当等效旋转矢量转角为π时,任意时刻的kts均与r共线,为算法的奇异点。
此时,直接采用式(4)(12)无法完成对准,在算法数值实现中将给出对该奇异点的处理方式。
3.2对准算法误差分析
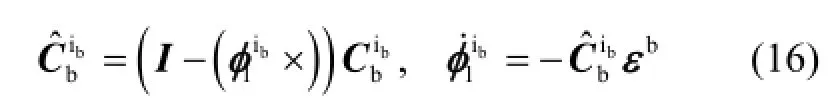
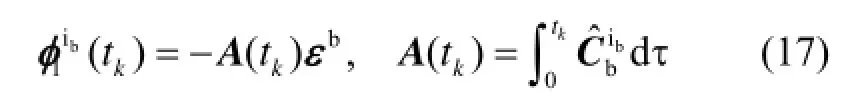
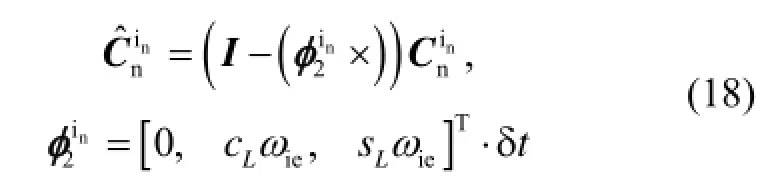
考虑陀螺漂移εb及加速度计零偏∇b影响,代入式(4),易得比力积分误差δ为
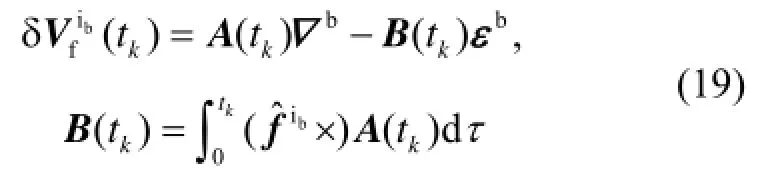
式中,A(tk)由式(17)给出。
为便于讨论且不失一般性,假定对准开始时刻导航系和载体系重合,由式(2)(4)(17)(19)经相应积分运算可得A(t )、B(t )、(t )近似时域解析表达式:k k k
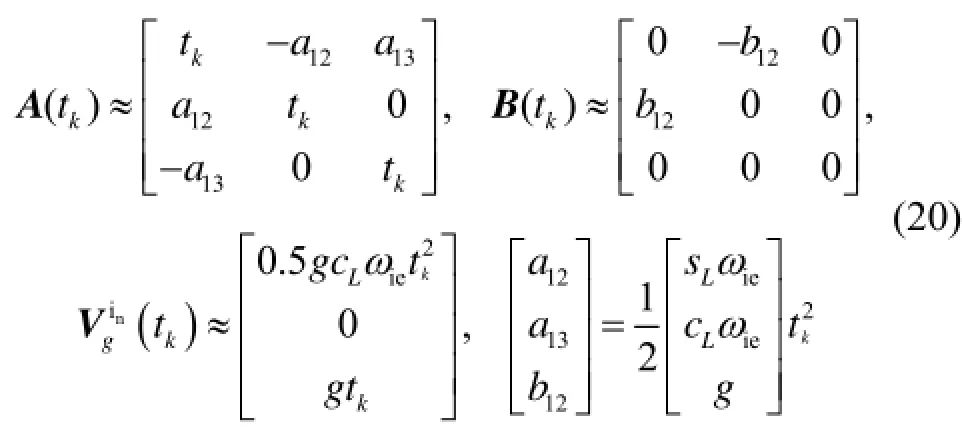
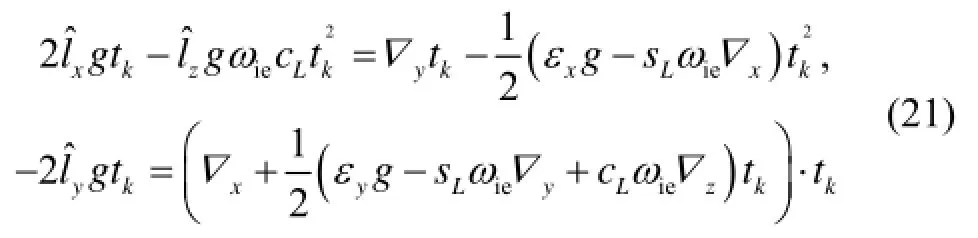
由式(21)可得ˆl的加权最小二乘估计解析值为
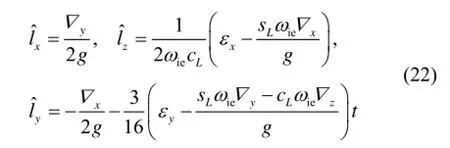
根据假定,ib系与in重合,罗德里格参数真值l为零。因此,式(21)得到的即是罗德里格参数估计误差δ,即δ=。此时,由式(6)可得估计姿态阵:
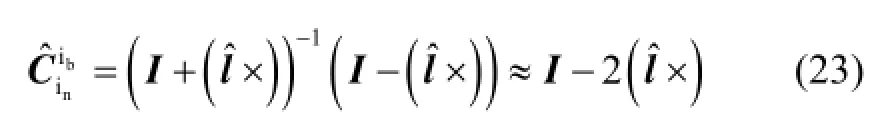
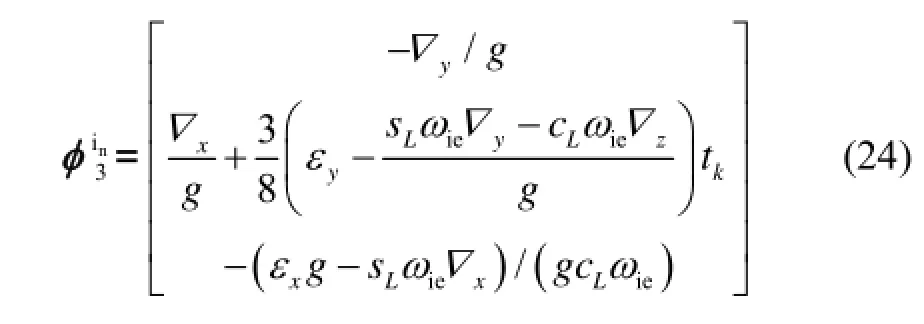
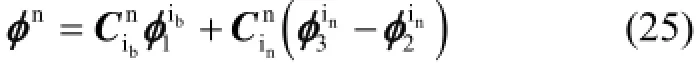
4 考虑奇异点影响的算法实现
由3.1小节分析结果知,当in系至ib系等效旋转矢量的转角θ为π时,行列式=0,此时不存在;当θ位于π的小邻域内时,为解决零值的小量,此时l的求解为严重病态问题。据此,可通过对Sk行列式设定阈值来判断算法是否位于奇异点附近。
若判断位于奇异点附近,可通过对ib系进行一个虚拟转动得ib1系,使in系至ib1系等效旋转矢量的转角远离π。然后,利用式(12)求解,又虚拟转动姿态阵准确已知,即可间接得到,完成对准。
进一步,对IMU系统近似为右前上安装的陆用车载导航系统而言,奇异点仅出现在水平姿态角为小角,方位角位于π附近时。此时虚拟转动可以唯一设定为:将bi绕着其z轴方向转动π角得到b1i,此转动姿态阵记为zC。
在上述讨论的基础上,经过适当地推导,可以得到消除奇异点影响的罗德里格参数递推整体最小二乘对准求解步骤为:
① 初始化其
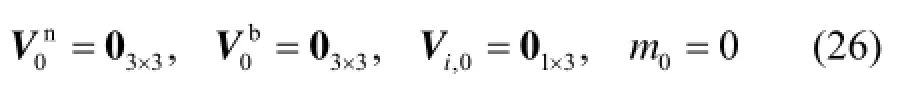
中,,,ixyz=。
② 递推更新
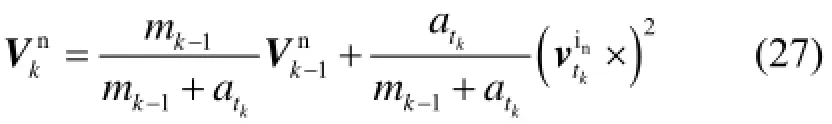
④ 对准实时姿态求解
5 试验验证
2013年12月在北京丰台区(纬度为40.067°),利用某型号车载光纤捷联惯导系统进行了四位置对准试验。每个位置,对系统断电重启,重复对准六次,对准时长设为5 min。对准过程中,车辆发动机处于怠速状态。对准算法中所用奇异点判别阈值设为1e-10。
由于对准是在室外导航车上进行,无姿态真值,为了评估算法的有效性,对同一组对准数据分别采用文中设计算法和传统的分段初始对准算法进行处理,从而间接验证所设计算法的有效性。分段对准算法中,采用惯性系粗对准和导航系卡尔曼滤波精对准,粗对准时长为60 s,精对准240 s。
考虑到对准的难点在于方位角估计,因此此处仅给出四位置上实时方位角估计曲线以及新算法与传统算法方位角最终估值。
图1~图4分别给出了不同方位下,六组重复对准试验实时方位角估计曲线。表1给出了对准结束时刻,新算法和分段对准算法各自得到的方位角估值及其统计结果。由图1~图4方位估计曲线及表1最终方位最终对准结果,可以得到如下结论:
第一,所设计算法无需姿态初值,即可实现任意方位角条件下的快速对准,且对准结果收敛速度与方位角的大小无关。
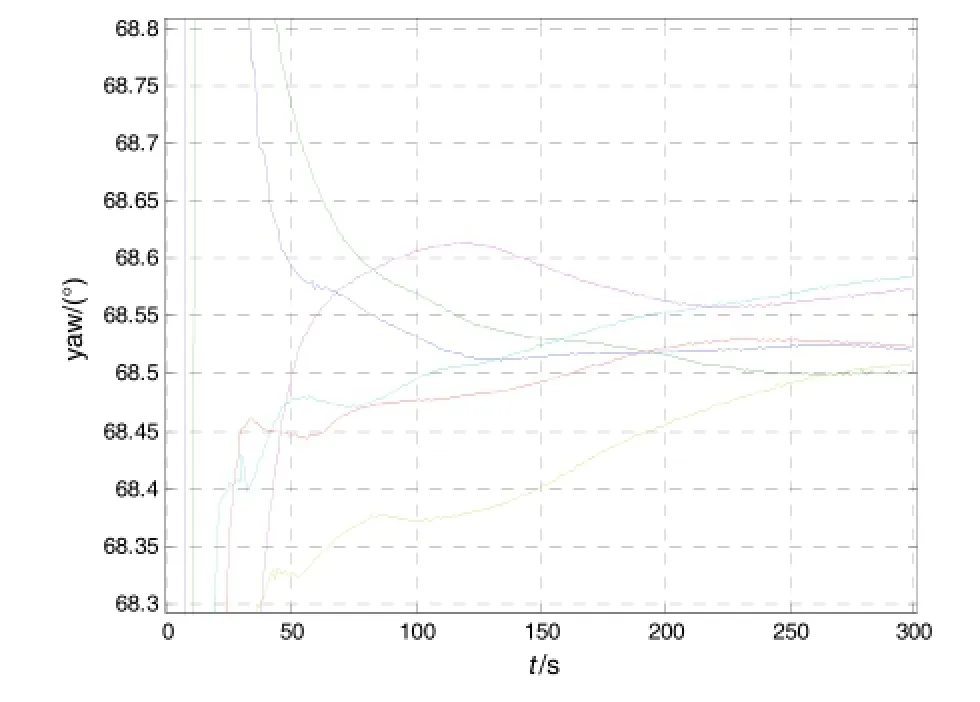
图1 方位1时航向角估计结果Fig.1 Estimation of yaw at Ori.1
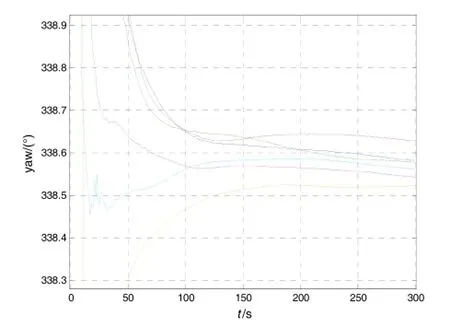
图2 方位2时航向角估计结果Fig.2 Estimation of yaw at Ori.2
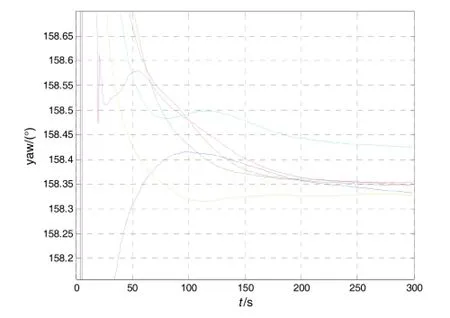
图3 方位3时航向角估计结果Fig.3 Estimation of yaw at Ori.3
第二,由于最小二乘算法的平滑作用,收敛曲线非常光滑,常规的卡尔曼滤波对准则难以做到这一点。
第三,对比表1中对准结束时刻两种算法方位角估值可知,新算法的对准精度与分段对准相当,而对准结果统计特性则略优于传统算法。
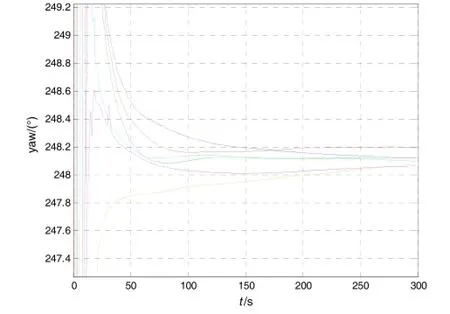
图4 方位4时航向角估计结果Fig.4 Estimation of yaw at Ori.4
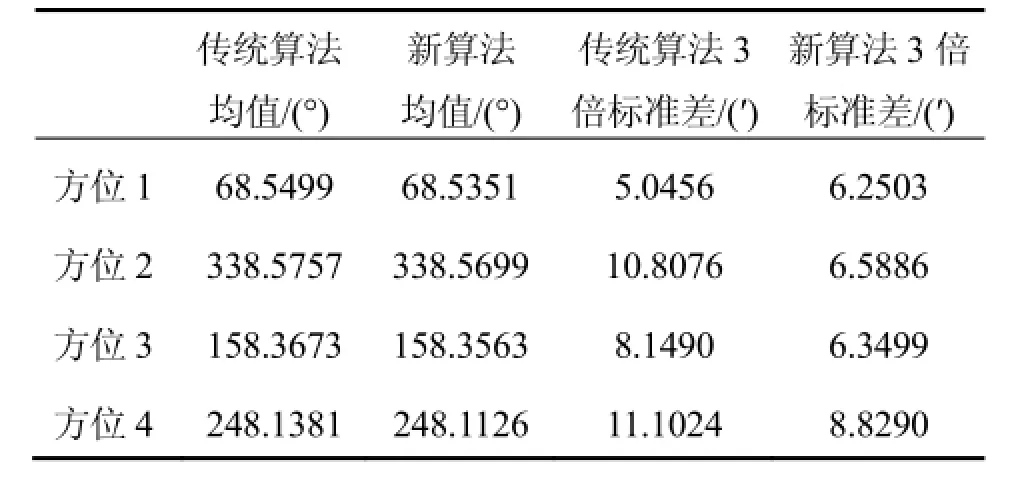
表1 对准结束时刻方位角对比Tab.1 Comparison of the final estimated yaw angles
6 结 论
针对车载捷联惯导系统怠速条件下的快速自对准,利用姿态阵分解和凯莱变换,推导得到一种以无约束最小二乘估计为核心的对准算法。该算法适应任意姿态初值且无需进行粗对准,计算简洁,便于工程实现。文中进一步采用试验数据对算法进行了充分的验证,表明了所设计算法无需任何初值及先验信息,而对于对准过程中的噪声和随机扰动却有更强的平滑能力,具有很好的工程应用价值。
(References):
[1] Dai H D, Zhou S L, Chen M, et al. Quaternion based nonlinear error model for rapid transfer alignment[J]. Journal of Astronautics, 2010, 31(10): 2328-2334.
[2] 钱华明, 葛磊, 彭宇, 等. 多渐消因子卡尔曼滤波及其在SINS初始对准中的应用[J]. 中国惯性技术学报, 2012, 20(3): 287-291.
Qian Hua-ming, Ge Lei, Peng Yu, et al. Multiple fading factors Kalman filter and its application in SINS initial alignment[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 287-291.
[3] 谢阳光, 伊国兴, 王常虹, 等. 高斯-厄米特滤波器在捷联惯导系统初始对准中的应用[J]. 航空学报, 2012, 33(3): 554-560.
Xie Yang-guang, Yi Guo-xing, Wang Chang-hong, et al. Application of Gauss-Hermite filter in SINS alignment[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 554-560.
[4] 丁国强, 徐洁, 周卫东, 等. EM-CDKF算法及其SINS初始对准应用[J]. 华中科技大学学报(自然科学版), 2014, 42(10): 31-36.
Ding Guo-qiang, Xu Jie, Zhou Wei-dong, et al. EM-CDKF algorithm and its applications on SINS initial alignment [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(10): 31-36.
[5] Wu M P, Wu Y X, Hu X P, et al. Optimization-based alignment for inertial navigation systems: theory and algorithm[J]. Aerospace Science and Technology, 2011, 15(1): 1-17.
[6] Wu Y X, Pan X F. Velocity/position integration formula partⅠ: Application to in-flight coarse alignment[J]. IEEE Transaction on Aerospace and Electronic Systems, 2013, 49(2): 1006-1023.
[7] 王跃钢, 杨家胜. 晃动基座下捷联惯导的抗干扰自对准算法[J]. 控制与决策, 2014, 29(3): 546-550.
Wang Yue-gang, Yang Jia-sheng. SINS anti-interference self-alignment algorithm for the swaying base[J]. Control and Decision, 2014, 29(3): 546-550.
[8] Peter M G S. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 1930-1941.
[9] Daniele M, Markley F L, Puneet S, et al. An optimal linear attitude estimator[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(6): 1619-1627.
Linear optimized self-alignment for SINS using Rodrigues parameters
MEI Chun-bo1, QIN Yong-yuan1, YANG Peng-xiang2
(1. School of Automation, Northwestern Polytechnical University, Xi’an 710129, China; 2. No.203 Research Institute of China Ordnance Industries, Xi’an 710111, China)
A method for fast initial alignment of SINS using Rodrigues parameters was proposed for land vehicles under complex disturbances. Through attitude matrix decomposition and Cayley transform, the alignment is transformed into an unconstraint linear optimization of Rodrigues parameters. The effectiveness of the algorithm was discussed, the error equations were deduced, and a simple implementation scheme was proposed. A four-position alignment experiments with 6 times each position was carried out by using the vehicle SINS under the engine vibration and external random disturbances. The results show that the new algorithm can converge within 5 min, and the root mean square (1σ) of yaw error is less than 3′.
alignment; Rodrigues parameters; Cayley transform; linear optimization
V249.3
A
1005-6734(2015)03-0298-05
10.13695/j.cnki.12-1222/o3.2015.03.004
2015-01-16;
2015-05-05
国家自然科学基金(61273333)
梅春波(1985—),男,博士研究生,研究方向为惯性导航、组合导航。E-mail:meichunbo@126.com
联 系 人:秦永元(1946—),男,教授,博士生导师。E-mail:qinyongyuan@nwpu.edu.cn

