例析数学复习课内化知识和技能的措施

韩香玲

常见的数学复习课长期以来都存在着许多问题，如果通过“追根溯源，内化知识结构”“探究简便算法，内化运用技能”“由浅入深，内化迁移性综合运用”就能让很枯燥的复习课蓬发出新的活力。

复习课知识技能内化“复习”一词在汉语词典中的意思是：“把学过的东西再学习，使巩固。”古代大教育家孔子曰：“温故而知新”，可见“复习”有巩固知识和为学习新知做铺垫的作用。然而也正是因为是“学过的东西”、是“温故”，因而数学复习课长期以来都存在着以下几个问题：

第一，练习题做得多，梳理知识结构少。忽视发散思维，知识迁移不够。教师往往重知识系统本身，很少引导学生思考与本系统有关的知识，让学生思维发散，实现知识迁移。

第二，追求知识层次目标多，着眼能力层次目标少。教师总有一种急功近利的思想，教学观念的陈旧。

第三，关注教材多，关注学生少。在备复习课时，大都表现为备教材，钻研教材是认真的，而备学生的意识不够，尤其是对学生的数学现实分析的不透彻。

针对以上问题我设计了一堂《有关角的复习课》进行尝试教学，效果较佳。

一、追根溯源，内化知识结构

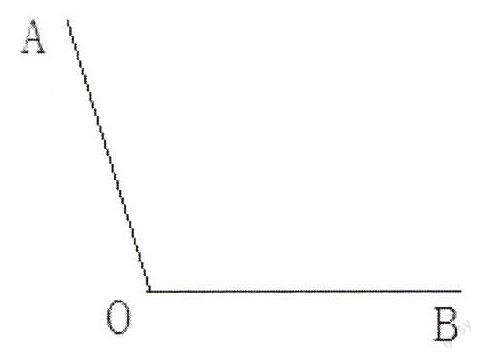
设计例题：例一、如图，∠AOB=98°40′30″，过点O作射线OC，使∠BOC=60°12′20″，求∠AOC的度数。

首先，投影仪打出题目，立即令学生进行解题操作，因为题目简单，很快学生就得出了解题过程和答案，但也有学生没有注意有多种可能性的存在，遗漏了射线OC在OB下方的一种情况，但这种错误被学生及时地纠正了。其结果如下：（1）当射线OC在OB上方时，∠AOC=∠AOB-∠BOC=98°40′30″-60°12′20″=30°28′10″。（2）当射线OC在OB下方时，∠AOC=∠AOB+∠BOC=98°40′30″+60°12′20″=158°52′50″。

接下来，我就提问：这个解题过程是怎么来的？依据是什么？（包括解题思路和运算过程），学生回答五花八门，有许多。我就进一步引导，什么是角？角怎样表示？角的大小如何比较？角的度量单位是什么？它们之间又如何转化？根据角的大小，角可以怎样分类？通过引导学生就恍然大悟，原来一道题目中包含这么多的知识！

因此，追根溯源找到解题的着眼点后，并回顾了角的一些基本知识，使知识点的回顾融入到题目中。再结合学生们的动手操作巩固了两角和差的计算及度分秒间的转化，也领会了当几何图形让我们自己作上去时，往往有多种可能性存在的解题思想。

二、探究简便算法，内化运用技能

引申：例二、在例一的基础上添加条件：若OM平分∠AOB，ON平分∠BOC，求∠MON的度数。

结合图一，大家尝试解题。经过学生们的尝试，呈现出不同的解答方案，有∠MON=∠AON—∠AOM、∠MON=∠CON—∠COM、∠MON=∠BOM—∠BON等，我看到这种情形就问，解这道题目的理论依据主要是什么？（目的：承接上题，巩固角平分线的定义）。学生回答，我补充并评价后，接着问，还有没有更加简便的方法？学生的激情一下子又调动起来，重新思考这道题目，纷纷提出新的方法，最后师生比较，得出较简便的一种计算方法：∠MON=∠BOM—∠BON= 12AOB— 12∠BOC。通过这样操作，在巩固角的和差计算的基础上，拓展了学生的解题思路，会去寻求多种解题渠道，探求其合理性和有效性，得到解题的捷径。

三、由浅入深，内化迁移性综合运用

变形1：上题图一中，∠AOB=60°，∠BOC=40°，其它条件不变，则∠AOC与∠MON的度数又是多少？

变形2：上题图一中，∠AOB=x，其它条件不变，则∠AOC与∠MON的度数又是多少？

变形3：上题图一中，∠BOC=y，其它条件不变，则∠AOC与∠MON的度数又是多少？

变形4：上题图一中，∠AOB=x，∠BOC=y，其它条件不变，则∠AOC与∠MON的度数又是多少？

从上面的结果中，你能找出∠AOB、∠BOC、∠AOC与∠MON间的关系吗？

拓展：线段的计算与角的计算存在着紧密联系，它们之间可以互相借鉴解法，请你模仿上些题设计一道以线段为背景的计算题，并写出其中的规律。

围绕角的计算為主线，展开变形，层层递进来探求角之间的关系，促使学生的思维也跟着递进。这里的问题设计具有一定的层次性，因为学生的学习水平和认知能力等方面的差距更加明显，即由易到难，循序渐进，一步一步引导学生将问题深化，揭示出解题规律，避免“吃不了”和“吃不饱”的现象发生。而拓展中设计一道以线段为背景的计算题，使得知识间进行贯通，学以致用，实现知识迁移，同时学生的思维得到开拓、发散，有“柳暗花明又一村”的感觉。在这里强调了问题的设计要注意引申，问题与知识的对应关系线要明显，有利于明确联系方向，有利于引导学生联想。总之，问题设计时要注意层次性、要注意引申、要注意问题对知识的覆盖要全面，要突出重点，要重视知识的发生发展过程和数学方法的探究过程，在这题中得到了很好的体现。

例一例二结束后，让学生尝试：若把图一改为图二，上述题又如何解答。学生经过刚才的学习后，来解答后一问就会有熟门熟路的感觉。因此对一个问题不能就题论题，而应进行适当引申和变化，逐步延续伸展，在培养学生思维变通性的同时，让学生思维变得更为深刻、流畅。

总之，数学复习课的目的就是提升学生平时所学的知识和技能，让这是知识和技能内化为自己东西，而不是去机械式地记住那些题目、知识、技能。

参考文献：

[1]义务教育数学课程标准.2011.

[2]七年级上册数学.浙江教育出版社，2012.

[3]徐士华.提高初中数学总复习课有效性的思考与建议.新课程学习（基础教育），2010，（10）.

[4]陈冬娟.初中数学复习课问题设计与思考.数理化学习，2011，（2）.