阈值策略下带扰动的广义Erlang(n)对偶风险模型*
周金乐,王传玉(安徽工程大学数理学院,安徽芜湖241000)
阈值策略下带扰动的广义Erlang(n)对偶风险模型*
周金乐,王传玉
(安徽工程大学数理学院,安徽芜湖241000)
摘要:在阈值分红策略下研究了带扰动的广义Erlang(n)对偶风险模型,在这个模型中得出了公司直到破产时刻为止的累积红利期望现值函数所满足的两个积分-微分方程,并求出了这种情况下的广义Lundberg基本方程,同时当模型中的利润额服从泊松分布的时候,得出方程的一般解。
关键词:广义Erlang(n)分布;对偶风险模型;阈值分红策略;积分-微分方程
破产理论中的红利问题最早是由DeFinetti[1]在纽约第15届精算师代表大会上提出来的。由此便产生了风险理论最前沿也最流行的分支:分红策略的研究。保险公司为了吸引更多的用户,将分红策略考虑进了很多保险业务中,即投保人可以得到传统保单规定的保险责任外,还可以从保险公司经营的利润中获得较高的投资回报。如文献[2]就是在Gamma-Omega模型中考虑了带障碍策略的分红问题,并获得当盈余为负值的时候,并求出此时的破产概率。文献[3]是对保险公司资产负债管理定量方法的一种多目标规划性的研究,同时考虑了分红的情形。
而现在由于经济全球化的加剧,国与国之间的竞争也越来越剧烈,其中自主创新在这种竞争中的作用也越来越明显。而经典风险模型中的的对偶模型最大的运用就是在产品研发过程对风险的监督(如制药以及其他产品研发),所以近几年以来,大量的文献中都对对偶模型进行了研究和说明。文献[4]推导出了在对偶模型下满足总贴现红利期望条件的一类积分微分方程,并以此得出在障碍策略下的红利表达式以及最初盈余和障碍值之间是独立的关系。文献[5]是在文献[4]的基础上将对偶模型从障碍策略情况下推广到阈值策略下,得出了相似的结论并且得出障碍策略就是阈值策略的极限情况。文献[6]在阈值分红策略下考虑带常利率的对偶风险模型,得出直到破产为止的总红利贴现值的期望值,文献[7]在带扩散扰动的对偶风险模型的研究门槛分红策略最后得出了总分红现值期望函数的更新方程。而文献[8]是对一个广义Erlang(n)对偶模型进行研究,得出了其破产概率和在阈值策略下其红利表达式。
基于以上情况,在文献[8]的基础上,将原来在阈值策略下对广义Erlang(n)对偶模型中研究红利的问题扩展到带扰动的广义Erlang(n)对偶模型。这样更加贴近现实中风险复杂化的现实。
1 模型介绍
考虑带有扰动的对偶风险模型,它的盈余过程可以表示为

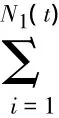
对盈余过程U(t)考虑一个阈值为b的阈值策略,当U(t)<b的时候,费用率为c1但不支付红利,当U(t)>b的时候,费用率变为c2,而且c2>c1即红利以c2-c1的比率来支付。则

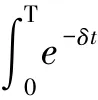
所以直到破产为止总的红利贴现值的期望为Vδ(u; b) = E[Dδ(b) |U(0) = u]。
记

2 积分—微分方程
2.1分红函数在0<u≤b时候U(t)满足的积分-微分方程
定理1当0<u≤b时,Vδ(u,b)满足下面的齐次积分—微分方程

证明设V1,j,δ(u; b)表示当0≤u≤b时并且处于状态j,V2,j,δ(u; b)表示当u>b时并且处于状态j的情形。则

考虑一个极小的时间dt,

由泰勒展开式知:

其中

把式(6)、(7)、(8)、(9)、(10)代入式(5),并且将两边同时除以dt,并令dt→0,当j=0,1,…,n-2。
则可以得到
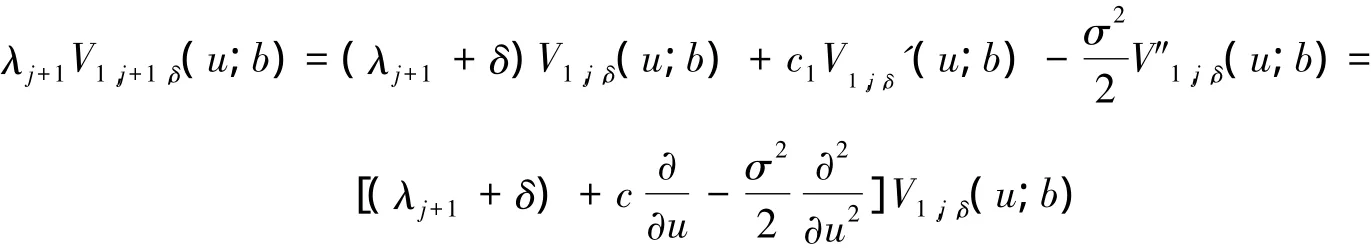
当j=n-1的时候

而V1,δ(u; b)是2m次可微的,则对于1≤m≤n-1。有

令m=n-1,对于式(11)来说V1,n-1,δ(u; b)是两次连续可微的。则V1,δ(u; b)是2n次连续可微的,故
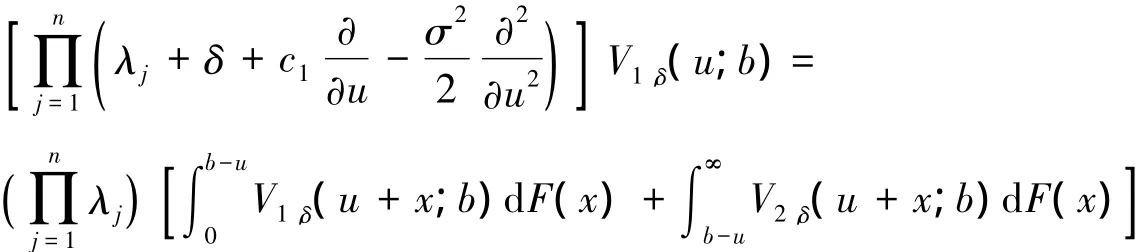
2.2分红函数在u>b时候U(t)满足的积分-微分方程
定理2当u>b时,Vδ(u,b)满足下面的齐次积分—微分方程
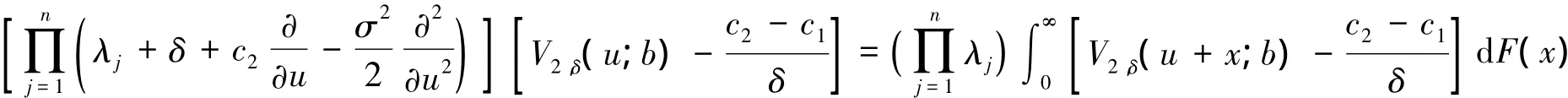
证明同理可以得到

可以转化为等式

接下来的证明同定理2.1类似,故省略。
3 广义Lundberg基本方程
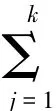
定义τ0=0并且U0=u则对于k=1,2,…
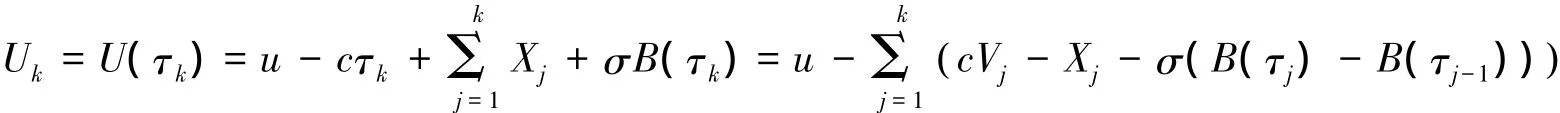
寻找一个s使得过程{e-δτk+sUk; k=0,1,2,…}表示一个鞅。这里的鞅条件等同于

即
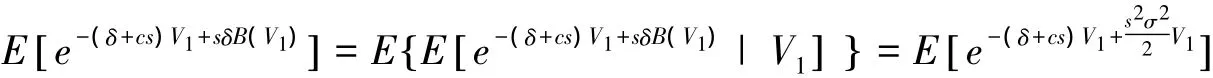
由于V1服从广义Erlang(n)分布,则式(12)可以表示为

所以该模型的广义Lundberg方程为

注,如果σ>0,则广义Lundberg方程式(13)在复平面的右侧有且只有n个根(具体证明可见文献[9])。
4 利润额服从指数分布时的直到破产为止总的红利贴现值的期望
在1所介绍的对偶风险模型下,假设利润额Xi服从参数为α的指数分布,即F(x) = 1-e-αx。当b<u<∞的时候,则将定理2.2的等式转化为
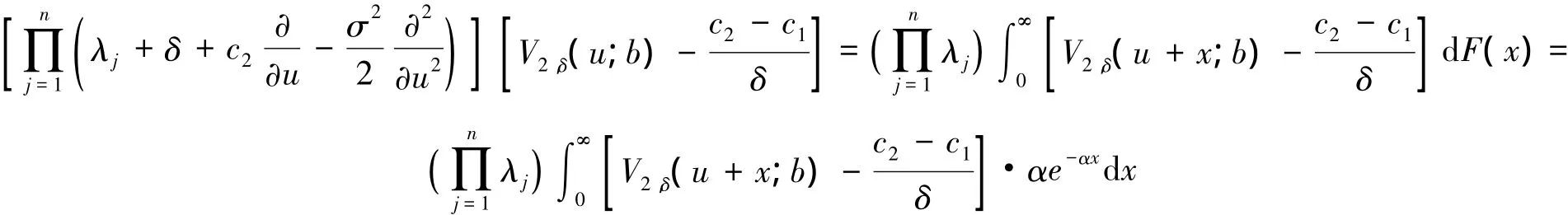

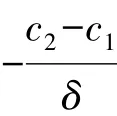
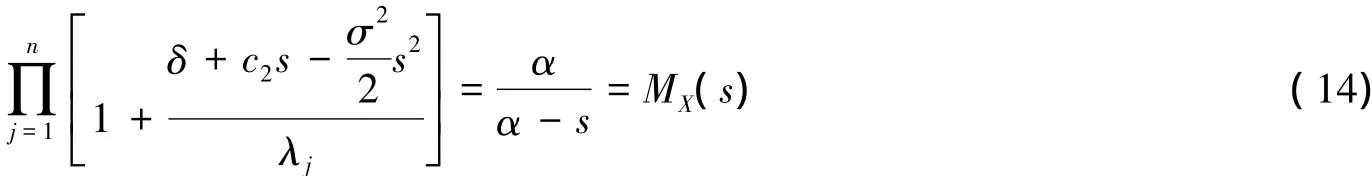
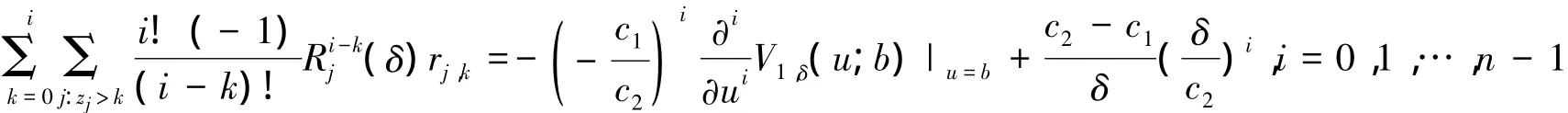
当0<b≤u的时候

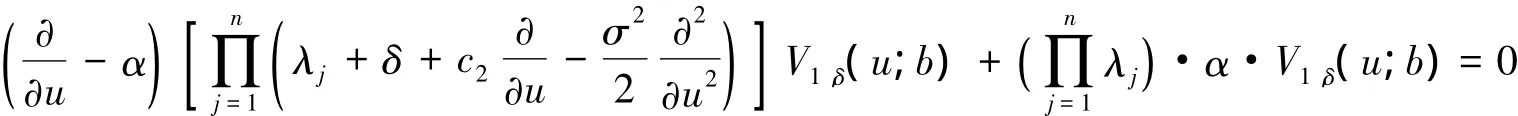
并且它的特征方程为

(与3所说的Lundberg基本方程一致)。所以可以得出

其中s0表示式(16)得唯一一个在复平面的左侧的根(唯一性有文献的说明类似,这里省略)。s1,…sl表示其他根的正实部并且重根数分别为m1,…,ml。而且等式中的q0,qj,k可以由下面的等式去确定(这些等式的具体证明与文献(8)类似,故这里省略)
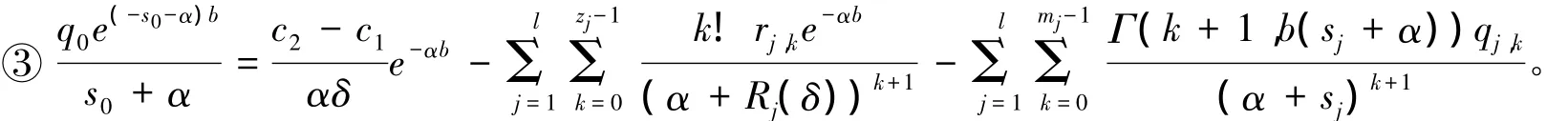
其中q0,qj,k,rj,k可以由上面的①,②,③来确定。而s0表示式(16)得唯一一个在复平面的左侧的根(唯一性有文献的说明类似,这里省略)。s1,…sl表示其他根的正实部并且重根数分别为m1,…,ml。同时R1(δ),…,Rm(δ)为方程(14)即3所说的该模型的Lundberg基本方程在复平面右侧的根而且他们的重数为z1,z2,…,zm。
5 结语
在阈值策略的条件下研究了带扰动的广义Erlang(n)对偶风险模型,得出了直到破产为止总的红利贴现值的期望值得表达式,使得对偶模型对新产品研发过程中风险的监督更加的贴近现实。同时为在对偶模型提供的保险实务中当利润产生次数并不完全遵循Poisson分布规律时候,即每个时间点上不止一次利润产生情形提供了解决方法。
参考文献:
[1]DE F T,Su un’Impostazione Alternativa Della Teoria Collettiva Del Rischio[J].Tran Sactions of the XVth International Congress of Actuaries,1957,2(1) : 433-443
[2]ALBRECHER H,GERBER H U,SHIU E S W.The Optimal Dividend Barrier in the Gamma-Omega Model[J].European Actuarial Journa,2011,1(1) : 43-55
[3]王爽.基于多目标规划的保险公司资产负债管理定量方法的研究[D].重庆:重庆工商大学,2012
[4]AVANZI B,GERBER H U,SHIU E S W.Optimal Dividends in the Dual Model[J].Mathematics and Economics,2007,41(1) : 111-123
[5]ANDREW C Y N.On a Dual Model with a Dividend Threshold[J].Insurance: Mathematics and Economics,2009,44(2) : 315-324
[6]何庆国,何传江.阈值分红策略下带常利率的对偶风险模型[J].经济数学,2012,29(4) : 67-70
[7]刘章,明瑞星,王文元,等.带扩散扰动的对偶风险模型的门槛分红策略[J].中国科学技术大学学报,2012,42(6) : 475-481
[8]CHEN Y,KRISTINA P S.The Ruin Time Under the Sparre-Andersen Dualmodel[J].Mathematics and Economics,2014,54(2) : 28-40
[9]SHUAN M L,JOSE G.The Gerber-Shiu Function in a Sparre Andersen Risk Process Perturbed by Diffusion[J].Scandinavian Actuarial Journal,2005,2005(3) : 161-186
A Generalized Erlang(n) Dual Risk Model of Threshold Policy With Perturbation
ZHOU Jin-le,WANG Chuan-yu
(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu 241000,China)
Abstract:A generalized Erlang(n) dual risk model with perturbation under a threshold dividend policy is researched.This paper derives a set of two integro-differential equations satisfied by the expected total discounted dividends until bankruptcy and finds the basic equations of generalized Lundberg in this case.When profit follows Poisson’s distribution,the solution to this equation is obtained.
Key words:generalized Erlang (n) distribution; a dual risk model; threshold dividend policy; integrodifferential equations
中图分类号:O152.4
文献标识码:A
文章编号:1672-058X(2015) 06-0001-06
doi:10.16055/j.issn.1672-058X.2015.0006.001
收稿日期:2014-10-12;修回日期: 2014-10-28.
*基金项目:国家自然科学基金(61203139) ;安徽省重点教研项目(2012jyxm277).
作者简介:周金乐(1989-),男,硕士研究生,安徽六安市人,从事精算学研究.

