犹豫模糊多属性决策的M-TOPSIS法*
李兰平(湖南财政经济学院基础课部,长沙410205)
犹豫模糊多属性决策的M-TOPSIS法*
李兰平
(湖南财政经济学院基础课部,长沙410205)
摘要:犹豫模糊集由于允许隶属度用几个数值的集合来描述,对于处理决策者对决策的信息表现出犹豫和优柔寡断情形特别适合,成为不确定多属性决策的又一有力工具;针对属性值为犹豫模糊元的多属性决策问题,提出了一种改进的TOPSIS决策法——M-TOPSIS决策法.并通过实际应用例子说明所提出的方法的有效性和实用性.
关键词:犹豫模糊集;多属性决策; M-TOPSIS
由于客观世界的复杂性和人类知识的局限性,在处理决策问题时,决策者往往很难用精确数来对各个评价方案的属性值给出描述.为弥补精确数的不足,Zadeh提出了模糊集理论,由于模糊数特别是区间数、三角模糊数等能较好地描述不确定信息.近年来模糊集以及直觉模糊集等已经被广泛应用到诸如人员选择、企业风险项目投资、供应商合作伙伴选择、企业厂址选择等多属性决策问题[1,2].最近,人们发现在很多决策问题中,由于决策者在做决策时常表现出犹豫和优柔寡断的状态,最终导致他们的意见不能达成一致,从而使得最终的决策结果也难以达成一致,而此种情形是前面的模糊数以及直觉模糊数难以较好描述的,为此Torra和Narukawa[3]提出了一种广义的模糊集——犹豫模糊集,其隶属度是由一列可能的数值组成的集合.针对犹豫模糊多属性问题,文献[4,5]利用算子进行信息集结的方法给出了多属性决策法;文献[6]针对属性值为犹豫模糊元的多属性决策问题,提出了VIKOR扩展决策法和TOPSIS决策法.犹豫模糊的概念刚被提出不久,针对犹豫模糊多属性决策问题的决策方法还不多见.由于传统的TOPSIS法存在着逆序问题以及综合评价值只反映了各评价方案内部的相对接近程度,而不能反映与理想的最优方案的真正接近程度[7-9].为此,针对属性值为犹豫模糊元的多属性决策问题提出一种改进的TOPSIS决策法,称为M-TOPSIS法.
1 犹豫模糊集的基本概念
定义1[3,4]设X是一给定集合.集合A = {<x,hA(x)>| x∈X}称为定义在X上的犹豫模糊集,这里hA(x)为定义在x∈X取值为[0,1]上的若干不同数值的集合,其表示元素x属于集合A的若干种可能的隶属度.为表述方便,文献[4]将hA(x)称为犹豫模糊元.
定义2[4]设h,h1和h2为3个犹豫模糊元,则其运算法则定义如下:
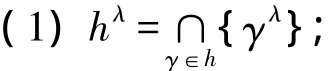

定义3[6]设h1和h2为定义在X = { x1,x2,…,xn}上的两个犹豫模糊元,则h1和h2之间的规范化Hamming距离定义为

其中l(h)为模糊结构元h中元素的个数.由于多数情况有l(h1)≠l(h2),故此处定义l=max{ l(h1),l(h2) }.并且为保证运算进行,需要将元素个数少的模糊结构元h进行扩充.具体的办法是将h中某元素重复添加.采用文献[6]的做法,如果决策者为风险偏好的,重复添加最大值,如果决策者为风险厌恶的重复添加最小值.例如h1={ 0.2,0.3,0.4},h2={ 0.4,0.6},则显然l(h1)>l(h2).则为保证运算进行,需要将h2的元素扩充到与h1的元素个数相同.于是当决策者为风险偏好的,令h2={ 0.4,0.6,0.6} ;当决策者为风险厌恶的,令h2= { 0.4,0.4,0.6}.
在接下来的讨论中,均设决策者为风险厌恶的.
2 犹豫模糊多属性决策的M-TOPSIS法
TOPSIS法是一种应用十分广泛的静态综合评价方法.在实际应用中,TOPSIS法存在着逆序问题.而且其综合评价值Ci只能反映各评价对象内部的相对接近度,并不能反映与理想的最优方案的接近程度;评价值Ci区分各评价对象优劣的范围也有局限.鉴于TOPSIS法应用的广泛性,有必要对TOPSIS法的不足进行改进.文献[8]提出一种新的改进的TOPSIS法,称为M-TOPSIS方法,不仅具有强保序性,而且比传统TOPSIS法灵敏.根据文献[8]的思想,针对属性值为犹豫模糊元的多属性决策问题,提出了基于M-TOPSIS法的决策方法,具体计算步骤如下:
步骤1基于犹豫模糊元的多属性决策矩阵建立.
对于某一多属性决策问题,设A1,A2,…,Am是m个待评价的备选方案,O={ o1,o2,…,on}是属性集.专家们给出了方案Ai在属性oj下的属性值hij(这里hij为犹豫模糊元),并设相应的属性权重向量为w =(w1,w2,…,wn),从而构成决策矩阵:

步骤2定义正、负理想解[6].
步骤3分别计算方案Ai到正理想解A*和负理想解A-的距离.
方案Ai到正理想解A*的加权距离定义为

方案Ai到负理想解A-的加权距离定义为

步骤4建立D+oD-坐标平面,以oD+作为x轴,以oD-作为y轴.备选方案点Ai用此坐标面上的点(,)来表示.令对应的方案为最优参考方案A.则备选方案Ai与最优参考方案A的欧氏距离为


取c(Ai,A)值较小的评价对象为较优,即在评价方案与最优参照点A等距离的情况下,则选择与次优参照点B相对距离较近的点为较优.
3 应用实例
为说明所提出的方法的有效性和可行性,采用文献[6]的例子进行说明.设某公司的董事会想在未来5年内投资某大型项目,经过初期调研和讨论确定了4个备选的投资项目A1,A2,A3,A4,有4个评价指标(属性),分别为金融前景o1;顾客满意度o2,商业国际化角度o3;学习和成长力o4.这4种属性的权重向量w = (0.2,0.3,0.15,0.35).为避免董事会成员的相互影响,成员以匿名的形式给出他们的属性偏好,最终得到表1所示的犹豫模糊决策信息.

表1 犹豫模糊决策矩阵
下面利用所提出的M-TOPSIS法对备选方案进行排序和择优.
步骤1确定正、负理想解.
步骤2计算备选方案Ai与最优参考方案A的欧氏距离分别为
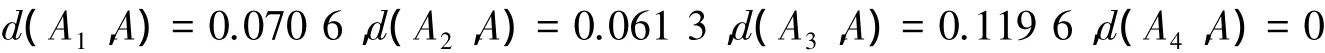
步骤3按照d(Ai,A)从小到大的顺序,得到最优的投资项目为A4,且总的优劣排序为A4>A2>A1>A3.这也恰与文献[6]中采用TOPSIS方法得到的.
4 结论
针对目前经常出现的多个决策者在进行重大决策时意见不统一,经常表现出犹豫和优柔寡断状态.犹豫模糊集理论在此背景下被提出,但是针对属性值为犹豫模糊元的多属性决策问题的研究还不多见,提出了一种新的多属性决策方法——M-TOPSIS法.并通过应用实例说明了所提出的方法的可行性和有效性.决策方法运算简单,便于利用Matlab等语言进行模块化操作.
参考文献:
[1]卫贵武.基于投影的直觉模糊数多属性决策方法[J].管理学报,2009(9) : 1154-1156
[2]刘希梅,孙少华,么慧慧,等.基于三角模糊层次分析法的教学质量评价研究[J].重庆工商大学学报:自然科学版,2013,30 (8) : 45-49
[3]TORRA V,NAEUKAWA Y.On Hesitant Fuzzy Sets and Decision,in: The 18th IEEE International Conference on Fuzzy Systems [J].Island Korea,2009,21: 1378-1382.
[4]XU Z S,XIA M M.Hesitant Fuzzy Information Aggregation in Decision Making[J].International Journal of Approximate Reasoning,2011,52(3) : 395-407
[5]WEI G W.Hesitant Fuzzy Prioritized Operators and Their Application to Multiple Attribute Decision Making[J].Knowledge-Based Systems,2012,31: 176-182
[6]ZHANG N,WEI GW.Extension of Vikor Method for Decision Making Problem Based on Hesitant Fuzzy Set[J].Applied Mathematical Modeling,2013,37(7) : 4938-4947
[7]俞立平,潘云涛,武夷山.修正TOPSIS及其在科技评价中的应用研究[J].情报杂志,2012,31(6) : 103-107
[8]王一任,任力锋,陈丽文,等.一种新的改良TOPSIS法及其医学应用[J].中南大学学报:医学版,2013,38(2) : 196-201
[9]赵萌,邱菀华,刘北上.基于相对熵的多属性决策排序方法[J].控制与决策,2010,25(7) : 1098-1100
Hesitant Fuzzy Multi-Attribute Decision-making Based on M-TOPSIS Method
LI Lan-ping
(Department of Basic Subjects,Hunan University of Finance and Economics,Changsha 410205,China)
Abstract:Because membership degree can be described by a set of several numerical values,hesitant fuzzy set is very suitable to deal with the decision problem with decision makers having hesitant attitude,and it becomes another powerful tool for multiple attribute decision making.For the attribute value is multiple attribute decisionmaking problem of hesitant fuzzy elements,an improved TOPSIS decision method is proposed,named M-TOPSIS method.Finally a practical example is given to illustrate the validity and practicability of the proposed method.
Key words:hesitant fuzzy set; multi-attribute decision-making; M-TOPSIS
中图分类号:151.2
文献标识码:A
文章编号:1672-058X(2015) 06-0007-04
doi:10.16055/j.issn.1672-058X.2015.0006.002
收稿日期:2014-10-08;修回日期: 2014-11-03.
*基金项目:湖南省科技厅科技项目(2013FJ3083).
作者简介:李兰平(1981-),女,湖南永州人,副教授,硕士,从事模糊多属性决策研究.

