居民消费对短期经济增长的实证研究

罗国旺，浦　号(遵义师范学院数学与计算科学学院，贵州遵义563002)



居民消费对短期经济增长的实证研究

罗国旺，浦号
(遵义师范学院数学与计算科学学院，贵州遵义563002)

摘要:在生产函数的理论基础上，研究居民消费变量对短期经济增长的贡献率;以西部1999-2008年的面板数据为依据，建立了以时间为影响的时点固定效应模型，研究了我国西部居民消费对经济增长的促进状况;研究结果表明:居民消费对经济增长是规模报酬递增的，并且居民消费对经济增长的贡献率呈现出逐渐增强的趋势。

关键词:居民消费支出;单位根检验;协整性

从生产函数的拓展模型出发，研究居民消费与经济增长的关系。曹丰［1］等人在C－D生产函数的基础上引入电力消耗这个变量，然后用面板数据对模型的参数进行估计，得出的结论是电力消耗对经济增长的贡献率很大;金福良［2］等人在C－D生产函数的基础上引入农村基础实施这个变量，采用时间序列数据研究湖北省农村基础设施对经济增长的影响，结论是湖北省农村基础设施对湖北省的经济增长具有规模报酬递增的作用。以上是基于C－D生产函数的经济增长研究，模型也大同小异，但所研究的经济增长的因素都是单一的。现以我国西部1999－2008年的面板数据为依据，在C－D生产函数的基础上引入消费这个变量，主要把模型分为规模报酬不变和规模报酬不变两大类。研究结论发现，西部各地区消费对经济增长的贡献度有很大的提升空间，对经济的增长都是规模报酬递增的作用，同时西部各地区的投资对经济增长也都是存在规模报酬递增的作用。

1　基于C－D生产函数理论的拓展模型

在20世纪30年代，由阿默斯特学院数学家柯布和美国芝加哥大学的经济学教授道格拉斯共同提出的C－D生产函数［3］，简称C－D生产函数，简单而科学地揭示了经济学中的生产本质，自产生以来一直被经济学家们广泛使用。实证研究主要在C－D生产函数的框架内展开的，利用C－D生产函数估计产出弹性。传统的柯布－道格拉斯生产函数为

式(1)中，Y表示产出; A是常数项，即衡量知识与技术进步、产业结构与制度等因素的全要素生产率; K为资本投入; L为劳动投入;α、β分别为资本投入和劳动投入的产出弹性。在柯布-道格拉斯生产函数的基础上将居民消费H引入到生产函数式(1)中，且对函数的每个变量做适当的调整，即得到式(2)所示的函数:

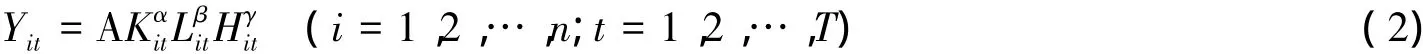
其中，以式(2)中的Yit、Kit、Lit、Hit分别表示第i地区在时间点t时刻的产出、资本投入、劳动投入以及居民消费(货币形式表示)，很显然α、β、γ就分别为Kit、Lit、Hit的产出弹性系数，若α+β+γ=1，则模型是规模报酬不变，否则，α+β+γ＜1说明模型是规模报酬递减;α+β+γ＞1说明模型是规模报酬递增。对式(2)左右两边分别取对数得到:

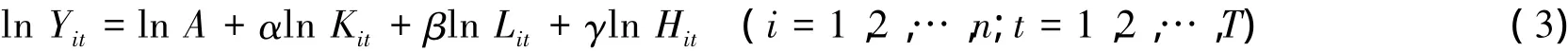
模型1:假设模型是规模报酬不变:则α+β+γ=1，这时β=1－α－γ带入式(3)可以化为

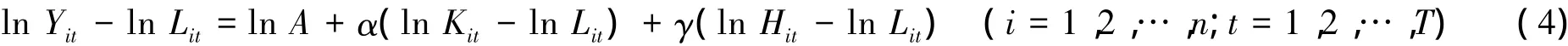
模型2:假定模型是规模报酬可变:为了更方便地研究居民消费对经济增长的作用，设定α+β= 1，即Kit资本投入和劳动投入Lit对经济增长是规模报酬不变，而居民消费Hit对模型的规模报酬具有可变性的特性。若γ＞0时，居民消费对经济增长存在规模报酬递增，若γ＜0时，反之，存在规模报酬递减。把β=1－α带入式(3)得到:

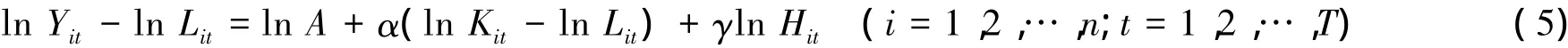
在实际数据的基础上分别对式(4)、(5)两种情况进行回归，对于模型的规模报酬递增和递减，可以通过回归所得的统计量和各个系数进一步分析可得知。同时，通过回归所得结果可以进一步分析居民消费对经济增长的拉动情况［4］。

2　我国西部地区经济增长研究

通过基于C－D生产函数理论的理论模型理论下，以西部10个省(直辖市)的经济增长为例，研究西部各地区1999－2008年的居民消费对经济增长的贡献状况。

2.1各变量的选择以及数据的获取

选取的产出变量Yit用各地区的GDP来表示，但统计年鉴里给出的GDP都只是当年价格的GDP即:名义的GDP，而不是实际GDP，所以统一按平减指数的方法折算成1997年不变价;由于统计年鉴里没有提供资本存量数据，故在这里主要是用资本形成总额来表示投入变量Kit，资本形成总额在统计年鉴中即包涵了固定资本形成与库存增加，通过利用固定资产投资价格指数，将所有资本形成总额按照以价格平减指数折算成1999年为基年不变价处理;投入变量Lit是采用各地区的就业人员(这里的就业人员是各省/直辖市在各自的《统计年鉴》中公布的第一产业就业人员、第二产业就业人员和第三产业人加总的数据) ;居民消费Hit是利用《中国统计年鉴》里的城镇居民家庭平均每人全年消费性支出表示，同理把所有的居民消费支出都按价格平减指数折算成1999年不变价。所选的变量数据主要是来源于《2000－2009年中国统计年鉴》与《新中国60年统计资料汇编》中。

2.2数据的单位根检验和协整性检验

因为研究的重点是西部各个省/直辖市的居民消费和经济增长的回归关系，所以涉及到面板数据的单位根检验(即平稳性检验)和协整检验，以避免产生伪回归现象。

面板数据的单位根检验:单位根检验［5］:对面板数据zit生成AR(1)过程，根据对Δzit－1的系数ρi的不同限制，面板数据单位根的两大类检验方法:相同根情和不同根情形下的检验。

相同根下的单位根检验(LLC检验)

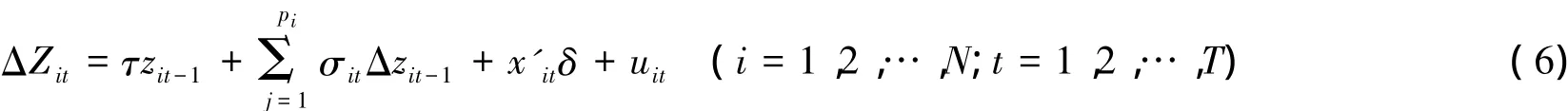
其中，τ=ρ－1; pi为第i个截面成员的滞后期数，原假设是面板数据中的截面序列具有一个单位根。具体步骤:给定截面成员的滞后阶数后，从Δzit和Δzit－1中剔除Δzit－1和外生变量的影响，并进行标准化求出代理变量;用代理变量做回归:Δ槇z=τz槇it－1+εit估计参数τ，进而根据构造统计量的临界值作出判断。

不同根下的单位根检验:可以根据Fisher-ADF综合各个截面检验结果的基础上，构造出统计量，对整个面板数据是否含有单位根作出判断。

以所建立的模型1和模型2分别对他们的回归变量进行面板数据的单位根检验，通过借用Eivews 6.0软件可得到如表1所示结果。

表1　面板数据的单位根检验

从表1知: ln Hit、ln Yit－ln Lit、ln Kit－lnit、ln Hit－ln Lit的4种检验统计量均在1%的显著性水平上不显著，故不能拒绝存在单位根的原假设，所以ln Hit、ln Yit－ln Lit、ln Kit－ln Lit、ln Hit－ln Lit都存在单位根，都是非平稳的;而Δ(ln Hit)、Δ(ln Yit－ln Lit)、Δ(ln Kit－ln Lit)、以及Δ(ln Hit－ln Lit)的4种检验统计量均在1%的显著性水平上显著，故拒绝存在单位根的原假设，即都不存在单位根，故均为一阶单整。

面板数据的协整性检验:以上所进行的单位根检验已经通过，即都是一阶单整的，下一步还必须对序列进行协整性检验，即:以1999年Pedroni提出的面板数据的协整性，否则就可能出现“伪回归”的现象［6］。

针对模型1及模型2的2种模型变量间的协整性，通过借助Eivews 6.0软件［5］进行协整性检验，得到结果(表2、3) :

表2　针对模型1的回归变量进行协整性检验

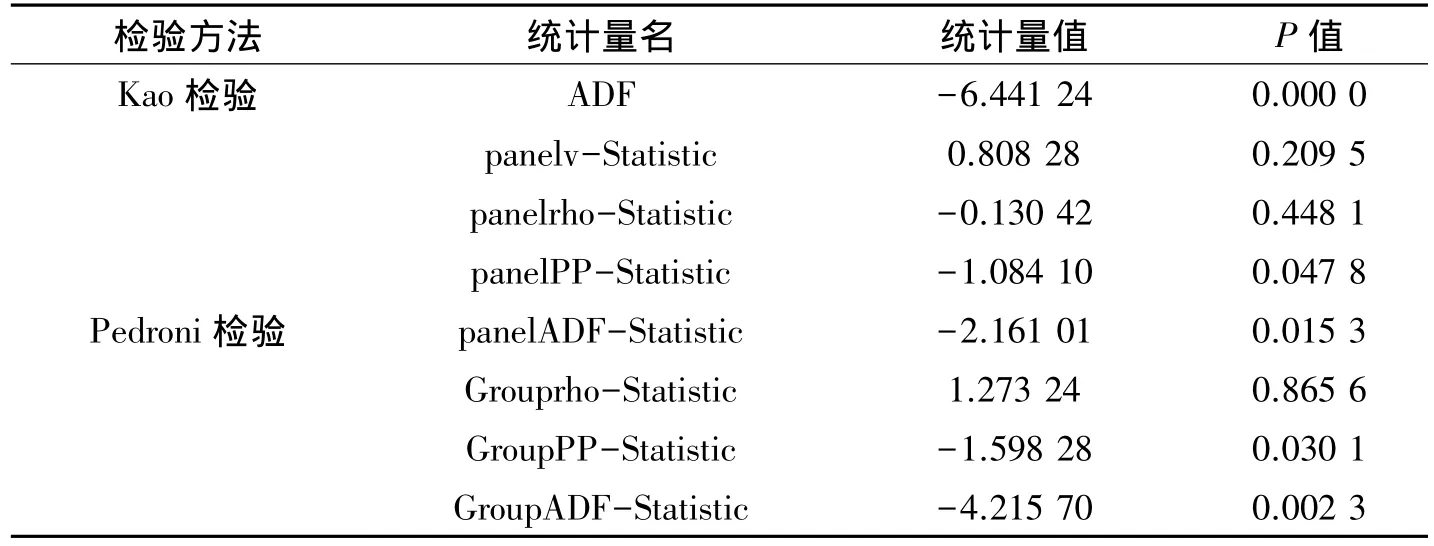
表3　针对模型2的回归变量进行协整性检验

通过对模型1和模型2的变量分别进行协整性检验发现，模型1和模型2都有5项检验统计量在1%的显著水平下支持存在协整关系，即认为模型1和模型2的变量间都分别存在协整关系，故可以对模型1和模型2变量进行回归。

2.3对模型的系数进行回归估计

因为研究的是样本本身，故应建立固定效应模型，当然了，可以通过借用Eivews 6.0软件先对模型1和模型2进行Hausman检验，结果发现:模型1的随机效应模型Hausman Test统计量为91.443 57和，P值是0.000 0＜0.05;模型2的Hausman Test统计量为13.876 66，P值是0.000 0＜0.05。故以上两种模型都拒绝原假设:随机影响模型中个体影响与解释变量不相关。所以认为个体效应与回归变量相关，所以应该建立固定效应模型。

为了研究西部不同地区居民消费对经济增长的贡献状况，同时，又因为不同时期西部地区平均生产要素的的利用率不一样。为此建立了以时间为影响的时点固定效应模型(系数可变) :通过借助Eivews 6.0软件对式(4)、(5)进行估计得结果:

模型1的估计:

备注:括号里的值是t统计量所对应的P值。

模型2估计:

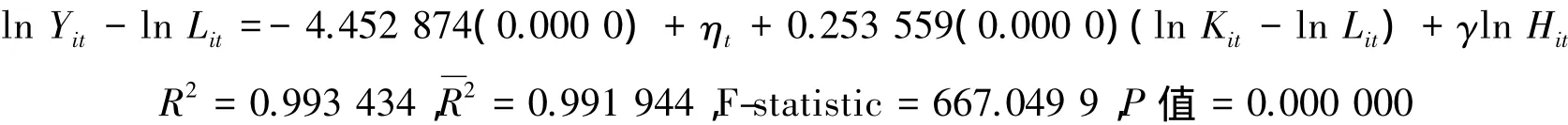
备注:方程下方的括号里是t统计量所对应的P值

从模型1和模型2所估计出来的结果中可以发现，模型2的R2值和2值以及F-statistic都要比模型1 的R2值和2值以及F-statistic都要大，故模型2比模型1要拟合得好，即认为模型是规模报酬可变的。

因为通过研究发现模型是规模报酬可变的，所以后面的研究都是针对模型2而进行的，对模型2深入研究得到:方程中反映不同时期西部地区平均生产要素利用水平ηt估计值，和反映西部不同地区居民消费对经济增长的贡献状况γi如表4所示。

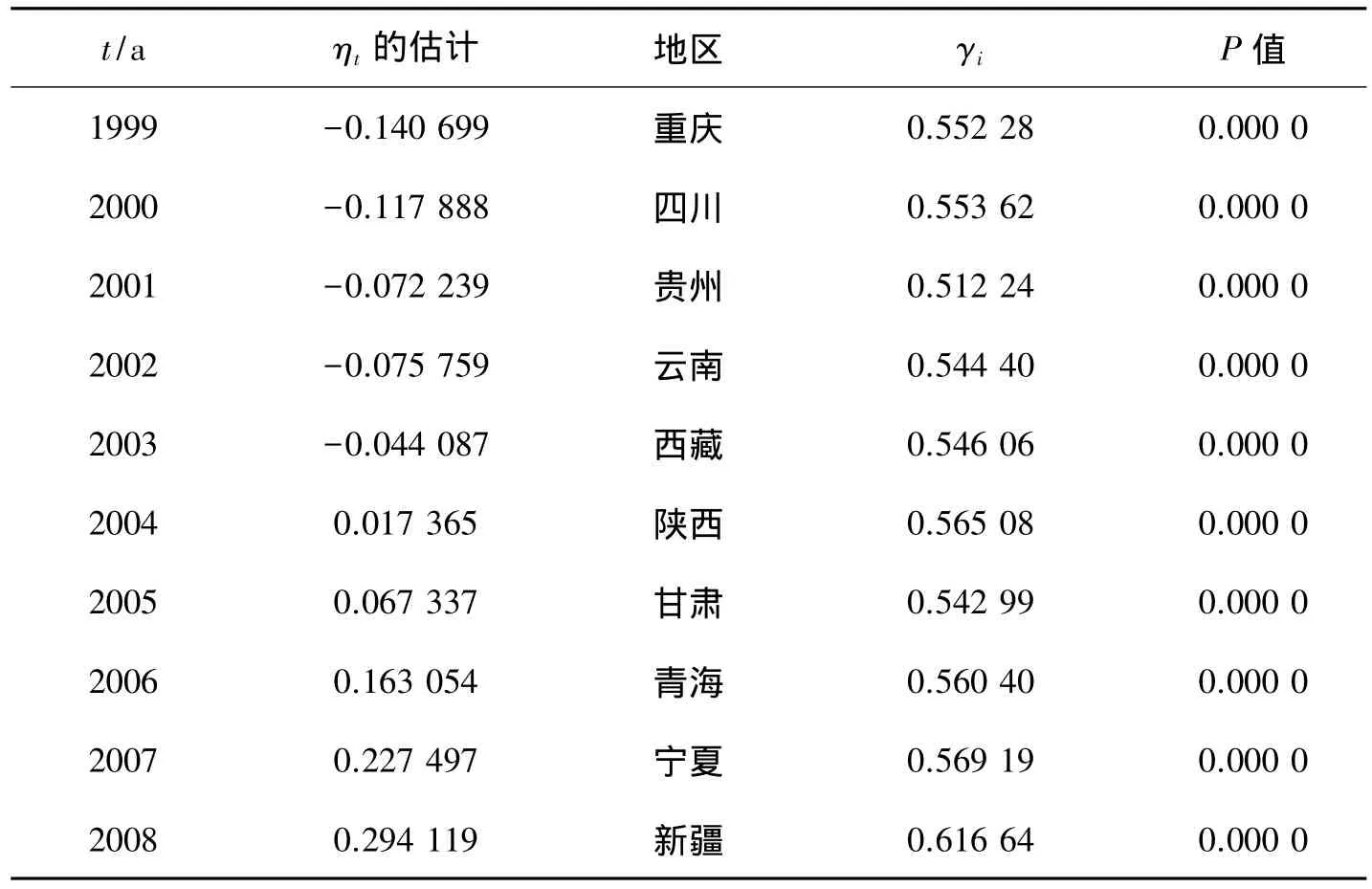
表4　不同时期的平均生产要素水平和地区消费产出弹性

以式(5)所估计出来的结果表明方程拟合得很好，所有T统计量在1%的显著性水平下都通过显著性检验。首先，如表4所示，式(5)所估计出来的生产要素利用率有正值和负值，说明不同时期西部区平均生产要素利用水平ηt有明显差异。并可以发现西部地区平均生产要素利用水平随时时期增加而逐渐增长的过程，在2003年以前平均生产要素利用率为负值，说明这段期间西部地区平均生产要素利用率底下，2003年后西部地区平均生产要素利用率为正值且成逐渐递增的状态，说明西部地区平均生产要素利用率不断提高的过程，这和曹丰，黄淑芬，许健榕［2］等研究的结果基本一致。再次，从表4所示的结果中可以看出，γi都是大于0的，则说明西部各地区的居民消费对经济增长都是规模报酬递增的。并且可以发现西部不同地区居民消费对经济增长的贡献率有所差异，其中，新疆居民消费对经济增长的贡献度最高，贵州最低，这和实际是基本吻合的，因为新疆是个旅游的圣地，拥有美丽的自然风光和各种特色饮食以及各种精美的修饰品，这促进了居民消费的增加，从而也带动了当地的经济发展，而贵州是西部比较落后的地区，虽然拥有丰富的自然资源，但欠开发，没有被充分利用，而且地理环境不占优势等各种原因导致了居民消费低，自然影响了地区的经济发展。

3　结语

研究是在基于C－D生产函数的基础上，引入消费变量，和以往研究者最大不同的地方是以往的研究者们都只是单独研究新引入变量对经济增长的贡献状况，现在同时考虑了消费变量在物质资本和劳动力资本投资变量的共同影响作用下，通过对模型可能存在的形式进行讨论假设，分别研究消费和资本对经济增长贡献状况。在规模报酬可变的前提下，通过Hausman检验对随机效应模型和固定效应模型进行选择，通过检验得知所建立的模型更符合固定效应模型，又对固定效应模型进行了分类讨论，即分以时间为影响的时点固定效应模型(系数可变)和以不同地区为影响的个体固定效应模型(系数可变)，通过这两个模型分别研究消费对经济增长的影响的状况。当然了，现在物质资本变量选取中是利用资本形成总额来代替物质资本变量，而有的研究者是利用资本存量来代替物质资本变量，至于那种选取更能真实反映物质资本投资有待学着们的研究;同时在数据的采集过程中，有的数据存在缺失等状况，所以研究出来的结论也有可能有所偏离实际。

参考文献:

［1］曹丰，黄淑芬，许健榕.基于C-D生产函数的电力消费与经济增长关系研究［J］.海南大学学报:人文社会科学版，2012，30 (2) : 104-106

［2］金福良，李谷成.农村基础设施投资对农村经济增长影响的实证研究——以湖北省为例［J］.华中农业大学学报:社会科学版，2012(6) : 37-38

［3］SOLOW R.A Contribution to the Theory of Economic Growth［J］.Quarterly Journal of Economics，1956，70(1) : 65-94

［4］罗国旺.基于横纵因子分析和C-D生产函数的经济增长研究［J］.重庆师范大学学报:自然科学版，2014，31(1) : 118-122

［5］何剑.计量经济学实验和Eivews 6.0使用［M］.北京:中国统计出版社，2010

［6］KAO C.Spurious Regressions and Residual-based Tests for Cointegration in Panel Data［J］.Journalof Econometrics，1999，90: 41-44

［7］罗国旺.基于FAHP的重庆大学城“绿色大学”评价［J］.重庆工商大学学报:自然科学版，2013，30(6) : 70-73

Empirical Study on the Contribution of
Residents’Consumption to Short-term Economic Growth

LUO Guo-wang，PU Hao
(School of Mathematics and Computing Science，Zunyi Normal University，Zunyi 563002，China)

Abstract:Based on the theory of production function，the contribution rate of the residents’consumption variables on short-term economic growth is studied.According to the panel data of 1999—2008 in the West，the following point fixed effects model is set up on terms of time as influencing factor to research the promotion of economic growth by the residents’consumption in western China.The results show that the influence of residents’consumption on economic growth is increasing return of scale，and the contribution rate of residents’consumption to economic growth presents a gradually increasing trend.

Key words:household consumption expenditure; unit root test; co-integration

中图分类号:F224.12

文献标识码:A

文章编号:1672－058X(2015) 06－0030－06

doi:10.16055/j.issn.1672－058X.2015.0006.006

收稿日期:2014－10－07;修回日期: 2015－01－04.

作者简介:罗国旺(1986-)，男，贵州人，助教，从事系统优化理论、统计及经济系统分析方向研究.