“上下呼应，沟通你我”——例谈综合题的小问设计

☉江苏省如皋市实验初中 徐相柱

“上下呼应，沟通你我”
——例谈综合题的小问设计

☉江苏省如皋市实验初中 徐相柱

中考综合题的解题研究、命题研究一直都是很多同行关注的热点，特别是全卷的最后一题，命题组在设计时更是匠心独运，苦心经营，从而带来很多命题考查功能之外的试题立意、教学指向.当然也有个别考题出现了一些美中不足的现象，这在文1、2中得到商榷和改进，这种本着命题研讨的精神而开展的教研活动是十分难得的，值得我们学习.下面也列举两个题例，根据个人喜好也做些赏析或改编，就教于大家，期待批评.

一、题例及改编

题例1（2015年1月江苏省某市某校七年级上学期复习卷）数轴上，点A表示-3，点B表示5，点P表示数p.当AP=10BP时，求p的值.

思路分析：成功求解这道题有两个难点，一是分类讨论，即点P在线段AB上或AB的延长线上；二是根据数轴上两点之间的距离列出方程.

命题商榷：考虑到这道习题的难点分解，可以将问题做如下的分步设问，使得不同的学生在这道习题上都能取得相应的得分，从而追求更好的信度、效度与区分度.

命题改编：数轴上，点A表示-3，点B表示5.

（1）从A点出发，点在数轴上向右移动4个单位到达C点，则点C表示的数是_____，BC=_____.

（2）线段AB上有一点P，PA=k·PB，点P对应的数是p.

①当k=1时，p=_____；

②当k=3时，p=_____；

③p=_____（用含k的式子表示）.

（3）数轴上有一点N，当AN=10BN时，求点N所对应的数n.

解法提示：（1）1，4.

（2）①当k=1时，点P恰为AB的中点，于是对应着上一个问题，即此时点P位于（1）中的点C处.

②当k=3时，点P为线段AB的四等分点之一，容易求出此时BP=2，于是p=3.

③从绝对值几何意义、线段角度可以列出方程，p+ 3=k（5-p），解得p=

（3）与（2）相比，从“线段”到“数轴”，点N也就是上一问中的P，“10”就是上一问中的“k”，还是从两点之间的距离来构造方程处理较好些，而且需要分两种情况讨论.

第一种情况，点N在线段AB上，10（5-n）=n+3，解得n=

第二种情况，点N在线段AB的延长线上，10（n-5）= n+3，解得n=

题例2（2014年广东省广州市，第24题，14分）已知平面直角坐标系中两定点A（-1，0）、B（4，0），抛物线y= ax2+bx-2（a≠0）过点A、B，顶点为C，点P（m，n）（n＜0）为抛物线上一点.

（1）求抛物线的解析式和顶点C的坐标.

（2）当∠APB为钝角时，求m的取值范围.

思路简述：简要给出第三问的思路，结合第二问的求解，强化条件“若m＞当∠APB为直角时”得点P的坐标为（3，-2）.构造图1分析.

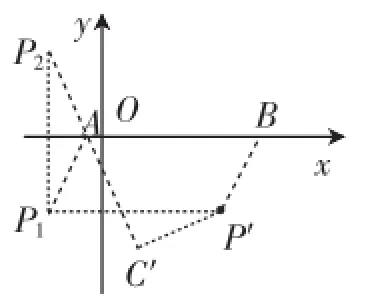
图1

设存在一个图形满足题意，此时C、P相应平移到C′、P′处，将点P′向左平移5个单位长度到P1处，作P1关于x轴对称的点P2，此时连接P2C′，应该恰好经过点A，才是符合要求的平移状态.

命题商榷：求解第二问时已经获得直角位置，进一步分析钝角的状态；而第三问却利用所谓的强化条件让学生倒过去，重拾这个直角位置，这与综合题各个小问之间“一步一步向上走”的命题取向有所偏离.此外，作为这道综合题最难的第三问，还有两个难点：难点之一，在于如何将其中一个点平移后利用“将军饮马”模式实现定位作图；难点之二，定位作图出来后，能否顺利解出答案也会阻拦不少学生，因为运算较繁，惜时如金的考场，挑战了学生的计算能力，导向“多思多算”的境地，值得商榷.

变式改编：如图2，平面直角坐标系下，抛物线y=ax2+bx-2（a≠0）经过点A（-1，0）、B（4，0），顶点为C.

（1）求抛物线的解析式和顶点C的坐标.

（2）设抛物线与y轴的交点为D，连接AD、BD，求证：AD⊥BD.

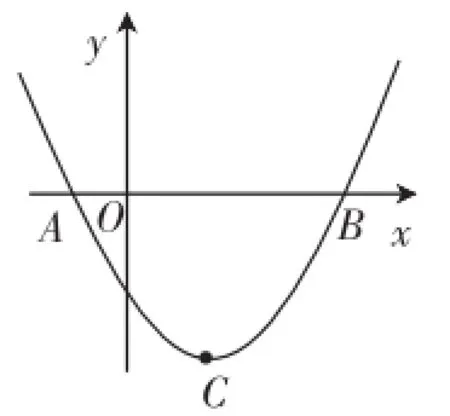
图2

（3）点P为抛物线在第四象限内一点，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜）个单位，点

C、P平移后对应的点分别记为C′、P′，是否存在t，使得首尾依次连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由.

改编意图：与原题相比，给出草图、改变第二问，使得入口较原题更宽，而且第三问删减无关旁枝的干扰（如点P（m，n）（n＜0）为抛物线上一点，若m＞，当∠APB为直角时），直接给出点P为抛物线在第四象限内一点，条件是等价的.当然，最后一问保持了原貌，读者不妨参与优化，笔者思考很久，但未能使运算量减少“.少算多思”是命题的一种追求.

二、进一步的思考

1.较难综合题的设问宜渐次生长、引导参与

我们知道，较难的综合题常常所占的分值也较大，如果这样的习题只有一个较难设问（如上文题例1），则容易造成更多的学生在考场上简单放弃，从而造成试题在区分度、信度上的不足.这时将问题重新改编，从一个十分简单、好懂的基础条件出发，渐次生成、变式拓展，引导更多学生参与应答，而最后的问题又要真正起到“把关”作用，让一道题目就能使不同的学生的解题能力得到很好的区分.

2.不同小问之间需要加强关联、沟通你我

当前很多中考综合题下面的几个小问题的设计多以并列式问题为主，如题例2这样，三个小问之间并无递进式关系，但是它们的求解思路、后一问的解题念头的来源却又需要借助上一问的思路启发，像这种命题设计技术就是注重关联.此外，如题例1的改编那样，第一问中的点C成为下一问中的点P，而最后一问中的N点沟通着上一问中的P，这种关联前后、沟通你我的设计都需要精心构思，待到习题讲评时也需要引导学生思考和体会.

1.邬吉利.一类“伪坐标系”考题的评析与商榷［J］.中学数学（下），2014（8）.

2.朱月祥.改编考题为研讨，追求简洁重关联［J］.中学数学教学参考（中），2014（12）.

3.贺信淳.从多角度审视一道中考试题说开去——谈对初中数学教育现状之惑［J］.数学通报，2013（12）.