敢于向错误说“NO”

☉山东省沂源县实验中学 崔春近

敢于向错误说“NO”

☉山东省沂源县实验中学 崔春近

笔者在平时的教学或教研活动中发现课本中的一些习题答案，甚至中考试题及其参考答案，有时也存在错误，如何引领学生面对这些错误，怎样处理这些“权威”出现的问题，笔者认为应该将错误变为教学新的资源，将错就错，让学生在对抗错误的过程中理顺问题出现的来龙去脉，敢于向错误说“NO”.下面，笔者结合几种错误的类型谈谈自己的粗浅做法.

一、“一厢情愿”型

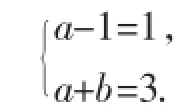
阅读上面材料，解答下列问题.

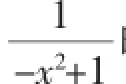
教师：此题的分析有没有问题？

课堂中教师故意根据参考答案的求解思路给学生分析，等待学生提出疑议.

众学生一脸惊异地看着学生1，想尽快地听到学生1的分析.老师也疑惑地看着学生1能够给大家一个“惊喜”.

教师：“-x2+1的最大值为1”对吗？

众学生：对.因为在原题中并没有限定x的范围，所以-x2+1≤1且不为0.

同学们通过特值等方法发现了大体的分类.

学生4：我们应该分0＜-x2+1≤1和-x2+1＜0两种情况.

教师：为什么这样分呢？

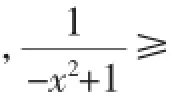
学生5：参考答案把-x2+1的范围限定为-x2+1＞0了.

教师：同学们分析的非常好！现在，我们把数的范围扩展到了实数，所以求倒数时也一定要分情况讨论噢！

学生6：原来中考试题的答案也有错误啊！

教师：谈一谈你的收获.

学生7：在求倒数时一定要分大于0和小于0两种情况.

学生8：中考试题的参考答案也有错误，我们不能太相信答案.

学生9：在学习中要有质疑的精神，尽信书则不如无书.

教师：同学们认识的很深刻，对于本题的探究，老师认识的也不到位，差一点让错误蒙蔽，因此，在平时的学习中，我们必须治学严谨，敢于向错误说“NO”.

教师：让我们为表现突出的同学鼓掌，为我们的共同进步喝彩吧！（教室中不约而同地响起了同学们的掌声）

二、“画蛇添足”型

例2（2011年广州湛江数学中考试题第27题）如图1，在Rt△ABC中，∠C=90°，点D是AC的中点，且∠A+∠CDB=90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E.

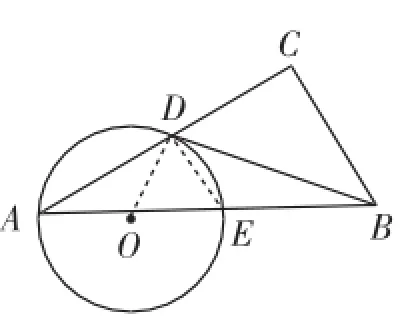
图1

（1）求证：直线BD与⊙O相切；

（2）若AD∶AE=4∶5，BC=6，求⊙O的直径.［1］

题目分析：本题的难度不大，第（1）问没有问题，但在第（2）问的处理上却出现了分歧.

学生1：因为AE是直径，所以∠ADE=90°.又因为∠C=90°，所以∠ADE=∠C，所以DE∥BC，所以△ADE∽△ACB.因为AD∶AE=AC∶AB，所以AC∶AB=4∶5.又因为BC= 6，所以AB=10，所以AE=AB=5.

教师：大家说学生1解得好不好？

众生：好！

教师准备点评这一题目时，学生2的回答打破了课堂的平静.

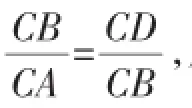
教师：大家说学生2解得对不对？

众生：对！没有问题.

真是一波未平一波又起，学生3站起来谈自己的解题思路.

学生3：我解出的答案和他们不一样.

教师：说一说你的思路.

教师：学生1、学生2、学生3的解析是不是都没有问题啊！

众学生：是.

教师：三种不同的思路，得到了三种不同的答案，问题在哪里呢？

众学生脸上一头雾水，不知所措.

教师：好！让我们分小组讨论探究，看哪个小组最先找到问题的答案.

同学们讨论很热烈，很快就有同学起来发言.

学生6：中考题也会有纰漏，中考题也不是我们想象中的那样权威.

教师：我们已经找到了问题的症结所在，同学们想一想我们该怎样修改呢？学生7（抢先回答）：老师，既然的值是一个定值，那么AD∶AE=4∶5这一条件就是错误的，改为=就可以了.所以可以直接把AD∶AE=4∶5这一条件删掉.

教师：很好，我们只能这样改吗？

教师再一次把问题抛给学生.同学们带着老师的问题开始讨论，过了一段时间，有学生起来谈自己的思路.

学生8：我们通过题干就可以得出

学生9：我们也可以把题干中“点D是AC的中点”这一条件去掉.

教师：这样还能不能求出答案？

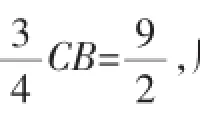
问题在讨论中渐渐落下了帷幕，在一题多解中，学生找到了错误的根源，明白了问题出现的原因，更重要的是在探究讨论的过程中，学生锻炼提升了自己分析问题、解决问题的能力.

三、“考虑不周”型

例3如图2，已知直线y=（k-2）x+ k不经过第三象限，则k的取值范围是（）［.2］

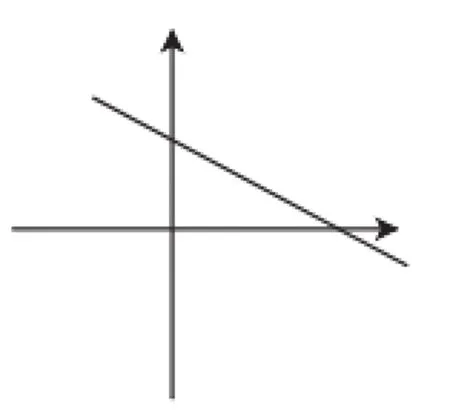
图2

A.k≠2B.k＞2

C.0＜k＜2D.0≤k＜2

问题分析：本道题是学生在刚刚学习了一次函数之后的一道练习题，很多学生由于思维定势，不加思索地认为直线y=（k-2）x+k就是我们所学习的y=kx+b（k≠0，k，b为常数），不经过第三象限就是经过一、二、四象限，图像如图2所示，所以k-2＜0，k＞0，答案选择了C.这主要还是学生对教材的基本知识点掌握不是很熟练，没有真正掌握正比例函数也是一次函数，当然这也是命题者着重要考查的知识点.本题意在考查学生对一次函数图像的掌握运用能力，同时也想通过本题考查学生全面分析问题的能力，命题者在选择项上设置了“陷阱”，具有一定的迷惑性.

进行课堂讨论，学生很快想到了另一种情况.

学生1：当k=0时，也就是直线y=（k-2）x+k为正比例函数时，y=-2x也符合题意（不经过第三象限），因此，k=0也可以，所以答案选D.

老师：很好，学生1能够真正掌握正比例函数也是一次函数这一知识点，注重了分情况讨论，考虑问题十分全面，希望做错的同学要提高认识，做好反思整理，在今后的做题中要提高警惕.

看着出错的同学也有恍然大悟的感觉，教师也感觉很幸福，在讨论中学生领会了自己出错的原因.本想结束本题的讲解时，学生2的回答又让课堂起了波澜.

学生2：此题没有答案.

众学生一脸的茫然，就连授课的教师也感觉到很意外，也想听一下学生2有何高见.

学生2：当k=2时，直线y=（k-2）x+ k变为直线y=2，而y=2是平行于x轴的一条直线（如图3所示），也符合题意.

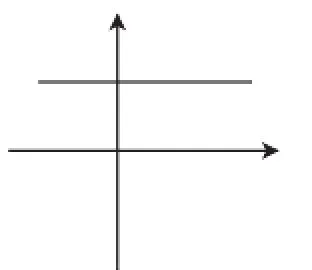
图3

学生3：我们这一章学习的是一次函数，一次函数的定义就是形如y= kx+b（k≠0，k，b为常数），所以很明确k≠0，而当k=2时，直线y=（k-2）x+k就不是一次函数了.

学生2：（马上反驳）本题只是说直线y=（k-2）x+k，而并没有强调是一次函数y=（k-2）x+k，所以k=2是符合题意的.

在讨论中教师感觉学生明白的更多了，通过师生共同总结得出结论：此题的命题者考虑不周，导致了题目的不严密，原题若改为：

已知一次函数y=（k-2）x+k的图像不经过第三象限，则k的取值范围是（）.

A.k≠2B.k＞2C.0＜k＜2D.0≤k＜2

此时答案就是D.若不改动，原题的答案就应该是0≤k≤2.

教育的过程就是一个不完美的人引领着、另一个不完美的人追求完美的过程，我们永远走在“趋于完美”的路上，而达到“知行合一”需要一个过程（尚川语）.所以，教学的过程是不断探究的过程，是突破思维定势、大胆创新的过程.

四、教学启示

进入幼儿园之前，儿子最喜欢说的话是“爸爸，我觉得……，我认为……，我发现……”，有自己主见的东西很多，上完幼儿园后，孩子还保留着这份天真，但从小学三年级后，孩子渐渐地学会了“顺从”，像如“我们老师说了……，学校规定……”的话多了，老师的“权威”在孩子心中树立起来，有些时候，这份“权威”不利于孩子的成长.在平时的教学中，笔者认为应鼓励学生有自己的思想，敢于向问题挑战，对于中考试题及答案中出现的错误，要有质疑求真之胆.让这些错误成为学生探究的新平台，树立让学生走“弯路”就是让学生体验探索新知旅程的理念，实现在“对抗”错误的过程中“积累”经验，在“求真”的过程中，让学生的思维之花绽放.

1.李海涛.由一道中考错题教学引发的思考［J］.中小学数学（初中版），2013（9）.

2.崔春近.失之毫厘谬以千里［J］.中学数学杂志，2012（12）.