基于知识梳理的“普惠”复习——谈中考首轮复习课的设计

☉江苏省如皋经济开发区袁桥初级中学 顾亚琴

基于知识梳理的“普惠”复习
——谈中考首轮复习课的设计

☉江苏省如皋经济开发区袁桥初级中学 顾亚琴

近期，笔者参加了如皋市的中考复习研讨会，并观摩了一节题为“根据已知条件求二次函数的解析式”的复习课.教者以“求二次函数的解析式”作为课堂教学主线，精心设计配套例题，通过学生的自主解答和师生的互动交流，很好地梳理了“用待定系数法求二次函数的解析式”这一基础知识.现结合这节复习课谈谈笔者对中考首轮复习课设计的一些思考，希望对您有帮助.

一、课例及简析

1.教学目标分析

“会用待定系数法求二次函数的解析式”是教者给这节课设计的唯一一个教学目标.二次函数的解析式包含三种形式，分别是“一般式”y＝ax2+bx+c（a≠0）、“顶点式”y＝a（x-h）2+k（a≠0）和“交点式”y＝a（x-x1）（x-x2）（a≠ 0）.近几年的任何一份试卷中，至少会考查其中的一种形式.与此相关的考题一般是综合题的“前奏”，是综合问题生成的情境，题目难度并不大.所以在首轮复习时，教者将“会用待定系数法求二次函数的解析式”作为课时目标是较为适合的.

2.教学过程简录

活动1：以图理知，回顾二次函数的解析式.

题目如图1，抛物线经过点A、B、C、D，其中D为抛物线的顶点，请根据图中的数据求出这条抛物线的解析式.

学生活动：求图1中抛物线的解析式，并在小组中交流.

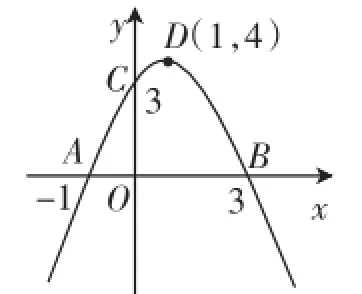
图1

5分钟后，小组交流结束.教师组织学生在全班交流，并板书学生给出的两种解析式y＝-（x-1）2+4，y＝-（x＋1）（x-3）.然后追问：这条抛物线的一般式是什么？你能将这三种形式转化吗？学生给出“一般式”，并尝试将这三种形式互相转化.最后，在师生互动中，梳理并板书二次函数的解析式的三种形式.

设计意图：在教者给出的这幅图中，抛物线上一共有四个点，分别是A（-1，0）、B（3，0）、C（0，3）、D（1，4）.设置这样的问题情境，让学生从图像中捕捉信息，培养了学生的读图能力和转化能力.教者给出了四个点，并且这四个点较为特殊，点A和点B是抛物线与x轴的交点，而点D是抛物线的顶点.所以不同的学生可能会从不同的角度思考求解的方法，因而也会给出“求抛物线的解析式”的不同方法.有的同学可能会用顶点式求解，也有些学生会用交点式求解，一些较为保守的同学则会用一般式求解.这些求解方式是“三种形式互相转化”探究活动的基础，也是学生优选解析式解题的基础.由此可见，“以图理知”不仅能够梳理二次函数的解析式，还能为后续学习提供教学资源.

活动2：自主求解，归纳优选求解的策略.

学生活动：自主解答下面的三道例题，并在小组中交流用到的知识和方法.

例1已知：直线y＝-3x＋3与坐标轴交于A、B两点，经过A、B两点的抛物线y＝ax2＋bx＋c过点（-2，3），求此抛物线的解析式.

例2如图2，抛物线y=ax2+bx+c经过A（-3，0）、C（0，4），点B在抛物线上，CB∥x轴，且AB平分∠CAO.求抛物线的解析式.

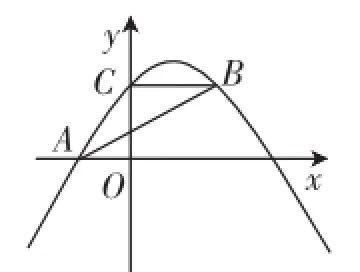
图2

例3已知抛物线y=ax2+bx+c经过点（0，3），对称轴为直线x＋2＝0，且在x轴上截得的线段的长度为2，求此抛物线的解析式.

学生自主探究，教师巡视指导.20分钟后，小组交流结束.教师组织学生交流，并就解题中用到的知识和方法进行了认真的梳理.在交流过程中，教师对学生得出的点特别关注，要求他们说出这些点与坐标轴和抛物线的位置关系，并反复强调“要结合点的特点，选择合适的解析式求解”.针对学生给出的“一题多解”，教师指出“在求点的坐标和对称轴时，要充分利用抛物线的对称性”.在投影展示并交流点评了几位同学的求解过程后，教师让学生根据讲评的收获自主订正.最后，教师将这三道例题的规范求解过程进行了投影展示，让学生对比矫正.

设计意图：例题的编排是巧妙的，三道题目都指向了“求此抛物线的解析式”.从教学过程看，无论是学生的自主探究，还是互动交流，都围绕在教学主线之上.三道例题，解法各异，是对三种不同形式解析式的深度应用.很明显，“方法优选”是教者设计这个活动的主要目的.为了顺利让学生找到“方法优选”的技巧，教者组织学生进行了自主探究，并通过点评交流及范例矫正，生成了一些个性化求解策略.其中，抓对称性求点和析点选解析式的策略，均是教者的期待，对学生今后解题均会产生巨大的影响.当然，这些策略向学生个体解题行为的转化非朝夕之功，但只要教师在教学中不断反复地坚持训练，其内化的进程必将会加快，成功转化是迟早的事.

活动3：课堂小结，促进知识网络的建构.

教师提出让学生课堂小结的要求，让学生从知识、方法和注意点等方面小结全课的收获.学生立即在小组中展开交流，热烈的交流让学生实现了“颗粒归仓”.在小组交流结束后，教师组织学生在全班进行交流，学生的陈述让“优选解析式”的策略及应用注意点在全班得到共享，数形结合思想的交流更是提升了小结的档次，让学生不仅在知识上有了收获，还在数学思想方法上有所斩获.这些成果的小结与梳理，将原来凌乱的知识和思想方法，逐步并入到学生已有的函数知识板块之中，提升了学生分析问题和解决问题的能力.

设计意图：小结是课堂教学的重要环节，但我们决不能让小结流于形式.在中考首轮复习课上，小结环节同样不可缺少，与新授课一样，它同样能完善学生的认知网络.二次函数的解析式的求法，是“用待定系数法求解析式”的重要组成部分.与初中阶段的其他函数相比较，用待定系数法求解析式的过程几乎是一致的.最大的差别，就在于多了一个优选的过程.小结，让学生体会到优选的重要性，对优选的技巧有了较深的认知，同时，也让学生体会到抛物线的对称性的应用价值，对数形结合思想有了更进一步的认识.课堂小结，让求解析式不再是一个孤立于点的坐标之上的解方程组问题，而是与数形结合密不可分的综合型问题.

二、中考首轮复习课设计的思考

因教学时段的不同，中考前的复习常有首轮、二轮、三轮之分.不同轮次的复习，教学的侧重点也不同，因而其教学内容也有着明显的差异.笔者所听这节课就是一节首轮复习课，教者的设计紧贴学生的认知需求，为学生梳理旧知建构知识网络设计了很好的题组和探究活动，充分体现了中考一轮复习“基础性”的特点.

1.指向基础知识，力求全面覆盖

首轮复习应指向初中学段的所有知识，让这一学段的每一个知识点都有“登台表演”的机会.所以设计首轮复习课，应从最基础的知识入手，让与课时教学主线相关联的所有基础知识、基本技能、数学思想方法和活动经验都呈现在教学过程之中.这样做的目的，能有效避免一些“边角”知识因复习不到位，成为学生应试的“盲区”，导致在中考中出现不必要的失分.所以首轮复习课上，我们应通过设置有效的探究例题和问题情境，让学生在自主探究与合作交流中唤醒初中阶段学习的各种知识，使之在回顾交流中关联融合、结成网络.以笔者所听这节课为例，与二次函数相关的考题众多，绝大多数难度都不小，如果将这些题目不加调整地直接进入教学，教学重点不能凸显自不必说，就学生求解能普遍到达的程度，这些综合型问题作为例题出现也是不适宜的.所以在设计时，教者设计了“求二次函数的解析式”这一教学主线，并围绕主线精心设置了与之匹配的例题.从教学的进程来看，教师始终着眼于与二次函数的解析式相关联的基础知识的梳理，三种不同形式的解析式在学生求解和交流点评中反复运用，教学效果还是很不错的.

2.指向全体学生，强调全员普惠

知识的全面覆盖是首轮复习的追求，学生的全面覆盖则是首轮复习课的另一追求.在教学设计时，我们不仅要关注知识回顾的面，还要关注学生参与的面，要让每一名学生都从复习中受益.所以设计中考首轮复习课，应从学情分析入手，将教学设计在学生能够承受的基础之上.历经三年的初中数学学习，学生在数学认知上的差异不可避免，不同的学生在数学上已经得到了不同的发展，所以中考复习课如何实现有差异的教学确实值得探讨.笔者认为，作为首轮复习课，我们应尽可能地“忽略”这些差异，设计出“优劣兼容”的数学课堂，让每一名学生都能参与进来.根据多年教学的经验，首轮复习课的例题一般以中档题为主，这样的例题后进生“跳一跳”能够解决，为让优等生“吃得饱”，我们可以为他们准备一些与课时主题有关的“备用题”.上面的案例中，教者对中考试卷一些综合题进行了有效的分离，简化了求解的情境，让综合问题的难度降低了不少.从改编后得到的三道例题来看，难度并不大.在经历这里“以图理知”后，绝大多数学生都能将所回顾的几种解析式应用到问题分析与解答之中，对课时教学目标的达成是十分有利的.

3.指向自主求解，强化个性体验

学生不仅是学习的主体，也是中考应试的主体.在常态教学中，我们也应让学生的考试主体地位凸显出来.让学生经历完整的自主求解过程，体会到解题过程的“酸甜苦辣”，这对中考首轮复习显得尤为重要.“厚积方能薄发”，只有在学生经历了最基础知识的不断累积后，才可能让这些知识在今后的问题化解中精准叠加，形成一些综合性问题的求解思路.所以首轮复习时我们应从学生独立求解出发，让学生找到自己知识和能力上的“不足”，形成自我弥补的积极状态，从而推动复习走上快速通道.在上面的这节复习课上，解三道例题是学生的个体行为，虽然其间也夹杂着或多或少的一些小组内交流和全班交流，但它们所起的作用是有限的，是无法替代自主解答的.只有让学生经历了解对或解错并纠错的过程，在今后的问题解决中，他们才能形成自觉地提取与应用与问题情境相关联知识的意识，才能主动养成规避错误的习惯.这样的自主解答无疑是个体解题经验积累的有效保证，值得关注.

三、写在最后

中考复习，因所处的时段不同教学任务也不同.首轮中考复习，应以基础知识的梳理为主要目标，力求通过对不同版块的基础知识的扫描，将凌乱的学段知识“有序摆放”、有效关联，完善、充实已有的认知网络.这样的复习定位，保证了“边角”知识不会被遗漏，同时，便于学生在今后解决数学问题时，从网络化的知识框图中提取必需的知识和技能，实现有利于问题解决的知识与技能的叠加.所以首轮复习课的设计应以学情为起点，以课标和考纲为参照，立足于学生的认知“低点”，从满足全体学生回顾旧知的需求出发，选择与课时教学任务匹配的“原题”，结合不同层面的学生的认知状况进行适度调整，从而形成“普适度”极高的教学例题.有了这样的设计起点，加之教师对教学过程的精心设计，实现基础知识的梳理与知识网络的建构自不在话下，提升学生分析问题和解决问题的能力也应该在情理之中了！

1.印冬建.突出核心主线追求有效教学——谈初中数学有效备课的做法与思考［J］.中学数学（下），2014（1）.

2.廖小芳.用待定系数法求二次函数解析式的几种情形［J］.中学教学参考，2011（9）.