新定义题破题策略与命题商榷——以北京市海淀区初三第一学期测试卷第25题为例

☉山东省莒南县岭泉镇初级中学 闫守范

新定义题破题策略与命题商榷
——以北京市海淀区初三第一学期测试卷第25题为例

☉山东省莒南县岭泉镇初级中学 闫守范

众所周知，北京市中考数学卷已连续多年在最后一题的位置上设计原创的新定义题，这种命题导向引发了其他地区新定义题型的命题跟进，“上有所好，下必迎合”，在应试复习仍然严重的当下，特别是北京市各区的模拟考卷常常也在关键位置设计出新定义考题，为考生提前做好预热.本文以新近一道北京市海淀区初三第一学期期末考试中的最后一题为例，讲解破题策略，最后再由这道习题出发，谈谈这类问题的命题商榷意见，与大家研讨.

一、新定义题的破题策略

例1（2014-2015年北京市海淀区初三第一学期期末卷）在平面直角坐标系xOy中，设点P（x1，y1），Q（x2，y2）是图形W上的任意两点.

定义图形W的测度面积：若|x1-x2|的最大值为m，|y1-y2|的最大值为n，则S=mn为图形W的测度面积.

例如，若图形W是半径为1的⊙O.当P、Q分别是⊙O与x轴的交点时，如图1，|x1-x2|取得最大值，且最大值m= 2；当P、Q分别是⊙O与y轴的交点时，如图2，|y1-y2|取得最大值，且最大值n=2.则图形W的测度面积S=mn=4.

图1

图2

（1）若图形W是等腰Rt△ABO，OA=OB=1.

①如图3，当点A、B在坐标轴上时，它的测度面积S= ________；

图3

图4

②如图4，当AB⊥x轴时，它的测度面积S=________.

（2）若图形W是一个边长为1的正方形ABCD，则此图形的测度面积S的最大值为________.

（3）若图形W是一个边长分别为3和4的矩形ABCD，求它的测度面积S的取值范围.

思路讲解：

第一步，理解定义好起步.

初读所谓的“测度面积”有些晦涩，不太好理解，这时需要认真阅读题目所配例子，那个圆的图形测度面积可以加深对新定义的理解.再进入第（1）问第①小问的求解，△AOB的三个顶点的坐标分别为（1，0）、（0，0）、（0，1），这样，|x1-x2|的最大值m就是AO的值1，|y1-y2|的最大值n是BO的值1，于是“测度面积”S=mn=1.

第二步，并列问题实递进.

第（2）问看似与上一问无关，并列式设问，其实只是把第（1）问中的等腰直角三角形补成一个正方形继续探究，分两种情况思考：

如图5，|x1-x2|的最大值m就是正方形的边长1，|y1-y2|的最大值n是正方形的边长1，于是“测度面积”S=mn=1.

如图6，|x1-x2|的最大值m就是正方形的对角线的长，|y1-y2|的最大值n是正方形的对角线的长于是“测度面积”S=mn=2.

图5

图6

第三步，拓展生长需挑战.

第（3）问从上一问正方形变式为矩形，问题也改为求“测度面积”的范围，可以分别思考其上限、下限.

以下给出网络上流行的所谓“参考答案”：

不妨设矩形ABCD的边AB=4，BC=3.由已知可得，平移图形W不会改变其测度面积S的大小，将矩形ABCD的其中一个顶点B平移至x轴上.

当顶点A、B或B、C都在x轴上时，如图7和图8，矩形ABCD的测度面积S就是矩形ABCD的面积，此时S取得最小值，且最小值为12.

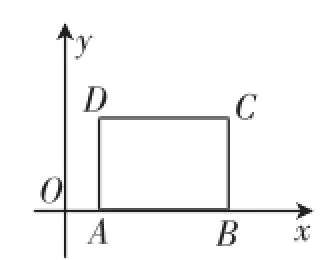
图7

图8

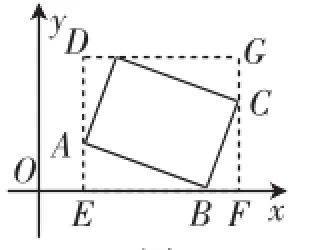
图9

上面通过分类思考图7、图8两种情况，它们的共同点就是矩形的两边分别与坐标轴平行（含重合）时，这样矩形ABCD的测度面积S就是矩形ABCD的长、宽的积.

然而将矩形的位置旋转一定的角度后，如图9，当顶点A、C都不在x轴上时，需要构造辅助线进行思考，可以过点A作直线AE⊥x轴于点E，过点C作直线CF⊥x轴于点F，过点D作直线GH∥x轴，与直线AE、CF分别交于点H和G，则可得四边形EFGH是矩形.

当点P、Q分别与点A、C重合时，|x1-x2|取得最大值m，且最大值m=EF；

当点P、Q分别与点B、D重合时，|y1-y2|取得最大值n，且最大值n=GF.

要注意，这里分别探究EF、GF的最大值意义并不大，而需要整理思考图形W的测度面积S=EF·GF的最大值.

因为∠ABC=90°，所以∠ABE+∠CBF=90°.

因为∠AEB=90°，所以∠ABE+∠BAE=90°，所以∠BAE=∠CBF.

设AE=4a，EB=4b（a＞0，b＞0），则BF=3a，FC=3b.

在Rt△ABE中，由勾股定理得AE2+BE2=AB2.

所以16a2+16b2=16，即a2+b2=1.

易证△ABE≌△CDG.所以CG=AE=4a.

解后反思：现在来反思上面的求解，容易发现，最后一问关于测度面积的最大值是极具挑战的，主要难点有两处，第一，能否及时将问题分解为三种情况思考，即图7、8、9的情况；第二，对于图9情况的探究，能否引入恰当的参数，并对“12+25a进行高超的配方变形，这事实上也超越了初中阶段数式变形的要求，一般学生在考场上是难以顺利完成的.

让我们认真思考第（1）（2）问解题之外能积累的一些经验，是不是可以猜想并确认如下性质：平移图形W不会改变其测度面积S的大小，只是在旋转时会改变，而且当矩形的边分别与坐标轴平行时，测度面积S会取得最小值；而当矩形的一边与坐标轴成45°角时，测度面积会取得最大值.

图10

二、后续思考

如前所述，由于像北京市中考卷常常在最后一题这样的位置设计新定义题的风向标作用，很多地区也纷纷效仿，对新定义题过分偏好，出现很多不够恰当的新定义题，比如简单地将高中阶段的某个数学概念、公式或性质下放到中考试卷；或者个性化地命名所谓的新概念，造成试题的信度、效度不好，以下再围绕上面这道考题商榷两点：

1.“新定义”是否严谨

该考题的最上面一句话“在平面直角坐标系xOy中，设点P（x1，y1），Q（x2，y2）是图形W上的任意两点”.而“定义图形W的测度面积：若|x1-x2|的最大值为m，|y1-y2|的最大值为n……”时，容易让人误解为y1与x1是严格对应的，那样的话，当“若|x1-x2|取得最大值m”时，而|y1-y2|只能跟前面有一个唯一对应的值，又怎能取得最大值呢？

2.拓展生长问题的解法不能“超标”设计

第（3）问的“网上流传的解法”如果是命题组提供的话，那么对于超高要求的配方变式显然属于“超标”设计，在现行各种教材上也难找到相对应的数式变形的要求，这样的命题导向将数学引向繁难，值得商榷.如果采用后续反思过程中提及的将矩形旋转45°的方法，又有一个麻烦，是否所有矩形的所谓测度面积都是旋转45°后，测度面积获得最大？理由何在？这只是从前两问猜想和发现的一种经验，可见深入思考这个“经验问题”还是有积极价值的.

1.周艳娟.关于试题人文价值的另类思考［J］.中学数学（下），2015（1）.

2.刘东升.并列式问题与递进式求解［J］.中学数学教学参考（中），2012（8）.