对三角函数积分表的一点补充

周兰兰

摘 要 本文从三角函数积分表缺少的一些公式入手，逐步进行推导，并在过程中熟悉求不定积分的一般方法。

关键词 三角函数不定积分 根号 绝对值

中图分类号：O1-647 文献标识码：A DOI：10.16400/j.cnki.kjdks.2015.02.013

Supplement for Trigonometric Integral Table

ZHOU Lanlan

（College of Information Science & Technology， Hainan University， Haikou， Hai'nan 570228）

Abstract This article starts form missing some trigonometric formulas standings， gradually derived and general method familiar indefinite integral in the process.

Key words trigonometric indefinite integral; radical sign; absolute value

在目前可找到的三角函数积分表中，基本上都缺少和其他一些更加复杂的形式，显然，并不是取任意值的时候都可以将其导出成初等函数的形式，但是至少可以取一些比较简单的值进行计算。如 = 0， = 0这种特殊情况，即求不定积分，可以得出其不能以初等函数表示，此处不予证明。

考虑到可以变换成（）∧2的特殊形式，不妨令 = 1， = 1进行运算。所以原式可以化成∣∣的形式，于是本题实质上转化为求∣∣的不定积分，那么求∣∣的不定积分是否可以继续化简，又是否是初等函数的形式呢？下面将进行讨论。

例：求不定积分：∣∣

解：令 （） = ∣∣，显然 （）在上是连续的，所以其必定存在原函数。

按照常规方法先把∣∣用分段函数表示出来：

分别对这两段求原函数，当（，]时，一个原函数为（） =  + ，当（，]时，一个原函数为（） =  + ，此时要保证原函数在 = 和 = 上连续即可，于是列出方程 = 时， + =  + ，由 = 1得 = 2。

此时会有部分同学直接得出答案，原函数

但是，如果继续 = 时的方程，就会由 = 得到 = +2，很显然，不存在固定的常数，使这两个式子同时成立。

于是就会遇到一个问题，当通过两种不同的点计算得到的常数的值不同时，应该如何计算？

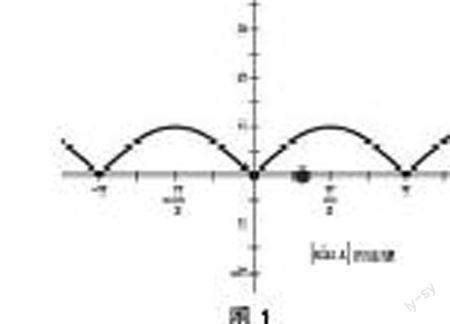
所以我们需要再次审视一下得出的结论：不存在固定的常数，使这两个式子同时成立。什么是固定的常数？难道还存在不固定的常数能够满足这个式子吗？的确，存在不固定的常数，可它为什么不固定，它是因为什么变化的呢？让我们再回过头去看当初的函数 （） = ∣∣，这个函数在上显然是恒大于等于0的，也就是说，它的原函数（）在上是单调增的，并且由于 （） = ∣∣是一个周期函数，所以（）在上是没有界的（图1）。

图1

而我们一开始求出的表达式

，

和都是有界函数，所以只能是这个不固定的常数，是无界的。而（）中的参数除了和，外，也只有了。在我们的思维中，三角函数中的绝大部分情况都是用来表示的取值范围，极少情况函数的表达式与有关。，到底和之间保持什么关系呢？很自然地，我们可以先猜测，与之间保持一次函数关系，因为这是我们最熟悉的一种形式，值得注意的是，对于点， + 与 + 的取值是相同的，而对于点，要表示同一个点的话， + 与 + 的取值不同。举个例子，要表示横坐标为的点，在（，]中， = 1;在（，]中， = 0。即 =  + ，  =  + 。然后分别将之代入一开始我们得出的方程： = ，即 = 1时， +  =  + 与，即 = 时， +  =  + 。联立可得

即该方程组对任意的和均成立。解之得 =  = 4，  = ，于是得出本题答案

解出后我们可以发现，∣∣的不定积分并不是初等函数。但是我们仍然可以在有限的区间上讨论该函数的性质。

图2是

（ = 0）

时一部分的图象，可以看出其是阶梯形变化的。所以可以对积分表进行补充：

同理可以通过求出∣∣的不定积分的方法来推出的不定积分。