基于MATLAB的高压腔电液压力伺服控制系统设计及仿真
, , ,
(燕山大学 河北省重型机械流体动力传输与控制重点实验室, 河北 秦皇岛 066004)
引言
随着我国核电事业的迅速发展,核电用管的需求也随之增加,为了满足核电用管的质量需求,超高压润滑拉拔机应运而生。
超高压润滑拉拔机就是将高压润滑技术与传统拉拔机相结合来改善拉拔机的润滑条件,从而生产出高质量的核电用管。其核心要求是高压油腔的压力恒定,但是在拉拔过程中随着拉拔管向外的运动,需要对高压腔进行补油,而补油的过程必然会造成高压腔内的压力变化。对此,采取电液伺服控制系统进行压力控制,保证压力恒定。
在工程上,电液伺服系统的设计一般包括以下主要步骤: ① 根据工程要求设计控制系统原理图; ② 确定系统的主要参数(系统压力、伺服阀规格、执行元件规格等); ③ 确定控制器参数,分析系统的动、静态特性是否满足要求[1]。在本研究中,运用MATLAB中的Simulink工具箱对压力伺服控制系统进行建模,通过仿真对控制参数进行确定,并对其阶跃响应、Bode曲线等进行分析,保证在钢管的拉拔过程中高压腔的压力恒定。
1 拉拔机的工作原理简介
高压润滑拉拔机液压控制系统包括:密封缸伸缩系统、线材升降系统、尾部芯棒位置控制系统、高压润滑腔压力控制系统等。这里主要研究高压润滑腔的压力控制系统。下面对高压润滑拉拔机的工作过程进行简单的介绍。
首先,启动液压泵,对液压系统进行预热。同时检查拉拔机是否处于停机位置。然后增压缸打油,将高压腔充满,手工将毛坯管料推入高压腔,同时芯头退至最后。模具下降,尾部顶冲缸控制芯头位置,密封缸贴紧密封,再次为高压腔充满油。拉拔小车开始拉拔,拔出50 mm后停下,高压腔升压到额定压力保压,再开始拉拔。根据电导通方式检测到管坯尾端通过后,估算出待剩余50 mm时,小车停止,高压腔泄压,再将剩余管料拉出即可。其结构简图如图1所示。
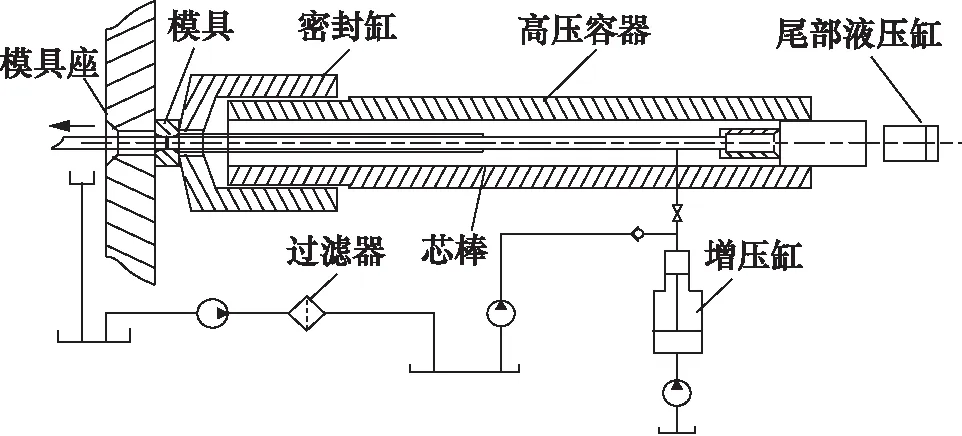
图1 高压润滑拉拔机结构简图
2 电液压力伺服控制系统的数学模型建立
由分析可知随着管坯的拉拔,高压腔内会产生压力变化,而高压腔的压力恒定又是整个拉拔过程必须满足的工艺要求,以此来保证管壁的光洁度等性能要求,因此必须对高压腔进行压力控制,下面将对高压润滑拉拔机电液压力伺服控制系统进行建模分析。其控制原理方框图如图2所示。

图2 压力控制系统原理方框图
2.1 伺服阀基本方程
伺服阀是伺服控制系统的核心元件,是电器元件与液压元件之间的桥梁。其应用的可靠性直接影响着整个伺服系统的控制精度[2]。
伺服阀具有非线性,但是可以在零位附近进行线性化处理,其线性化方程为:
QL=Kqxv-KcpL
(1)
式中:QL为伺服阀的空载流量,m3/s;Kq为流量增益,m2/s;Kc为压力-流量系数,m3/(s·Pa);xv为滑阀位移,m;pL为负载压力,Pa。
当伺服阀的频率较高时可将其传递函数表示为二阶振荡环节的形式:
(2)
式中:ωsv为电液伺服阀固有频率,rad/s;ζsv为电液伺服阀阻尼比。
伺服阀的流量增益为:
Ksv=QL/Imax
(3)
式中:Imax伺服放大器的最大输入电流,A。
计算可得Ksv=0.117。
伺服阀的样本曲线如图3所示。同时,根据伺服阀的样本曲线可以得到ωsv=816.4 rad/s,并取ζsv=0.5,带入式(2)即可得伺服阀的传递函数。
2.2 液压缸流量连续性方程
在对系统进行分析时通常会把非线性问题简化为线性问题,对于液压缸来说,在某个稳定工作点做微量运动时可近似为线性特性,可用线性微分方程来描述[3]。本研究液压系统中液压缸与伺服阀之间的距离很短,因此,可以忽略阀与缸之间的管道连接,这样也可以不计油液在管道中流动造成的压力损失;同时假定油液的体积弹性模量和油温为常数,且液压缸的泄漏为层流流动。则液压缸的流量连续性方程为:
(4)
式中:Ap为液压缸有效作用面积,m2;βe为油液有效体积弹性模量,Pa。
2.3 液压缸力平衡方程
液压控制系统中,负载特性直接影响动力元件的特性。系统的负载力一般有:惯性力、弹性力、黏性阻尼力[4]。则液压缸的输出力与负载的力平衡方程为:
AppL=mts2xp+Bpsxp+Kxp
(5)

图3 压力控制系统方框图
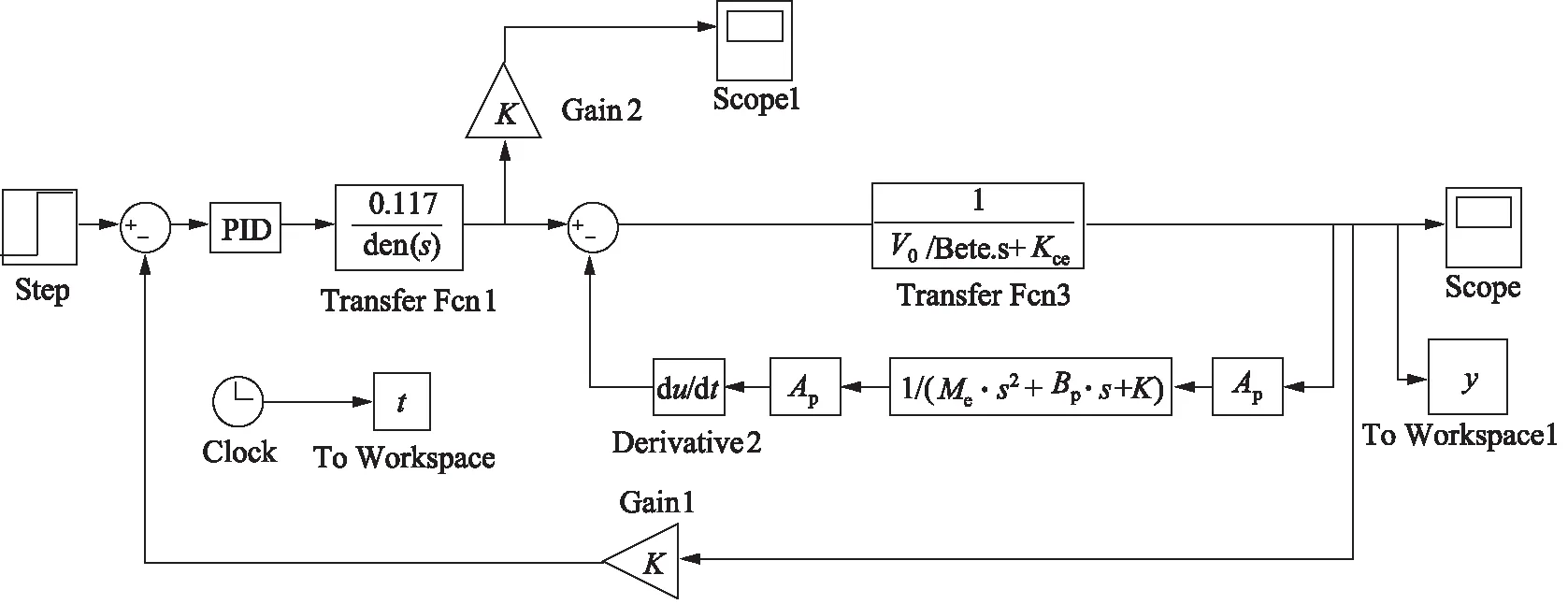
图4 压力控制系统Simulink仿真模型图
式中:mt为活塞及负载等效到活塞上的总质量,kg;xp液压缸活塞位移,m;K为负载弹性刚度,N·m;Bp为活塞及负载黏性阻尼系数,N·s/m。
2.4 压力传感器方程
压力传感器的作用是将液压缸的压力值转化为电信号反馈到控制器,使系统形成压力闭环控制[5]。当传感器频宽足够大时,可以以比例环节来表示传感器的传递函数。可以忽略其动态特性,传递函数可以表示为:
Uf=KfppL
(6)
由式(1)~(6)可知压力控制系统框图,如图3所示。图中Kce=Kc+Ctp。
2.5 参数计算
压力控制系统增压缸的各参数值如表1。
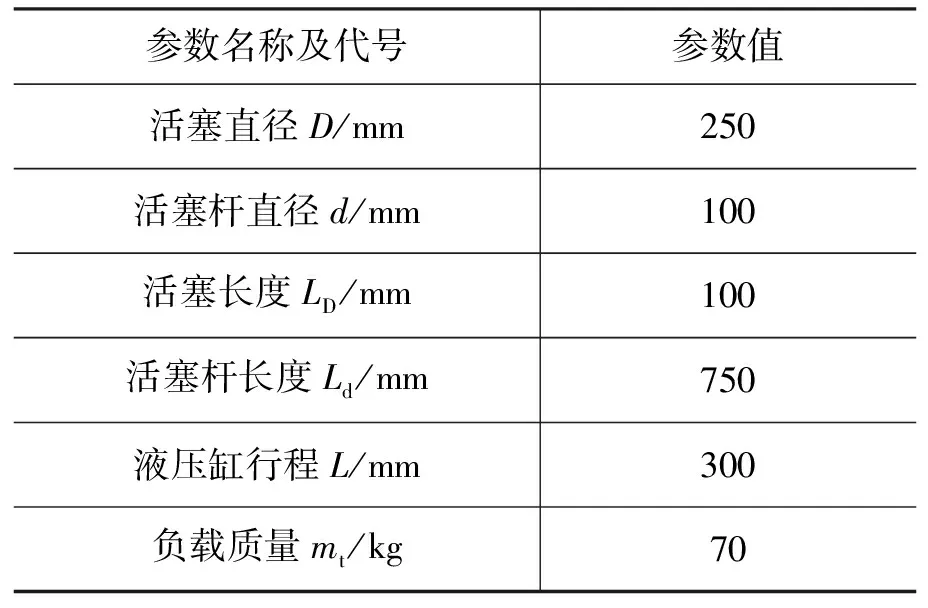
表1 压力控制系统增压缸参数值
由以上参数可得液压缸有效作用面积为:
本系统阀到缸的距离很短,可忽略液压缸两侧的管路容积,因此系统总的压缩容积为:
Vt=ApL=4.12×10-2×0.3=1.24×10-2m3
系统中油液压缩性、液压缸机械柔性及油液中所含的空气量等因素都会影响βe值的大小,因此,要尽量减少系统中混入的空气量。在此选取βe=700 MPa。于是可得:
3 电液压力伺服控制系统的Simulink仿真分析
根据以上分析得到的方框图建立压力控制系统Simulink仿真模型,如图4所示。在仿真模型中,PID控制器的控制参数由试凑法获得:KI=0.01,KP=0.1。
程序运行结束后可以利用Simulink的线性化分析工具对搭建的系统模型进行线性化分析,得到压力控制系统的阶跃响应,如图5所示。根据分析我们可以得出响应时间约为20 ms,有小幅度的超调,满足快速性要求;同时,通过对稳态误差进行分析可知,本控制系统的稳态误差为零,满足稳定性要求。因此可知,控制器基本满足控制要求。
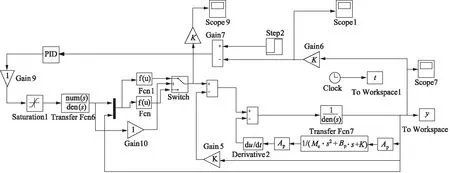
图7 考虑伺服阀的非对称性及饱和的压力系统Simulink模型
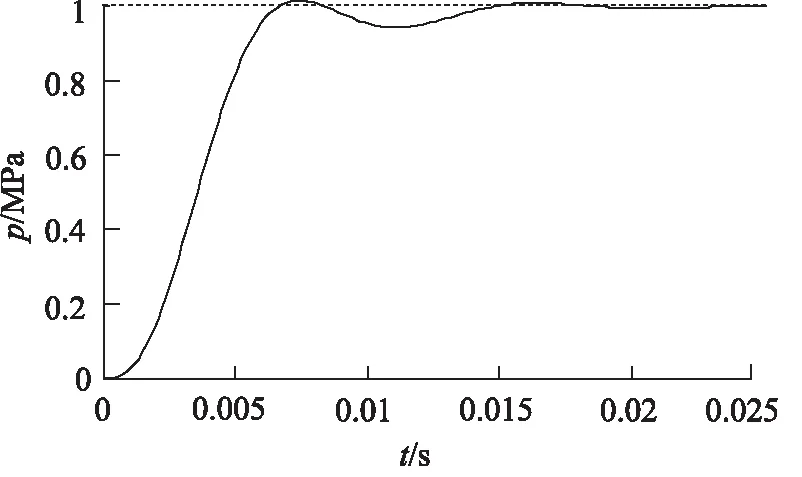
图5 压力控制系统阶跃响应图
同时也可以得到压力控制系统的开环Bode图,如图6所示。对于一个稳定系统来说, 通常要求幅值裕度大于零,相角裕度最好在30°到60°之间。根据获得的本系统的开环伯德图可得到系统的幅值裕度为Gm=9.77 dB,相位裕度为Pm=68.7°,满足上述条件,因此,可以得出,搭建的系统在进行PID调节后处于稳定状态。
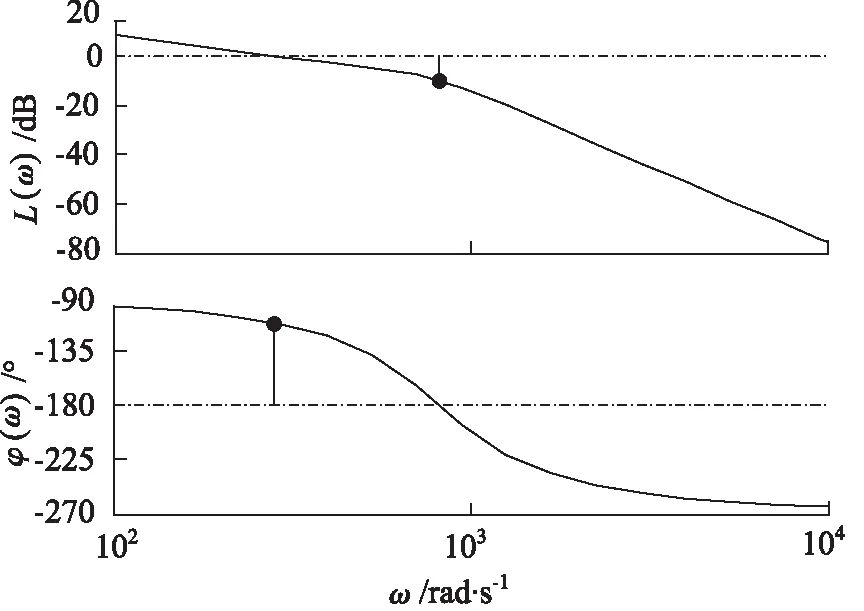
图6 压力控制系统的开环Bode图
在实际应用中,伺服阀具有流量饱和性,即随着输入电流的增加,伺服阀的输出流量不再随之增加,而是呈饱和状态。这就直接影响到液压缸等执行元件的速度和承载能力。同时伺服阀阀芯左移和右移时通过伺服阀的流量也是不同的。
当阀芯左移时,xv>0,通过的流量为:
(7)
式中,ps为供油压力,Pa。
当阀芯右移时,xv<0,通过的流量为:
(8)
针对这些因素,继续完善压力控制系统的Simulink模型,即将伺服阀的流量饱和性及阀芯移动方向不同造成的流量不同等特性考虑进模型的建立。建立了如图7所示的压力控制系统仿真模型。
对图7的模型进行仿真,可得压力控制系统的阶跃响应,响应时间约为35 ms,如图8所示;以及其开环Bode图,如图9所示。由Bode图可知系统的幅值裕度Gm=6.22 dB,相位裕度为Pm=51.7°,可知系统稳定。

图8 考虑伺服阀饱和等因素的压力系统阶跃响应
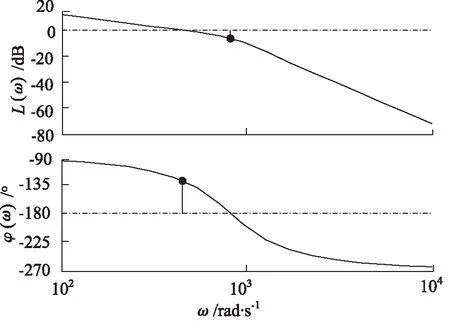
图9 考虑伺服阀饱和等因素的压力系统开环Bode图
4 结论
针对高压润滑拉拔机的实际工作要求设计了压力伺服控制系统,通过基本方程建立了其数学模型,并基于Simulink平台搭建了仿真模型。通过仿真可以验证出此控制系统可以满足工程要求,具有一定的实用价值。
参考文献:
[1] 袁卓林,雷玉勇,孙书蕾,等.基于MATLAB的电液位置伺服系统设计及仿真[J].设计与研究,2009,(5):9-12.
[2] Chiou Y,Lan L.Genetic Fuzzy Logic Controller:an Iterative Evolution Algorithm with New Encoding Method[J]. Fuzzy Sets and System,2005,152(3):617-635.
[3] 孙衍石,靳宝全,熊晓燕,等.电液伺服比例阀控缸位置伺服控制系统AMESim/MATLAB联合仿真研究[J].液压气动与密封,2009,(4):38-42.
[4] 汪桂云,王勇勤,严兴春.液压伺服阀控缸动态特性数学建模与仿真分析[J].四川大学学报,2008,40(5):195-198.
[5] 叶湘滨,等.传感器与测试技术[M].北京:国防工业出版社,2007.

