基于Fluent的某滑阀内部流场仿真与分析

， ，

(兰州理工大学 能源与动力工程学院， 甘肃 兰州 730050)

引言

液压阀是液压系统中非常重要的元件，主要通过控制流体的压力、流量和流动方向来满足工作要求，使各类执行元件实现不同的动作[1]。液压控制阀的内部结构比较复杂，主要由阀体、阀芯、操纵控制机构等主要零部件组成。滑阀类的阀芯是圆柱形，通过阀芯在阀体孔内的滑动来改变液流通路开口的大小，以实现对液流压力、流量及方向的控制。非全周开口滑阀具有水力半径大，抗阻塞的特点，其流量范围大，易得到较小的稳定流量，在液压比例阀和伺服阀中得到了广泛应用[2]，节流槽滑阀的特性分析对液压阀的性能提升起着很重要的作用。

近几年随着计算机科学技术的不断发展以及计算流体力学理论的丰富。人们借助CFD技术对液压阀复杂内部流场进行数值模拟和可视化分析，成为液压领域的热点。在液压技术中，流体仿真主要研究方向有：气穴现象分析，流场速度压力流量分析和液动力分析等。文献[3-6]利用Fluent软件分别对伺服阀、电磁阀、滑阀式换向阀以及液压比例阀的三维扇形区域内部流场进行模拟仿真，得到压力与流量，稳态液动力与阀口开度之间的关系。文献[7]采用CFX软件对三维溢流阀模型的内部流场进行模拟仿真，并结合流体动力学方程对溢流阀的瞬态流场特性和动态特性进行了研究。目前对液压阀内部流场的仿真分析主要是针对全周开口滑阀即传统滑阀,关于节流槽滑阀又称为非全周开口滑阀的研究比较少。本研究以非全周开口液压阀滑阀为研究对象，针对滑阀的内部流场进行三维稳态仿真模拟。采用有限元分析软件ANSYS的前处理模块GAMBIT，分析计算模块Fluent以及后处理模块TECPLOT，得到了滑阀内部流场的速度压力、流量特性以及流量系数随阀口开度的变化规律。

1 计算流体力学基础

任何物体的运动都要遵循一些运动规律，流体运动也不例外，因此滑阀内部流体的流动也要遵循质量守恒定律、动量守恒定律、能量守恒定律。

1.1 流体动力学的连续性方程

连续性方程就是我们所说的质量守恒方程，质量守恒定律是流体力学中最基本的定律。在一定的时间内，某一特定平面上流入的流体质量与流出的相等，得到流体流动时的质量守恒微分方程[8]：

(1)

式中：ux、uy、uz分别为x、y、z，3个方向上的速度分量，m/s；t为时间，s；ρ为流体密度，kg/m3。

1.2 流体动力学的动量方程

(2)

式中：Su,Sv和Sw是动量守恒方程的广义源项，Su=Fu+sx，Sv=Fv+sy，Sw=Fw+sz，其中，sx，sy和sz表达式：

1.3 湍流模型

流体的流动状态可以分为层流和湍流，而湍流在自然界中很常见，大部分工程中的流动问题都是湍流模型[9]。

湍流模型主要有随机性、有涡性、扩散性和耗散性等特征。当流体通过液压阀时，在液压阀内部由于节流口的作用，使流体流动的时候雷诺数很大，因此液压阀内部流场的流动状态是湍流。

2 液压阀阀口流场的分析

2.1 几何模型的建立

液压阀模型的正确建立对后续的仿真计算有着非常重要的意义。为了使模型很好的反应出流场的流动情况，在建模的时候对模型要进行适当的简化。采用三维设计软件对滑阀阀口开度分别为：10 mm、16 mm、22 mm时进行建模，主阀芯直径为120 mm,流道油液进口直径为140 mm，为了能够清楚的看出在不同阀口开度下流场的运动情况，取每个阀口开度下的1/4来进行流场仿真，其中开度为16 mm时的三维模型如图1所示。

图1 开口为16 mm时三维模型

2.2 采用GAMBIT进行网格划分如图2所示

图2 开口为16 mm时网格划分

2.3 边界条件的设置及相关的流体参数

(1) 本研究中所使用的液压滑阀是比较理想的，装配精确并且加工良好，没有什么缝隙和瑕疵；

(2) 所使用的流体不可压缩，是理想流体；

(3) 流体与壁面的接触边界是无滑移壁面；

(4) 采用的边界条件为压力入口和压力出口。操作环境在标准大气压下，其中取进口压力为2.1 MPa， 液压油密度为889 kg/m3，油液动力黏度为0.03556 kg/(m·s)。

3 液压阀内部流场的计算结果

3.1 压力分布云图

在保证其它条件相同的情况下分别对阀口开度为10 mm、16 mm、22 mm时进行流场仿真，压力分布云图如图3～图5所示。

图3 阀口开度10 mm,压差2.1 MPa时压力分布图(Pa)

图4 阀口开度16 mm,压差2.1 MPa时压力分布图(Pa)

图5 阀口开度22 mm,压差2.1 MPa时压力分布图(Pa)

从压力分布图以及压力值可以看出，当流体流经节流槽阀口时，压力下降比较快。随着阀口开度的增大，流场的最低压力减小，阀口开度为16 mm和 22 mm 时流场的最低压力相差不大，但是与10 mm相比，最低压力还是有所降低。压力的变化范围也随着阀口开度的增大而增大。由于流体流经节流槽时流速很高，根据动量守恒定律，该处的压力会很低，甚至有负压会产生，可能会产生气穴现象，当液压系统中有气穴现象产生时，会造成液压系统不稳定。

3.2 速度分布云图

以阀口开度为10 mm、16 mm时的速度分布图为例，如图6，图7所示。

图6 阀口开度10 mm,压差2.1 MPa时速度分布图(m/s)

图7 阀口开度16mm,压力差2.1MPa时速度分布图(m/s)

从上图可以看出，在相同的压差条件下，阀口开度为10 mm和16 mm时，滑阀流场处的最大速度降低,并且随着阀口的增大，阀口处的最大速度也随之降低。流体在进口处的速度基本不变，但在经过阀口时，速度发生急剧变化，经过阀腔时流速产生扩散。在不同压差条件下，对开度为16 mm时的该滑阀进行了内部流场仿真，得到：在相同的开口条件下，随着压差的增大，阀口的流速会随之增大。

4 液压阀压力流量特性分析

4.1 不同阀口开度下的流量特性分析

滑阀的压力流量特性是指流经滑阀的流量与阀口开度以及阀口压差三者之间的关系。由流量公式得到流量系数Cd的公式：

(6)

式中：qν为流量，m3/s；A为阀口过流面积，m2；ρ为液压油密度，kg/m3；Δp为阀口进出口压力差，MPa。

根据仿真结果得到该滑阀在不同开度下的压力-流量特性曲线图，如图8所示。

图8 不同阀口开度下的压力-流量特性曲线

从图中可以看出通过阀口的流量与开度呈线性分布的关系，表明在滑阀开启的过程中流量与阀口开度成正比。

通过式(6)我们得到不同阀口开度下的压力-流量系数曲线，如图9所示。

从图9可以看出：节流槽阀口的流量系数与阀口的开度大小密切相关的。随着阀口开度的减小，流量系数逐渐增大。

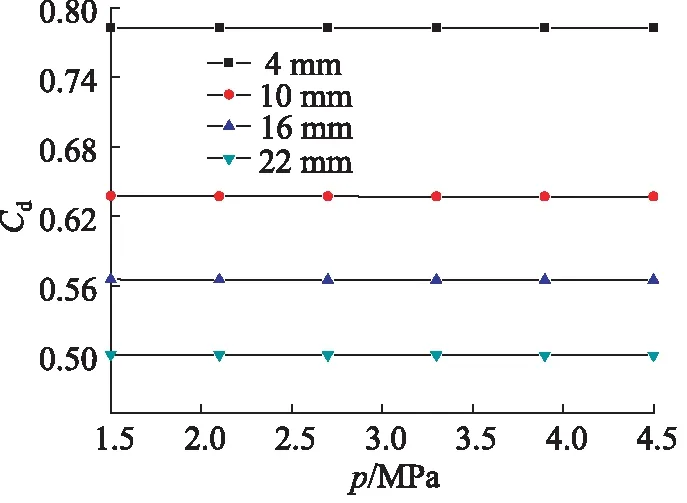
图9 不同阀口开度下的压力-流量系数曲线

4.2 与半圆形槽滑阀的比较

半圆形槽示意图如图10所示。

图10 不同节流槽形状下的压力-流量系数曲线图

在相同条件下，对阀口开度为16 mm的半圆形槽滑阀进行模拟仿真，将得到的数据代入式(6)中得到流量系数值，并且与之前的矩形节流槽比较，结果如图11所示。从图中看出：滑阀流量系数与节流槽的形状有关；在阀口开度相同的条件下，半圆形槽滑阀与矩形节流槽滑阀相比较，流量系数变化较平缓，并且随着进出口压差的增大都有缓慢下降趋于稳定的趋势。

图11 半圆形槽示意图

5 结论

本研究对液压阀滑阀进行了内部流场的仿真分析，得出如下结论：

(1) 在进出口压差相同的条件下，流体流经节流槽阀口时，压力下降较快；随着阀口开度从10 mm增加到6 mm时，流场的最低压力有所增加，阀口开度为16 mm 和22 mm时流场的最低压力相差不大，但是与10 mm相比，最低压力有所下降.压力的变化范围也随着阀口开度的增大而增大。

(2) 进出口压差相同的情况下，随着阀口开度的增大，阀口的最大速度随之降低；在相同的开口条件下，随着进出口压差的增大，阀口的流速会随之增大；流体在进口处的速度基本相同，但在经过阀口时，速度发生急剧变化，经过阀腔时流速产生扩散。

(3) 滑阀节流槽阀口的流量系数与阀口的开度大小，进出口压力差以及节流槽形状紧密相关。在相同压差条件下，随着阀口开度的减小，流量系数逐渐增大；在相同的阀口开度下，随着进出口压差的增大，流量系数在逐渐减小，半圆形槽滑阀与矩形节流槽滑阀相比较，流量系数变化较平缓，并且，随着进出口压差的增大都有缓慢下降趋于稳定的趋势。

参考文献：

[1] 李壮云.液压元件与系统(第三版)[M]. 北京：机械工业出版社，2011.

[2] 冀宏，张继环，王东升，等.滑阀矩形节流槽阀口的流量系数[J].兰州理工大学学报，2010，36(3)：1-2.

[3] 吕庭英，黄效国，何康宁.基于Fluent的液压伺服阀液动力研究[J].机床与液压，2011,39(13)：131-132.

[4] GEE Soo Lee， HYUNG Jin Sung， HYUN Chul Kim, et al. Flow Force Analysis of a Variable Force Solenoid Valve for Automatic Transmissions[J]. Journal of Fluids Engineering，2010，132(3)：782-793.

[5] 周元春，杨曙东，王金林，等. 基于Fluent的大通径滑阀压力流量特性研究[J].机床与液压，2011，39(19)：103-105.

[6] Jose R.Valdes，Mario J. Miana，Jose L. Nunez, et al. Reduced Order Model for Estimation of Fluid and Flow Forces in Hydraulic Proportional Valves [J]. Energy Conversion and Management，2008，49(8)：1517-1529.

[7] XUE Guan Song，LIN Wang， YONG Chul Park. Transient Analysis of a Spring-Loaded Pressure Safety Valve Using Computational Fluid Dynamics(CFD)[J]. Journal of Pressure Vessel Technology，2010，132(5)：156-164.

[8] 金晓宏，李远慧.流体力学[M].北京：中国电力出版社，2011.

[9] 潘永成，王勇，等.基于CFD的调节阀内流场流动特性研究[J].机床与液压，2011，(1)：5-7.