基于OpenSees的RPC桥墩拟静力数值模拟与参数分析

任 亮，方 志，王 诚

(1.湖南大学 土木工程学院，湖南 长沙 410082；2.华东交通大学 土建学院，江西 南昌 330013)

作为一种新型建筑材料，活性粉末混凝土(简称RPC)具有抗压强度高、韧性良好和耐久性能优异等优点。由于混合料全部采用细骨料，RPC在长期荷载作用下徐变较小，而特殊的养护环境(热养护)使RPC几乎没有收缩[1，2]，因此适合做大跨度桥梁的桥墩结构。但目前国内外对RPC材料在桥梁工程中的应用研究还较少，尤其是构件抗震性能方面研究还比较薄弱，已有研究主要集中在无轴力和常轴力作用下RPC构件拟静力试验研究[3，4]。在地震荷载作用下，桥梁墩柱通常是受力最敏感也是最易破坏的结构构件，其滞回耗能特性在一定程度上决定了桥梁的整体抗震能力。因此，基于有限的拟静力试验结果较可靠模拟RPC构件在反复荷载作用下的非线性滞回特性具有重要意义。

OpenSees全称Open System for Earthquake Engineering Simulation，是由美国太平洋地震工程研究中心、加州大学伯克利分校等共同开发并用于岩土和结构方面地震模拟的开放式系统。该系统具有丰富的材料和单元类型，包含大量求解算法，其源代码的开放性使系统更易于改进和协同开发，目前已引起国内外研究人员的关注和重视[4-7]。但RPC作为一种新型超高性能混凝土，在OpenSees材料库中目前尚无材料本构关系。为应用OpenSees既有材料本构关系模拟RPC材料，本文以3个常轴力作用下的大比例RPC桥墩水平反复加载滞回试验结果为依据，通过选取OpenSees中适当的材料本构关系和单元类型对RPC桥墩的滞回特性进行数值模拟，并在此基础上运用OpenSees分析轴压比、纵筋率和水平荷载加载方向等参数对RPC桥墩延性抗震性能的影响。

1 RPC桥墩拟静力试验

1.1 试验概述

为探讨RPC桥墩在地震作用下的抗震性能，对3个常轴力作用下的RPC桥墩试件施加低周水平反复荷载，研究加载方向对RPC桥墩抗震性能的影响。图1为试件截面尺寸和配筋情况，其中纵筋和箍筋分别采用HRB400和HRB335热轧钢筋。表1为试件各参数值。

图1 试件截面尺寸和配筋(单位：mm)

试验加载装置如图2所示。水平力加载通过最大水平力为500 kN、最大水平位移为600 mm的水平作动器施加；竖向力通过放置在试件顶部加载横梁上的两个中空液压千斤顶对称张拉竖向高强钢棒来施加，加载极值为2 000 kN。考虑到拟静力试验加载过程中高强钢棒在轴向力作用下自身可能产生弯曲，导致桥墩试件偏心受压，为消除其影响，在高强钢棒底部设计一个可以自由转动的单向铰来保证加载过程中高强钢棒和横梁随墩帽同时转动。试验加载采用位移循环控制方式，相应加载制度如图3所示。

表1 试件参数

注：试件编号中R代表RPC，P代表桥墩(Pier)，数字代表截面长边与加载方向之间的夹角(°)。

图2 试验加载装置图(单位：mm)

图3 加载制度示意图

1.2 试件破坏形态

RPC桥墩试件在拟静力荷载作用下首先在根部出现局部水平微裂缝，随着水平力的持续增加，RPC桥墩试件根部不断出现新的微裂缝，而根部原有裂缝的长度和宽度也迅速发展，并逐渐贯通形成肉眼可见的斜向裂缝；与此同时，在RPC桥墩试件根部开裂处可以明显观察到钢纤维相继被拉断，部分甚至被拔出。最终破坏时RPC桥墩试件根部混凝土被压碎并脱落，根部裸露的纵筋出现明显屈服，其中对角轴加载的RPC桥墩试件R-P-34还出现部分纵筋被拉断的现象。图4为3个试件最终破坏形态。

(a)R-P-0

(b)R-P-34

(c)R-P-90图4 试件破坏现象

1.3 骨架曲线

图5为3个RPC桥墩试件在低周水平反复荷载作用下的骨架曲线对比，从图5可以看出：

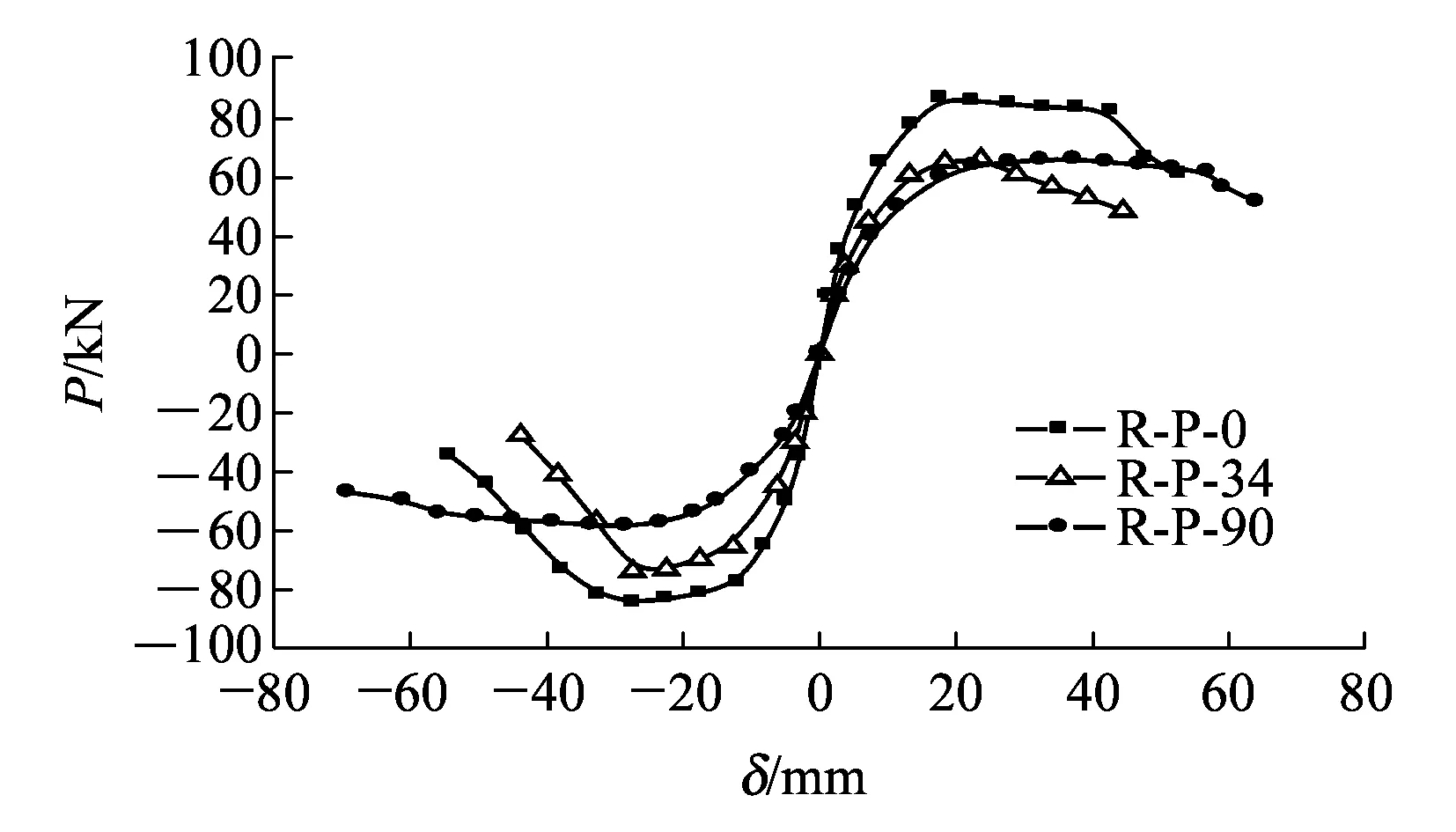
图5 试件骨架曲线对比

(1)RPC桥墩试件在不同的水平荷载加载方向时，骨架曲线均表现出较明显上升段、强化段和下降段；

(2)主轴加载试件R-P-0和试件R-P-90骨架曲线经过极值点荷载后均出现明显的强度下降平台，说明其在反复荷载作用下具有较好的延性；对角轴加载试件R-P-34骨架曲线经过极值点荷载后有快速下降的趋势，延性较其余两试件差，说明水平荷载加载方向对RPC桥墩试件延性抗震性能有较大影响。

2 材料本构关系及其拟合

2.1 RPC本构关系

考虑到目前有约束RPC材料应力-应变关系无相关文献，为此选用无约束RPC材料应力-应变关系，相应的受压本构表达式为[8]

( 1 )

式中：ε和σc分别表示压应变和压应力；ε0和εu分别表示峰值点应变和极值点应变，其值分别取3 500×10-6和4 500×10-6；fc为棱柱体抗压强度；ξ=ε/ε0；n=E0/Es，其中E0表示初始弹性模量，Es表示峰值点割线模量。E0可由式( 2 )计算求得。

( 2 )

RPC受拉应力-应变关系考虑钢纤维的抗裂效应，其表达式为[9]

( 3 )

式中：εt为拉应变；σt为εt对应拉应力；εt0为峰值点对应拉应变；εtu为极限拉应变，且εtu=2εt0；ft为极限抗拉强度，其值为RPC立方体抗压强度的1/23.6；Ec为抗拉弹性模量，其值与初始弹性模量E0一致。

2.2 RPC本构关系在OpenSees中的拟合

考虑到OpenSees系统中Concrete02材料(采用Scott、Park等人修正的Kent-Park混凝土本构模型)能较好模拟混凝土压弯构件在反复荷载作用下的滞回特性，本文选用Concrete02本构关系对RPC本构关系进行拟合，相应的应力-应变滞回关系如图6所示。

图6 Concrete 02应力-应变滞回关系

不考虑箍筋约束时，受压骨架曲线为

( 4 )

其中

( 5 )

式中：Zm为骨架曲线下降段对应斜率；εc为压应变；σc为εc对应压应力；fc为混凝土棱柱体抗压强度；ε0为峰值点压应变；εu为极限压应变；sh和h′分别表示箍筋间距和从箍筋外边缘算起的核心混凝土宽度；ρs为体积配箍率。

考虑到Concrete02中Zm为输入项，因此在OpenSees中可通过调整Zm值拟合RPC材料应力-应变关系，其中Zm取值必须保证峰值点压应变和极限压应变间RPC应力-应变曲线和拟合曲线相关度不低于95%，相关系数可通过Excel中的相关函数CORREL确定。

受拉骨架曲线为

( 6 )

式中：σt为拉应力；εt为拉应变；εt0为峰值点拉应变；Ec为骨架曲线受拉初始弹性模量；Ets为骨架曲线受拉软化段曲率；ft为混凝土极限抗拉强度。

现取ε0=0.003 5，εu=0.004 5，εt0=1.34×10-4，εtu=2.68×10-4，fc=140 MPa，ft=6 MPa，Ec=Ets=44.8 GPa，通过调整Zm值得到如图7所示RPC材料本构与Concrete02拟合本构对比。

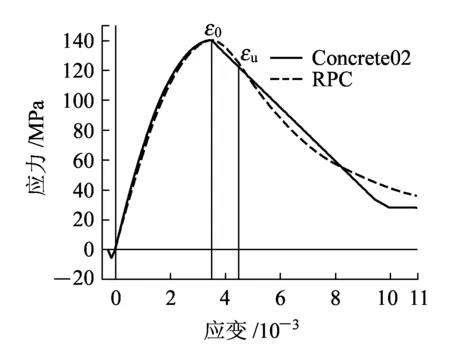
图7 RPC材料与Concrete02拟合本构对比

注：图中应力拉为负，压为正；应变拉为负，压为正。

从图7可以看出，Concrete02与RPC受压骨架曲线上升段能较好吻合，下降段在极限压应变之前两者基本吻合；受拉骨架曲线在上升段两者吻合较好，下降段Concrete02材料为直线下降，而RPC材料在经过峰值点拉应变后为水平直线，但考虑到RPC材料以受压为主，因此与Concrete02受拉骨架曲线对比，下降段存在的偏差可以接受。

2.3 钢筋本构关系

考虑到试件在低周水平反复加载后期出现明显的强度和刚度退化、试件根部纵筋出现屈服甚至拉断的现象，选用OpenSees中的Steel02材料[10]对RPC桥墩非线性滞回特性进行模拟，相应的应力-应变滞回关系如图8所示。

图8 Steel02应力-应变滞回关系

Steel02采用Menegotto-Pinto钢筋模型，相应的模型表达形式为

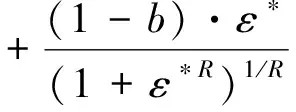
( 7 )

其中

( 8 )

( 9 )

(10)

式中：ε0和εr分别表示钢筋的屈服应变和双线性包络线反向点处钢筋应变；σ0和σr分别表示钢筋的屈服应力和双线性包络线反向点处钢筋应力；a1和a2为材料常数；b=E1/E0，其中E0为钢筋初始弹性模量，E1为钢筋硬化模量；ξ为上一级循环对应的塑性应变绝对值；R0为考虑包辛格效应的钢筋常数。

3 考虑墩底纵筋滑移的滞回分析模型

基于上述拟合的RPC本构关系和Steel02钢筋本构关系，应用非线性梁柱单元模拟RPC桥墩试件的非线性行为，应用零长度单元模拟RPC桥墩试件根部钢筋与活性粉末混凝土间的黏结-滑移效应，本文建立考虑墩底纵筋滑移的滞回分析模型，如图9所示。

图9 考虑墩底纵筋滑移的滞回分析模型

图9中非线性梁柱单元和零长度单元均采用截面纤维模型，为准确描述构件沿高度方向柔度的变化，首先将构件沿高度方向设置多个以力插值函数为基础的积分控制点，然后根据钢筋和混凝土应力-应变关系迭代求得各纤维单元的刚度和抗力，最后通过Gauss-Lobatto积分计算出截面所有单元的刚度矩阵和抗力矩阵。零长度单元采用同一个位置的2个节点(图9中的节点i和节点j)来表示，节点对应的截面与非线性梁柱单元截面具有相同的混凝土和钢筋配置，且混凝土和钢筋的纤维划分一致；不同之处在于非线性梁柱单元截面钢筋纤维的本构关系为前述Steel02应力-应变关系，零长度单元截面钢筋纤维的本构关系为钢筋的应力-滑移(σ-s)关系。由于目前尚无钢筋在活性粉末混凝土中的应力-滑移关系文献，本文参考文献[11]中钢筋应力-滑移关系和定参方法，其中的滑移量s(如钢筋屈服时对应的滑移)根据UEDA[12]等完成的梁柱内部钢筋锚固性能试验数据经回归分析求得，滞回规则根据LIN[13]完成的具有足够锚固长度的钢筋反复加载滑移规律来确定，如图9所示。其中的应力-滑移骨架曲线假定关于原点对称，且反复加载过程中，卸载刚度按初始刚度取值，加载路径由以下各式确定

σ=σ*·σmaxσ>0

(11)

σ=σ*·σminσ<0

(12)

(13)

(14)

(15)

(16)

4 RPC桥墩拟静力数值模拟

基于考虑墩底纵筋滑移的滞回分析模型，本文对3个RPC桥墩试件在常轴力作用下的低周水平反复荷载试验进行数值模拟，图10和图11分别为试件骨架曲线和滞回曲线试验值与计算值对比。

(a)R-P-0

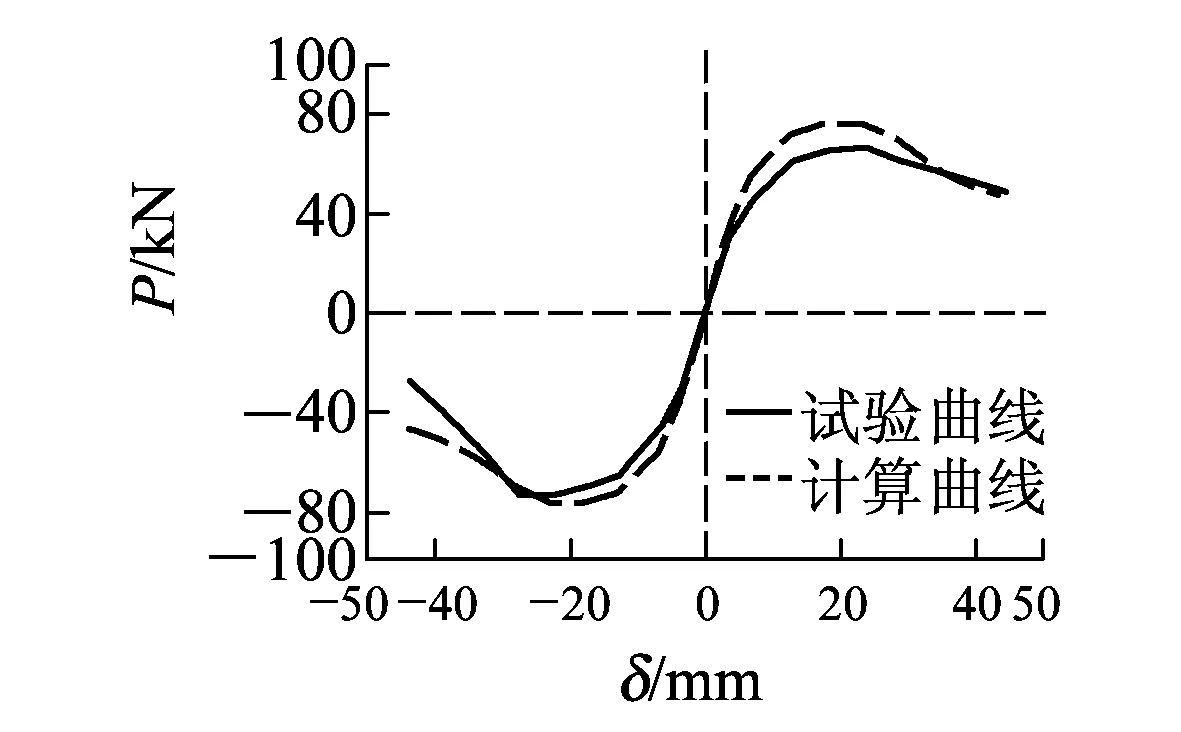
(b)R-P-34

(c)R-P-90图10 骨架曲线对比

(a)R-P-0试验曲线

(b)R-P-34试验曲线

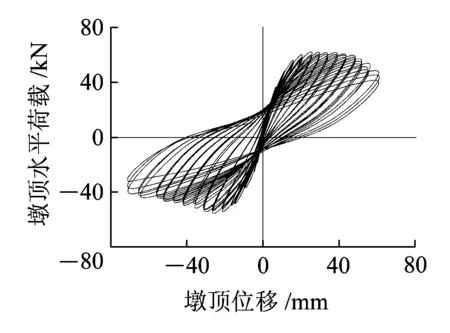
(c)R-P-90试验曲线

(d)R-P-0计算曲线

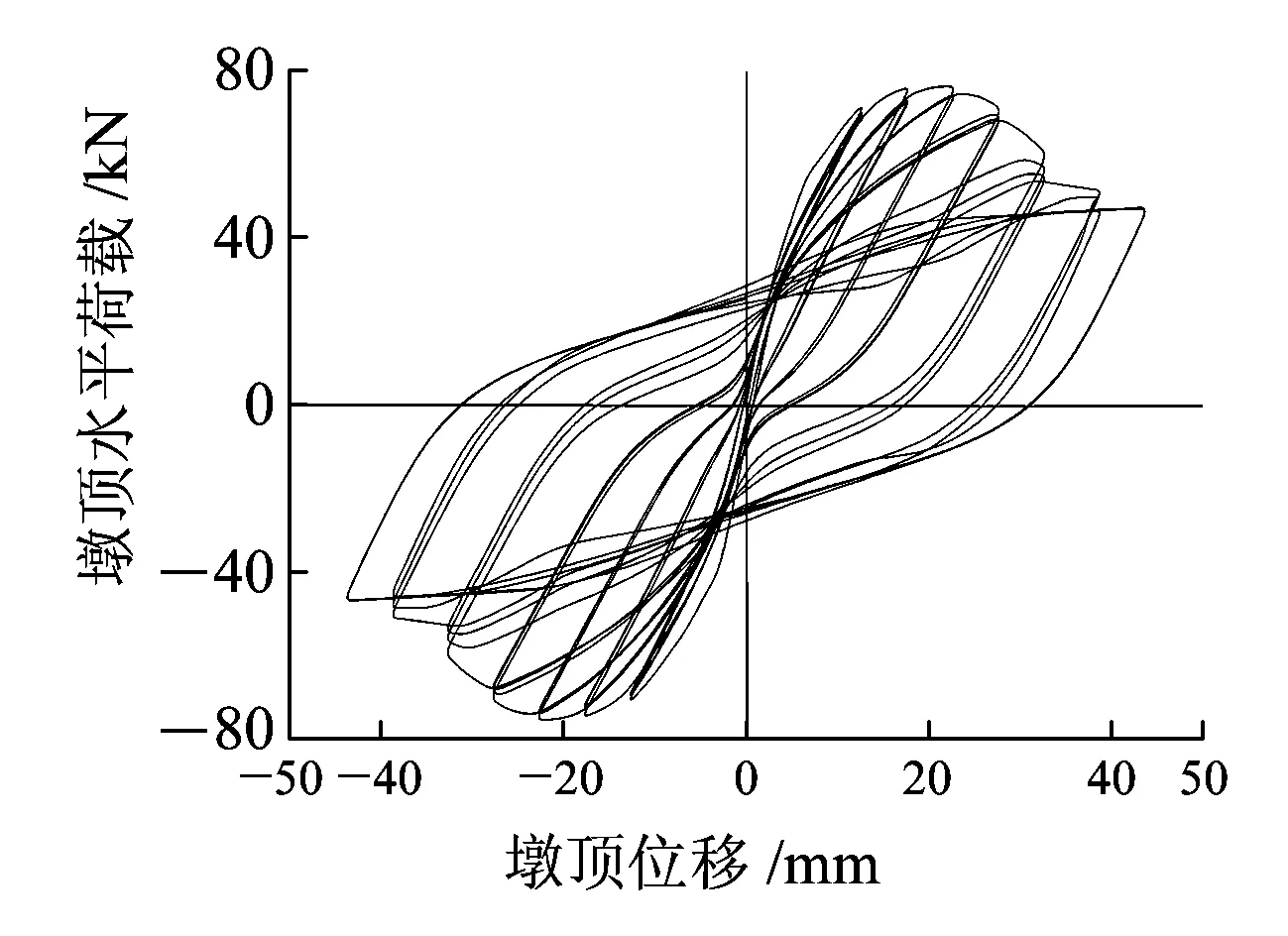
(e)R-P-34计算曲线

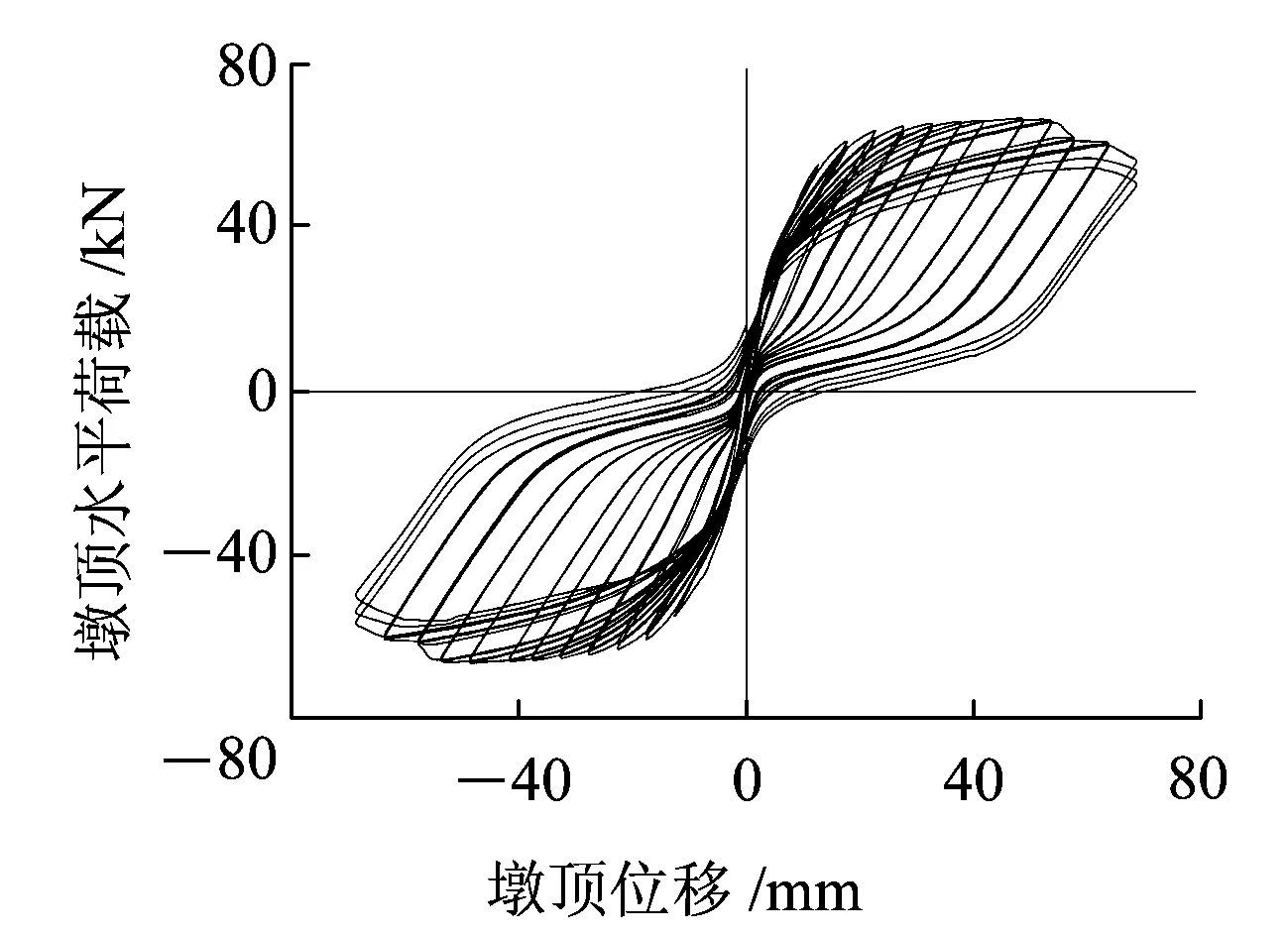
(f)R-P-90计算曲线图11 滞回曲线对比

从图10可以看出，2组曲线形状相似但试验曲线峰值点荷载偏小，这是由于RPC桥墩试件在反复荷载作用下已产生损伤，在一定程度上降低了结构承载力；2组曲线开裂前吻合较好，开裂后存在偏差，其中试件R-P-34由于未考虑扭转变形影响偏差最大。

从图11可以看出，3个RPC桥墩试件在水平反复荷载作用下的滞回曲线上升段和强度退化均得到较好模拟，但经过峰值点荷载后试件均出现不同程度的快速卸载现象，这是由于Concrete02本构下降段为线性下降；由于数值模拟未考虑扭转变形的影响，试件R-P-34模拟效果较试件R-P-0和试件R-P-90差。

因此，综合考虑计算值与试验值的差异性后，本文应用OpenSees中的Concrete02本构关系和Steel02本构关系，结合非线性梁柱单元和零长度单元能较好模拟RPC桥墩的骨架曲线和滞回曲线，并能反映试件在反复加载过程中强度和刚度的退化。

5 参数分析

为进一步探讨RPC桥墩在拟静力荷载作用下的延性抗震性能，本文应用上述方法分析轴压比、纵筋率和水平荷载加载方向等参数对RPC桥墩位移延性系数(极限位移与屈服位移比值)的影响。分析时试件高度、截面尺寸与原RPC桥墩相同，为方便表述，将加载角0°方向称为截面强轴，加载角90°方向称为截面弱轴。

5.1 轴压比

轴压比是影响桥墩延性的重要因素之一。图12是纵筋率分别为1.9%、2.7%和3.7%时位移延性系数随轴压比变化的曲线(加载方向按强轴考虑)。

图12 位移延性系数随轴压比的变化

从图12可以看出，在轴压比小于0.2时，位移延性系数随轴压比的增大下降较快；当轴压比大于0.2时，位移延性系数随轴压比的增加缓慢降低，并逐渐接近1。这说明轴压比增加到一定程度，RPC构件将表现出明显的脆性。

5.2 纵筋率

纵筋率是影响桥墩延性的另一重要因素。图13是轴压比分别为0、0.1、0.2和0.3时位移延性系数随纵筋率变化的曲线(加载方向按强轴考虑)。

图13 位移延性系数随纵筋率的变化

从图13可以看出，当轴压比小于0.2时，位移延性系数随纵筋率的提高降低明显，这是由于轴压比较小时，桥墩发生适筋破坏，虽然墩的屈服位移或屈服曲率随纵筋率提高而增加，但墩的极限位移变化较小，降低了墩的延性；当轴压比大于0.2时，RPC构件表现出明显的脆性，位移延性系数随纵筋率的提高无明显改变。

5.3 水平荷载加载方向

从前述拟静力试验结果可以看出，水平加载角对RPC桥墩延性影响较大，为此选取0°、15°、30°、45°、60°、75°和90°水平加载角(对角轴位置和可能的不利加载位置)进行分析。图14分别为不同轴压比和纵筋率时位移延性系数随水平荷载加载方向变化的曲线。

(a)不同的轴压比(纵筋率2.7%)

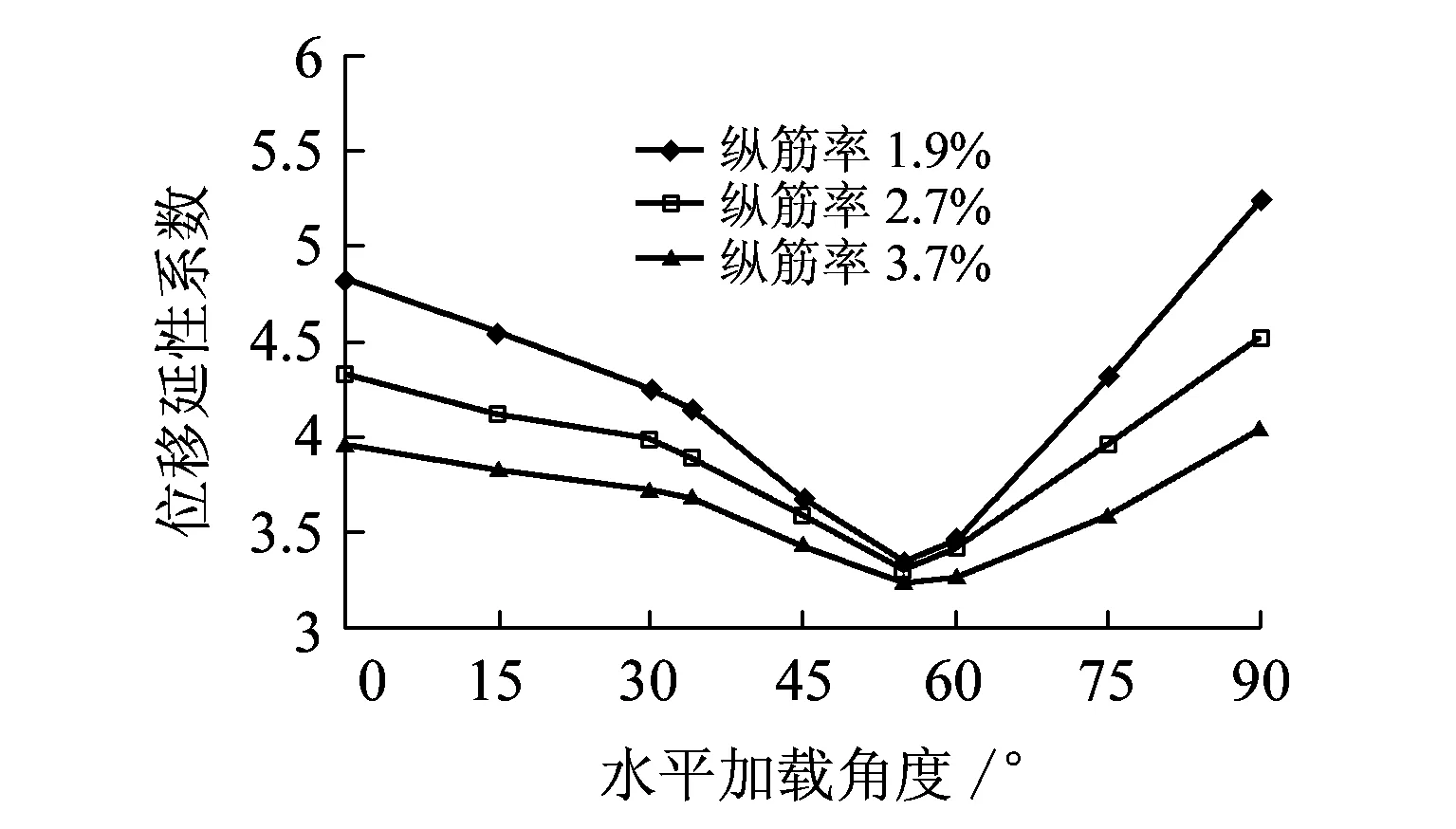
(b)不同的纵筋率(轴压比0.15)图14 位移延性系数随水平加载方向的变化

从图14可以看出，RPC桥墩位移延性系数随水平加载方向的变化而改变，且在主轴(强轴和弱轴)之间存在一个最不利的加载方向角(约为55°)，该加载方向不随轴压比和纵筋率的变化而改变，大致与对角轴垂直。这是由于在该加载方向纵筋之间受力不均匀性最大，导致靠近墩角的受力纵筋在荷载作用下最易屈服，且在屈服后钢筋迅速进入强化阶段并最终被拉断，试件表现出明显的脆性破坏特征，因而延性最低。

6 结论

本文基于OpenSees中既有材料本构关系和单元类型对RPC桥墩进行拟静力数值模拟和参数分析，得到以下结论：

(1)基于适当的参数选取，运用OpenSees中Concrete02本构关系能较好拟合RPC本构关系。

(2)应用OpenSees中既有本构关系和单元类型建立的考虑墩底纵筋滑移的滞回分析模型能较好模拟RPC箱型桥墩的骨架曲线及滞回曲线，并能反映构件在反复加载过程中强度和刚度的退化。

(3)桥墩的位移延性系数随轴压比的增加和纵筋率的提高而降低，随水平加载方向的变化而改变，且在主轴之外存在一个最不利加载方向，该方向不随轴压比和纵筋率的变化而改变，大致与对角轴垂直。

参考文献：

[1]RICHARD P,CHEYREZY M.Composition of Reactive Powder Concrete[J].Cement and Concrete Research,1995,25(7):1501-1511.

[2]BONNEAU O,LACHEMI M.Mechanical Properties and Durability of Two Industrial Reactive Powder Concrete[J].ACI Material Journal,1997,94(4):286-290.

[3]郝文秀,钟铁毅,赵冠远.活性粉末混凝土空心桥墩恢复力模型试验研究[J].铁道学报,2011,33(8):89-93.

HAO Wen-xiu,ZHONG Tie-yi,ZHAO Guan-yuan.Experimental Study on the Restoring Force Model of Reactive Powder Concrete Hollow Piers[J].Journal of the China Railway Society,2011,33(8):89-93.

[4]王诚.活性粉末混凝土箱型桥墩抗震性能试验研究[D].长沙：湖南大学，2010:48-50.

[5]王瑾,蔡新江,田石柱.基于OpenSees的CFRP加固RC短柱抗震性能数值模拟[J].世界地震工程,2009,25(4):108-111.

WANG Jin,CAI Xin-jiang,TIAN Shi-zhu.Numerical Simulation on Seismic Behavior of CFRP Retrofitted RC Short Column Based on OpenSees[J].World Earthquake Engineering,2009,25(4):108-111.

[6]朱雁茹,郭子雄.基于OpenSees的SRC柱低周往复加载数值模拟[J].广西大学学报：自然科学版,2010,35(4):555-559.

ZHU Yan-ru,GUO Zi-xiong.Numerical Simulation of SRC Column under Low Cyclic Loading Based on OpenSees[J].Journal of Guangxi University:Nature Science,2010,35(4):555-559.

[7]李贵乾,郑罡,高波.基于OpenSees的钢筋混凝土桥墩拟静力试验数值分析[J].世界地震工程,2011,27(1):110-114.

LI Gui-qian，ZHENG Gang，GAO Bo.Numerical Analysis for Pseudo-static Tests of Reinforced Concrete Bridge Columns Based on OpenSees[J].World Earthquake Engineering,2011,27(1):110-114.

[8]单波.活性粉末混凝土基本力学性能的试验与研究[D].长沙：湖南大学，2002:35-50.

[9]原海燕,安明喆, 贾方方,等.活性粉末混凝土轴拉性能试验研究[J].工程力学(S1),2011,28(1):141-144.

YUAN Hai-yan,AN Ming-zhe,JIA Fang-fang,et al.Experimental Research on Uniaxial Tensile Performance of Reactive Powder Concrete[J].Engineering Mechanics(S1),2011,28(1):141-144.

[10]MAZZONI S,MCKENNA F,SCOTT M H,et al.OpenSees Command Language Manual[Z].Berkeley:PEER,University of California,2007.

[11]ZHAO J,SRITHARAN S.Modeling of Strain Penetration Effects in Fiber-based Analysis of Reinforced Concrete Structures[J].ACI Structural Journal,2007,104(2):133-141.

[12]UEDA T,LIN I,HAWKINS N M,et al.Beam Bar Anchorage in Exterior Column-beam Connections[J].ACI Structural Journal,1986,83(3):412-422.

[13]LIN I.Anchorage Characteristics for Reinforcing Bars Subjected to Reversed Cyclic Loading[D].Seattle:University of Washington,1981.