高速铁路接触网关键零件的疲劳载荷谱编制

戚广枫，陈建芳，肖晓晖，宋云超

(武汉大学 动力与机械学院，湖北 武汉 430072)

高速铁路是国民经济发展的重要支撑。接触网，作为直接向电力机车供电的线路，是高速铁路的主要组成部分。由于接触网沿铁路露天架设，无备用线路，长期承受自然环境中风载荷等随机载荷和列车行驶过程中的动载荷，疲劳是其主要失效形式之一。因此，研究接触网的疲劳可靠性对保障高速铁路运行安全有重要意义。

针对接触网的疲劳与可靠性分析，文献[1]分析确定了影响接触线疲劳的参数，并采用数值软件(简称OSCAR)评估接触线的载荷，进行疲劳估算。文献[2]提出用扩展有限元理论来预测接触线疲劳裂纹的扩展路线与速率。文献[3]采用故障树模型与最小割集算法评估接触网系统的可靠性指标。文献[4]通过对反定位支持架腕臂进行静、动力学分析，采用模糊数学方法进行腕臂等结构的模糊可靠度分析。文献[5]通过样条插值和极大似然等方法估算分布参数，以应力-强度的干涉模型得到各零部件可靠度。针对接触网的疲劳分析，文献[6]基于接触网支持架的动力学仿真，得到不同频率下的最大应力幅值，根据零件S-N曲线计算零件疲劳寿命。文献[7，8]采用有限寿命设计法，取应力谱的最大值和最小值，对列车低速180 km/h行驶工况下柔性悬挂接触网进行疲劳分析。

综上，针对接触网的疲劳，国内外有不少成果，但针对高速铁路接触网的运行环境与参数，尚缺乏系统地建模与分析。因此，本文针对列车250～300 km/h时速工况，结合接触网故障树模型与有限元动态响应分析得到接触网系统的关键零部件；基于疲劳可靠性设计的理论与方法，编制了关键零件的疲劳载荷谱，为接触网疲劳寿命、可靠性分析奠定基础。

1 高速铁路接触网的结构与受力特点

1.1 高速铁路接触网的结构

接触网主要由接触悬挂、定位装置、支持装置、支柱和基础4部分组成。本文研究的重点是定位装置和支持装置。支持装置主要由腕臂底座、平腕臂、斜腕臂、腕臂支撑、承力索座、定位管等组成；定位装置主要由定位线夹、定位器、定位支座、定位管连接器、定位管支撑、防风拉线等组成。

1.2 接触网的受力特点

高速运行条件下的受流质量，是高速电气化铁路的关键技术之一。列车高速运行时保持稳定的受流状态，即受电弓与接触线间保持一定的接触压力。当接触压力过小，易造成离线，即受电弓脱离接触线或产生电弧；当接触压力过大，接触线抬升量过大，使接触线局部弯曲，引起接触线疲劳损伤，加剧接触线磨耗，严重时造成弓网事故[9]。

本文重点研究接触网零部件在列车高速运行过程中的疲劳可靠性。

2 研究方法

通过对接触网系统故障树模型与有限元动态响应分析，确认接触网系统的关键零部件，对列车行驶典型工况下接触网零部件的应力-时间历程数据进行浓缩，采用雨流法计数，编制接触网定位装置、支持结构的载荷谱。

2.1 接触网关键零部件的确定

本文采用故障树法分析影响接触网结构可靠性的关键环节。建立接触网系统故障树模型，确认接触网系统故障树的全部最小割集，利用串并联可修复系统可靠性指标的计算公式，得到接触网系统的可靠性指标，分析接触网系统中的薄弱环节；提取接触网系统仿真环境下的各部件的应力时程，得到零部件的最大应力值Smax、应力均值Sm、应力幅值Sa。Goodman直线表达式为

(Sa/S-1)+(Sm/Su)=1

( 1 )

式中：S-1为对称循环载荷下材料的疲劳极限；Su为材料的强度极限。若要将一个应力幅值为Sa1、应力均值不为零(Sm1≠0)的应力水平，转换为应力均值等于零(Sm2=0)的应力水平，利用式( 1 )有

(Sa1/Sa2)+(Sm1/Su)=1

( 2 )

可求得Sa2，依据其值的大小对接触网零部件进行重要度排序，最终确定直接影响接触网系统运行可靠性的关键零部件。

2.2 载荷历程的获取

建立接触网的连续多跨有限元模型[10]，腕臂结构简化为一个以梁单元、管单元和杆单元构成的有限元模型。其中，腕臂底座与支柱固接，用梁单元模拟；绝缘子、腕臂以及定位管等部件，根据结构特点和受力情况，用管单元模拟；定位支撑由于两端铰接，只受轴向拉压力，用杆单元模拟。接触网中的承力索、接触线和吊弦选用Link10单元模拟。

对腕臂结构进行列车行驶工况下的动态响应仿真。根据国内现行高铁、动车的行驶工况，确定12种运行工况，即在单弓、双弓两种运行模式250 km/h、260 km/h、270 km/h、280 km/h、290 km/h、300 km/h六种时速。采用完全法进行典型工况下的接触网的动态响应分析，通过仿真结果与现场试验数据的对比分析，验证模型的有效性；提取关键零部件对应的模型节点的力-时间历程，做为关键零件的载荷历程。

2.3 载荷计数

在编制载荷谱时，忽略零件所承受的小载荷段，进行载荷“浓缩”，即截取列车驶至支持架悬挂点前2 s与驶离后载荷幅值衰减至最大振幅10%～20%的时间段为分析的源数据。

结合列车行驶工况下测点载荷-时间历程的幅值与均值，针对不同零件采取不同的载荷级数。在载荷“浓缩”及载荷分级的基础上采用雨流计数法进行计数，得到各关键零部件的应力统计谱。

2.4 编制载荷谱

材料的循环疲劳特性是标准构件在试验条件下获得的，试验条件下施加的载荷通常为零均值等幅交变载荷，而实际工况下接触网系统各零部件的工作载荷也是典型的非零均值等幅交变载荷。应力时间历程经循环计数处理之后得到的输出数据文件是整个历程中各次应力循环的均值和幅值，不仅数据量大，而且具有一定的随机性，不能用于疲劳试验机加载。因此本文采用Goodman直线方法，得到零均值载荷，形成可以用于试验加载的块状程序谱，用于寿命估算和疲劳试验。

3 结果与分析

3.1 关键零件的确定

高速铁路接触网失效的故障树模型如图1所示。定位装置、支持装置故障树见文献[11]。根据接触网系统故障树分析得到接触悬挂、支持装置、定位装置、支柱与基础4部分的最小割集[11]。

图1 接触网故障树模型

接触悬挂故障树的最小割集：承力索，接触线，吊弦，线夹；支持装置故障树的最小割集：斜腕臂，水平腕臂，绝缘子，承力索座，套管，定位环；定位装置故障树的最小割集：定位杆，定位管，定位器，定位支座，定位线夹，定位销；支柱与基础故障树的最小割集：支柱，基础。

本文通过最小割集求顶事件发生的概率，表1为我国2011年部分接触网零部件故障统计数据得到的零部件故障率、修复率及故障平均修复时间。

表1 接触网各部件故障统计参数

建立接触网的28跨有限元模型，如图2所示。并在表2所示的12种典型工况下进行仿真。

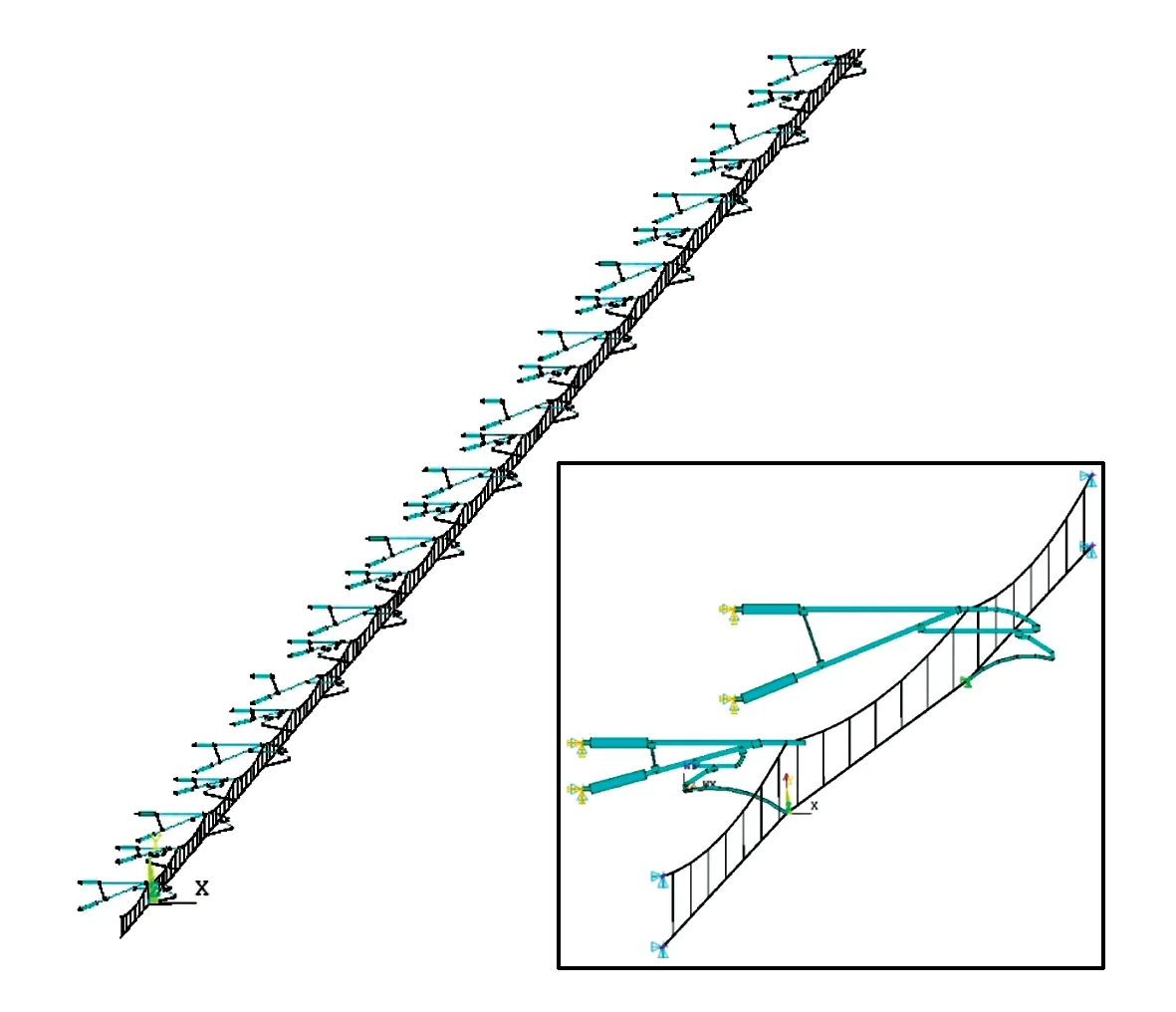
图2 接触网连续28跨有限元模型

速度250260270280290300单弓S250S260S270S280S290S300双弓D250D260D270D280D290D300

在S300工况下仿真得到接触线跨距中点的纵向振动位移最大值为36.66 mm，现场测得接触线中点的最大振动位移为36.24 mm，偏差未超过13%，证明该有限元模型有效。

提取接触网系统仿真环境下各部件的应力时程，如图3为S250、D250两种工况下定位管的应力时程图。计算得到零部件的最大应力值Smax、应力均值Sm1、零均值应力幅值Sa2等，详见表3。

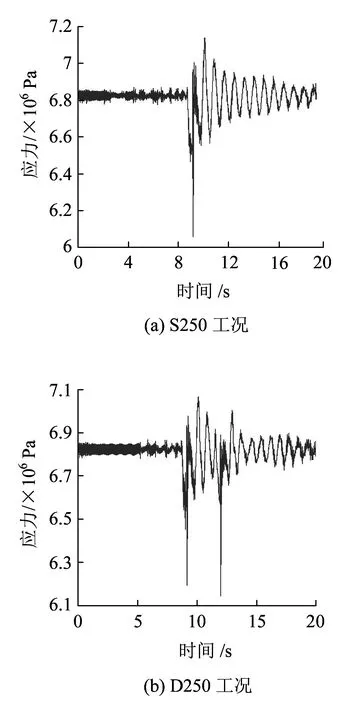
图3 定位管等效应力-时程曲线

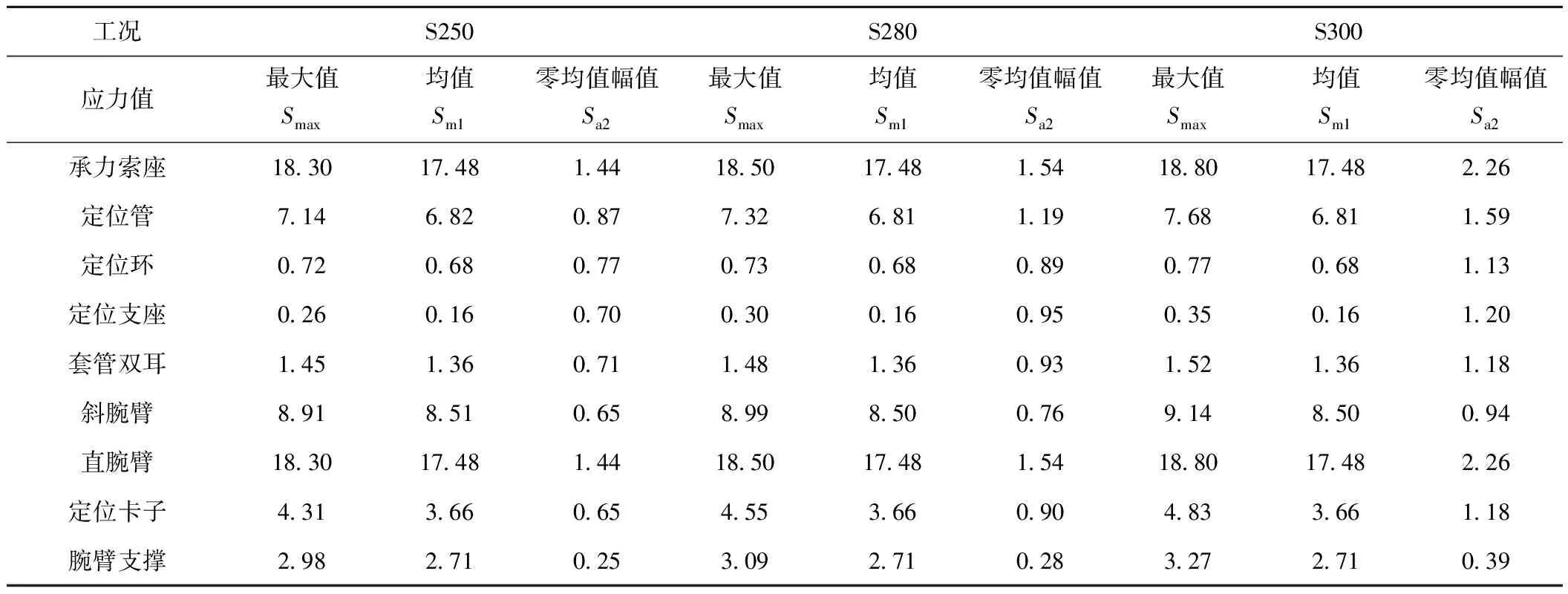
表3 单弓工况应力典型值 单位：MPa

表3所列支持与定位装置中各零部件的材料均为碳素钢Q235A。忽略尺寸系数、表面处理系数及应力集中系数的差别，依据零均值等效载荷的大小对上述零部件进行重要度排序，得到表4。

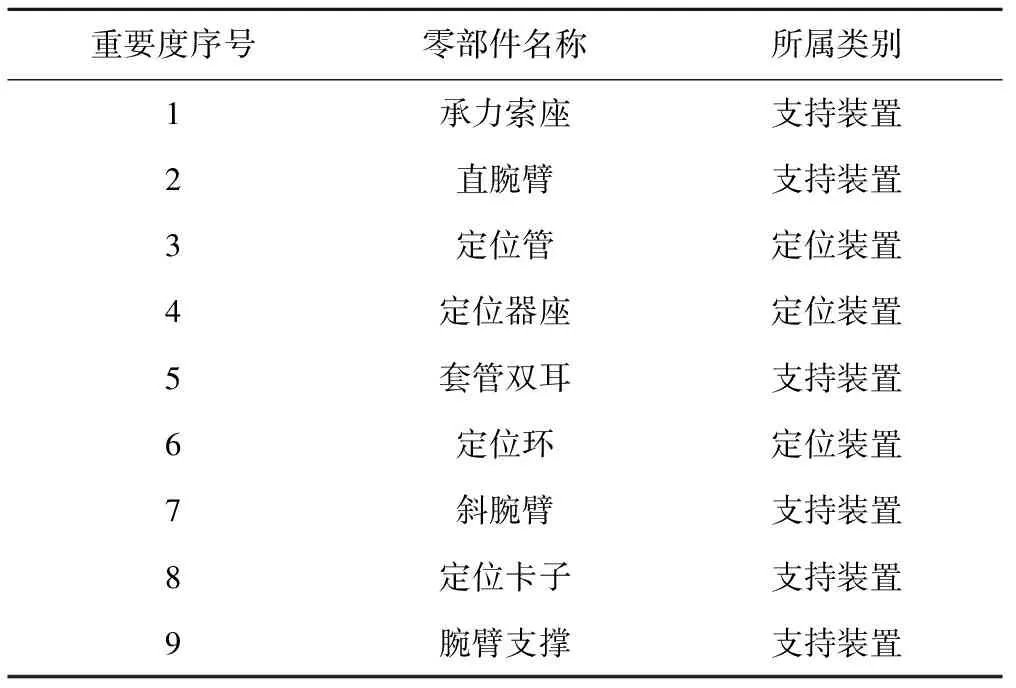
表4 定位-支持装置零部件重要度排序

在实际应用中，定位卡子与定位环在材料、形状、尺寸及表面处理各方面具有高度的相似性，且各典型工况下，定位环的载荷较定位卡子的都大，本文后续只研究定位环。此外，腕臂支撑在各典型工况下的等效载荷均明显小于其他零部件，且在我国2011年部分接触网零部件故障统计数据中也并未提及此零件。因此，腕臂支撑不列为关键零部件。

通过接触网系统故障树模型及仿真环境下各部件的应力时程分析，确定了以定位装置、支持装置为主的直接影响接触网系统运行可靠性的7个关键零部件：定位器支座、定位管、定位环、套管双耳、承力索座、斜腕臂、水平腕臂。

3.2 载荷计数

本文提取列车12种运行工况下的关键零部件节点力时程，截取有效的源数据进行载荷“浓缩”，结合列车行驶工况下测点载荷-时间历程的幅值与均值，定位器支座、定位管、定位卡子和承力索座采用32级，套管双耳、斜腕臂和平腕臂采用16级。

在载荷“浓缩”及载荷分级的基础上，本文针对7个关键零部件的载荷数据采用雨流计数法进行计数，得到了各关键零部件的应力统计谱。本文仅给出定位管在S250工况下的载荷时程曲线及载荷统计直方图，如图4所示。

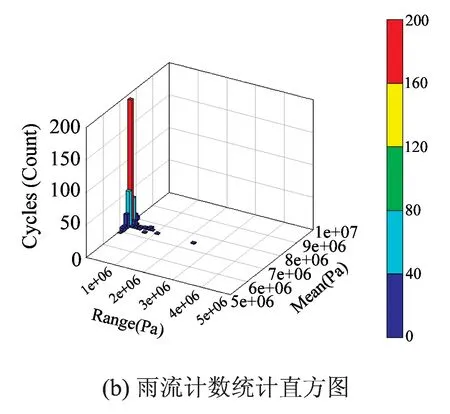
图4 S250工况下定位管应力时程与计数统计

3.3 载荷谱编制

基于上述采用Goodman直线方法得到的零均值载荷，形成可以用于试验加载的块状载荷谱。在各关键零部件疲劳载荷谱编制过程中，剔除了计数统计后各工况下频次均为零的组合。限于篇幅，本文仅给出定位管的疲劳载荷谱，见表5。

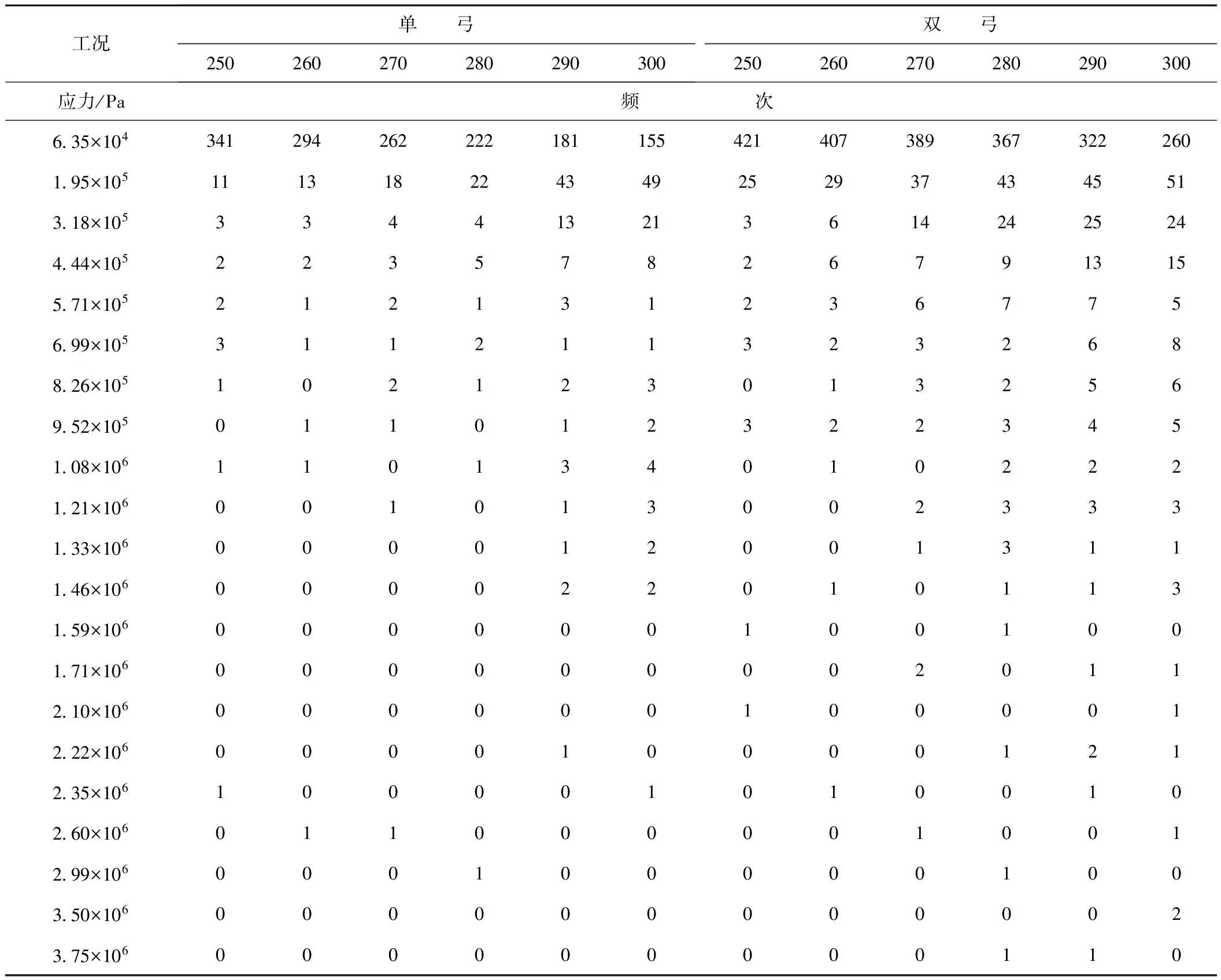
表5 定位管疲劳载荷谱 单位：频次

3.4 结果分析

分析图5(a)可知，当应力值逐渐增大到0.6 MPa时，只有定位管存在相应的频次，故定位管是高速铁路接触网零部件中的薄弱环节。

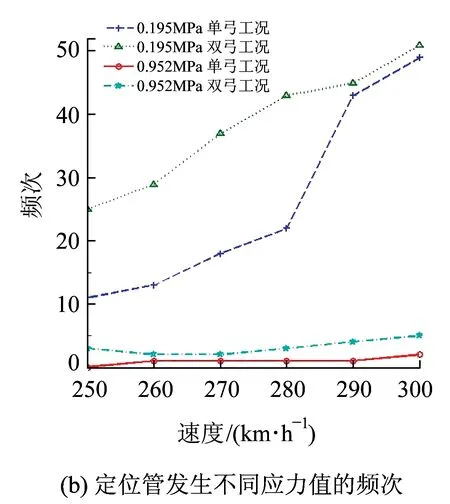
图5 关键零部件载荷谱分析曲线

分析图5(b)可知，对于较小的应力值0.195 MPa，当列车运行速度小于290 km/h时，双弓运行的频次几乎是单弓运行的2倍；当速度大于等于290 km/h时，单双弓运行的频次接近；对于较大应力值0.952 MPa，随着列车运行速度增加，双弓运行与单弓运行发生的频次差距逐渐增大。因此当运行速度增加到290 km/h时，双弓运行产生的疲劳破坏明显增加。

4 结论

本文基于接触网故障树模型与有限元动力仿真分析得到接触网系统的7个关键零部件：定位器支座、定位管、定位环、套管双耳、承力索座、斜腕臂、水平腕臂，编制了块状疲劳载荷谱。分析载荷谱结果表明，当运行速度增加到290 km/h时，双弓运行产生的疲劳破坏明显增加；定位管是高铁接触网零部件中的薄弱环节。

参考文献：

[1]MASSAT J P,NGUYEN-TAJAN T M L.Fatigue Analysis of Catenary Contact Wires for High Speed Trains[J].9 th World Congress on Railway Research,2011.

[2]POMMIER,SYLVIE.Extended Finite Element Method for Crack Propagation[M].United States:Iste,2013.

[3]BON H K,JUN M C.Reliability Assessment of Catenary of Electric Railway by Using FTA and ETA Analysis[J].Environment and Electrical Engineering(EEEIC),2011 10th International Conference,2011.

[4]罗松松.接触网系统可靠性与维修性研究[D].成都：西南交通大学，2008.

[5]何巨东,李会杰,邓斌,等.基于应力-强度干涉理论的接触网零部件可靠性计算[J].机械研究与应用，2008，21(2):83-85.

HE Ju-dong,LI Hui-jie,DENG Bin,et al.Reliability Calculation of Catenary Parts basecl on the Stress-strength Theory[J].Mechanical Research and Application,2008,21(2):83-85.

[6]刘莉娜.电气化铁道接触网抱箍类零部件有限元分析[D].天津：天津大学,2004.

[7]李鹏.弓-网耦合系统的动态模拟及疲劳分析[D].天津：天津大学，2009.

[8]彭再恒.应用TCL/TK语言对弓网耦合系统的界面开发及相关疲劳分析[D].天津：天津大学，2009.

[9]MASSAT J P,LAINE J P,BOBILLOT A.Pantograph-catenary Dynamics Simulation[J].Vehicle System Dynamics:2007,44(S):551-559.

[10]魏喆.高速铁路接触网支持悬挂系统的动态特性研究[D].武汉：武汉大学，2011.

[11]戚广枫.高速铁路接触网安全可靠性及可维修性研究[M].成都：西南交通大学出版社,2012.